As an object is moved from the surface of a thin converging lens to a focal point, over what range does the image distance very?
The correct Answer is:A, B, C, D
To solve the problem of how the image distance varies as an object is moved from the surface of a thin converging lens to its focal point, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula is given by:
1v−1u=1f
where:
- v is the image distance,
- u is the object distance (with a negative sign for real objects),
- f is the focal length of the lens.
Step 2: Case 1 - Object at the Surface of the Lens
When the object is at the surface of the lens, we can consider the object distance u to be 0 (since the surface of the lens is our reference point). Substituting u=0 into the lens formula:
1v−10=1f
This simplifies to:
1v=1f
Thus, we find:
v=0
This means that the image is formed at the lens itself when the object is at the surface.
Step 3: Case 2 - Object at the Focal Point
Next, we consider the case when the object is at the focal point of the lens. Here, the object distance u is equal to −f (the negative sign indicates that the object is on the same side as the incoming light). Substituting u=−f into the lens formula:
1v−1−f=1f
This simplifies to:
1v+1f=1f
Rearranging gives:
1v=0
Thus, we find:
v=∞
This means that when the object is at the focal point, the image is formed at infinity.
Step 4: Conclusion
From the two cases analyzed:
- When the object is at the surface of the lens, the image distance v is 0.
- When the object is at the focal point, the image distance v approaches infinity.
Thus, we conclude that as the object moves from the surface of the lens to the focal point, the image distance varies from 0 to ∞.
Final Answer
The image distance varies from 0 to ∞.
---
The lens formula is given by:
1v−1u=1f
where:
- v is the image distance,
- u is the object distance (with a negative sign for real objects),
- f is the focal length of the lens.
When the object is at the surface of the lens, we can consider the object distance u to be 0 (since the surface of the lens is our reference point). Substituting u=0 into the lens formula:
1v−10=1f
This simplifies to:
1v=1f
Thus, we find:
v=0
This means that the image is formed at the lens itself when the object is at the surface.
Next, we consider the case when the object is at the focal point of the lens. Here, the object distance u is equal to −f (the negative sign indicates that the object is on the same side as the incoming light). Substituting u=−f into the lens formula:
1v−1−f=1f
This simplifies to:
1v+1f=1f
Rearranging gives:
1v=0
Thus, we find:
v=∞
This means that when the object is at the focal point, the image is formed at infinity.
From the two cases analyzed:
- When the object is at the surface of the lens, the image distance v is 0.
- When the object is at the focal point, the image distance v approaches infinity.
The image distance varies from 0 to ∞.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.7
Explore 2 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.8
Explore 8 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.5
Explore 5 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionA point object O moves from the principal axis of a converging lens in a direction OP. I is the image of O, will move initially in the direction
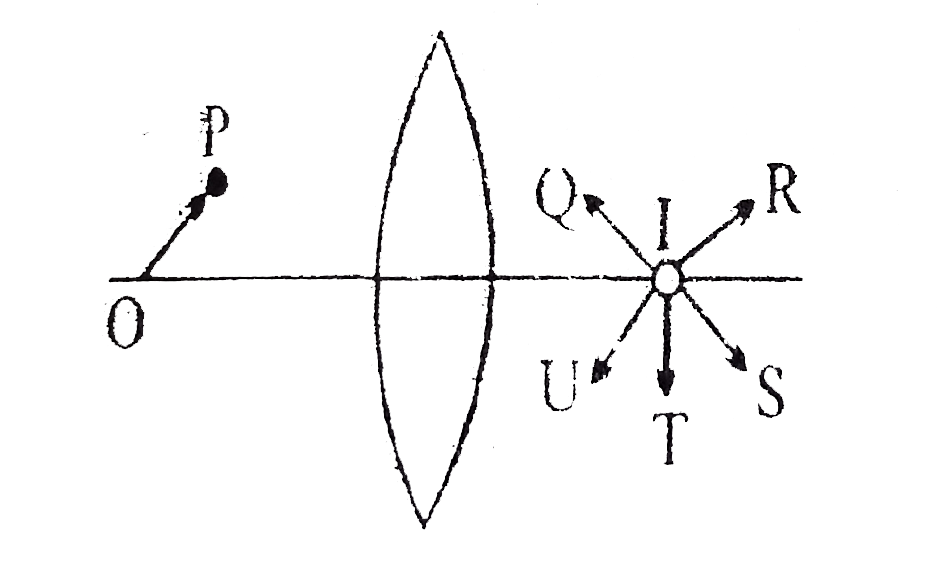
View SolutionAn object is placed 12cm to the left of a converging lens of focal length 8cm. Another converging lens of 6cm focal lengh is placed at a distance of 30cm to the right of the first lens. The second lens will produce
View SolutionChoose the correct alternative corresponding to the object distance 'u', image distance 'v' and the focal length 'F' of a converging lens from the following .
(i) The average speed of the image as the object moves with the uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with same speed from distance F2toF4
(ii) The minimum distance between a real object and its real image in case of a converging lens is 4F where F is its focal length.
View SolutionThe image of the moon is focused by a converging lens of focal length 50 cm on a plane screen. The image is seen by an unaided eye from a distance of 25 cm. Find the angular magnification achieved due to the converging lens.
View SolutionA point source of light is placed inside water and a thin converging lens of focal length f is placed just outside the surface of water. The image of source is formed at a distance of 50 cm from the surface of water. When the lens is placed just inside the water surface the image is formed at a distance of 40 cm from the surface of water. if focal length of the lens in air is f=100k8 cm, then find the value of k. (given refractive index of lens is 3/2 and that of water is 4/3 and in both cases image is formed inside water for the viewer in air).
View SolutionAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionAn object is placed in front of a converging lens at a distance equal to twice the focal length f1 of the lens. On the other side of the lens is a concave mirror of focal length f2 separated from the lens is a concave mirror of focal length f2 separated from the lens by a distance 2(f1+f2). Light from the object passes rightward through the lens, reflects from the mirror, passes leftward throught the lens, and forms a final image of the object.

View SolutionAn object is gradually moving away from the focal point of a converging lens along the axis of the lens. The graphical representation of the magnitude of linear magnification (m) versus distance of the object from the lens (x) is correctly given by : (Graphs are drawn schematically and are not to scale)
View Solution