Show that the focal length of a thin lens is not changed when the lens is rotated so that the left and the right surfaces are interchanged.
The correct Answer is:A
To show that the focal length of a thin lens does not change when the lens is rotated such that the left and right surfaces are interchanged, we can follow these steps:
1. Define the Lens and Surfaces:
Consider a thin lens with two surfaces. Let the first surface be denoted as R1 and the second surface as R2. The lens has a refractive index μ.
2. Apply the Lensmaker's Formula:
The Lensmaker's formula relates the focal length f of a lens to its radii of curvature and the refractive index. For the original orientation of the lens, the formula is given by:
1f1=(μ−1)(1R1−1R2)
Here, f1 is the focal length when light comes from the side of R1.
3. Interchange the Surfaces:
When the lens is rotated, the surfaces are interchanged. Now, the first surface becomes R2 and the second surface becomes R1. The new focal length f2 can be expressed as:
1f2=(μ−1)(1R2−1R1)
4. Simplify the New Expression:
Notice that the expression for f2 can be rewritten:
1f2=(μ−1)(1R2−1R1)=(μ−1)(−(1R1−1R2))
This shows that:
1f2=−(μ−1)(1R1−1R2)
5. Relate f1 and f2:
From the original expression for f1, we have:
1f1=(μ−1)(1R1−1R2)
Therefore, we can see that:
1f2=−1f1
This implies that f1=f2.
6. Conclusion:
Since f1=f2, we conclude that the focal length of the thin lens does not change when the lens is rotated such that the left and right surfaces are interchanged.
Consider a thin lens with two surfaces. Let the first surface be denoted as R1 and the second surface as R2. The lens has a refractive index μ.
The Lensmaker's formula relates the focal length f of a lens to its radii of curvature and the refractive index. For the original orientation of the lens, the formula is given by:
1f1=(μ−1)(1R1−1R2)
Here, f1 is the focal length when light comes from the side of R1.
When the lens is rotated, the surfaces are interchanged. Now, the first surface becomes R2 and the second surface becomes R1. The new focal length f2 can be expressed as:
1f2=(μ−1)(1R2−1R1)
Notice that the expression for f2 can be rewritten:
1f2=(μ−1)(1R2−1R1)=(μ−1)(−(1R1−1R2))
This shows that:
1f2=−(μ−1)(1R1−1R2)
From the original expression for f1, we have:
1f1=(μ−1)(1R1−1R2)
Therefore, we can see that:
1f2=−1f1
This implies that f1=f2.
Since f1=f2, we conclude that the focal length of the thin lens does not change when the lens is rotated such that the left and right surfaces are interchanged.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.7
2 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.8
8 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.5
5 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Find the focal length of the lens used.
View SolutionThe focal length of the eye lens increases when eye muscles
View SolutionA change in the focal length of the eye lens is brought by.
View SolutionThe change in focal length of an eye lens is caused by the action of the
View SolutionA focal length of a lens 10cm. What is power of a lens in dipotre?
View SolutionRadius of curvature of first surface of double convex lens is three times that of the other. If focal length of the lens is 30 cm and refractive index of the lens is 3/2, then radius of curvature of the first surface is
View SolutionThe focal length of a plano-concave lens is -10 cm , then its focal length when its palne surface is polished is
View SolutionCalculate the focal length of the thin lens shown infigure. The pionts C1andC2 denote the centres of curvature.
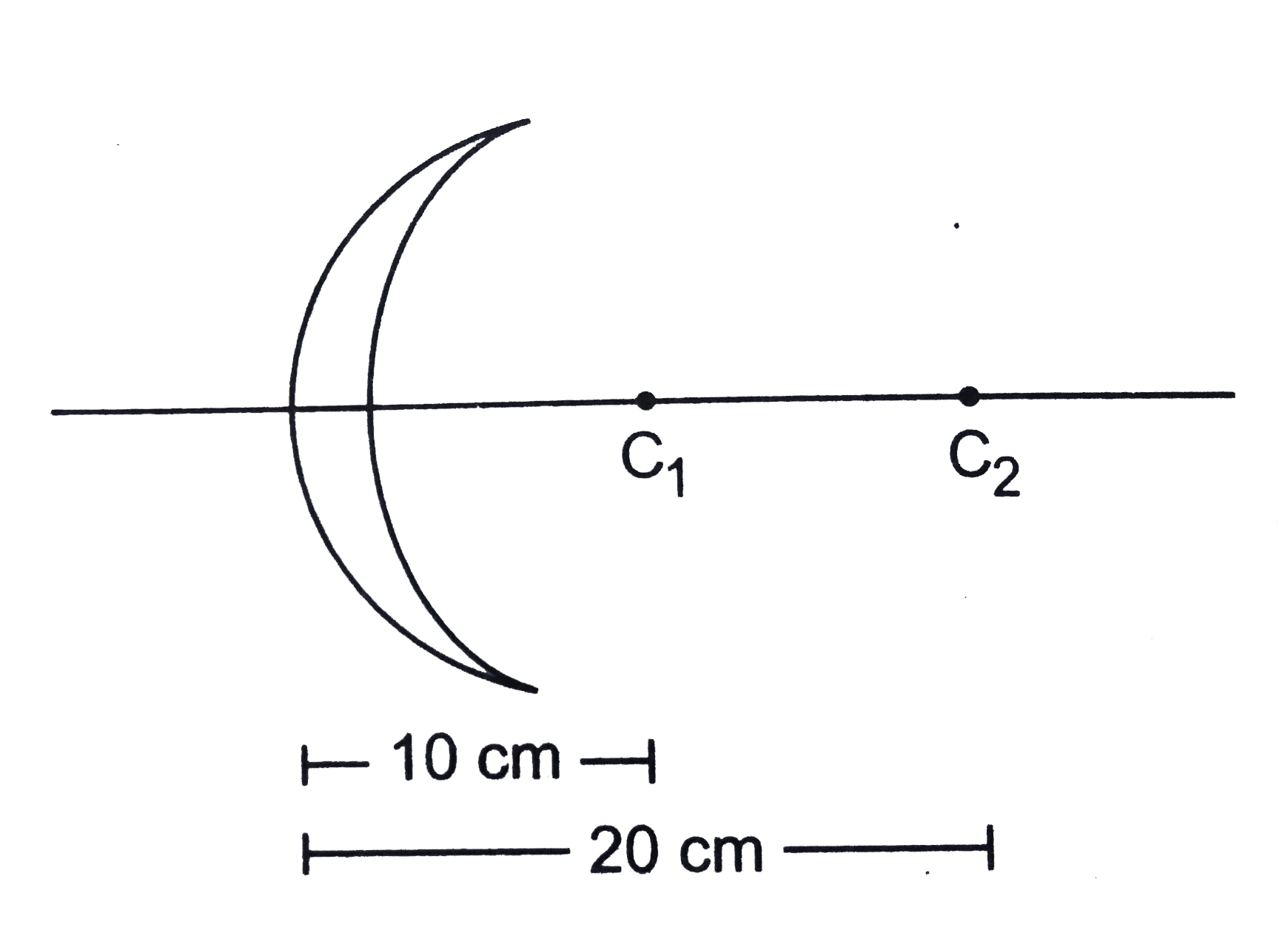
View SolutionIf a thin lens is dipped in water, does its focal length change ?
View SolutionThe focal length of a thin convex-lens is 30cm. At a distance of 10 cm from the lens there is a plane refracting surface fo refractive inidex 3/2 Where will parallel rays incident on lens converge?

View Solution
