Suppose an object has thickness du so that it extends from object distance u to u+du. Prove that the thickness dv of its image is given by (−v2u2)du, so the longitudinal magnification dvdu=−m2, where m is the lateral magnification.
The correct Answer is:A
To solve the problem, we need to prove that the thickness dv of the image is given by
dv=−v2u2du
and that the longitudinal magnification dvdu=−m2, where m is the lateral magnification.
1. Understand the Lens Formula:
The lens formula is given by
1f=1v−1u
where f is the focal length, v is the image distance, and u is the object distance.
2. Differentiate the Lens Formula:
Since f is a constant, differentiating both sides with respect to u gives:
0=−d(v−1)du+d(u−1)du
This can be rewritten as:
0=−(−1v2dv)+(−1u2du)
Simplifying this, we have:
0=dvv2−duu2
3. Rearranging the Equation:
Rearranging gives:
dvv2=duu2
Multiplying both sides by v2 and u2:
dv=−v2u2du
Here, we introduce a negative sign because the image distance v is considered negative in the context of real images formed by converging lenses.
4. Longitudinal Magnification:
The longitudinal magnification ML is defined as:
ML=dvdu
Substituting our expression for dv:
ML=−v2u2dudu=−v2u2
Since the lateral magnification m is defined as:
m=h′h=vu
We can express ML in terms of m:
ML=−m2
5. Conclusion:
Thus, we have shown that:
dv=−v2u2du
and
dvdu=−m2
The lens formula is given by
Since f is a constant, differentiating both sides with respect to u gives:
Rearranging gives:
The longitudinal magnification ML is defined as:
Thus, we have shown that:
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.7
Explore 2 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.8
Explore 8 Videos
- REFRACTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFRACTION OF LIGHTExercise:Exercise 31.5
Explore 5 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
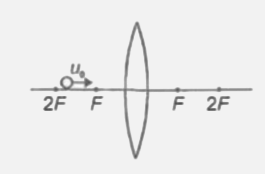
A point object is moving with speed u0 at a position somewhere between 2F and F in front of a convex lens. The speed of its image is
View SolutionWhen the object is at distance u1andu2 from the optical centre of a convex lens, a real and a virtual image of the same magnification are obtained. The focal length of the lens is
View Solution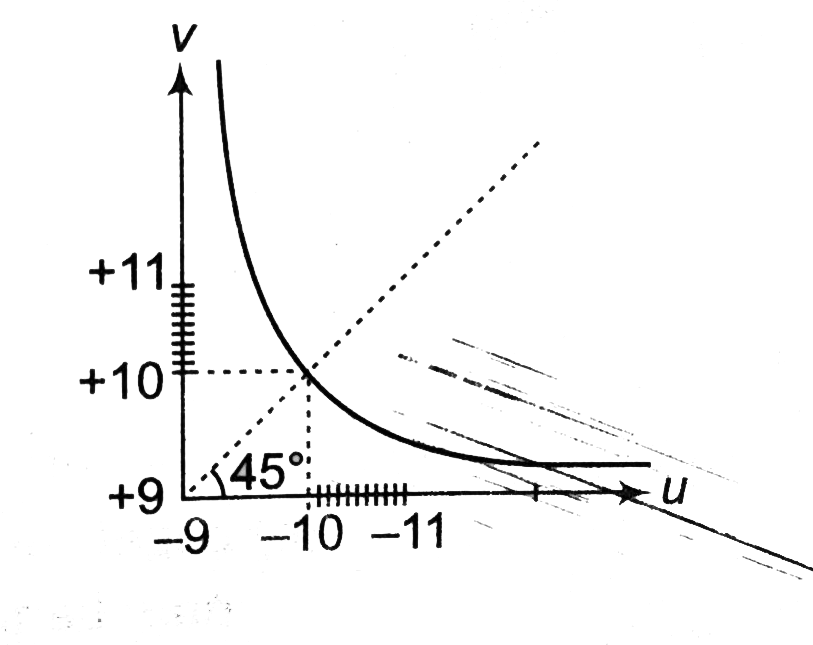 .
.
The graph between object distance u and image distance v from a convex lens is given .The correct option option , from the following ,is
View SolutionChoose the correct alternative corresponding to the object distance 'u', image distance 'v' and the focal length 'F' of a converging lens from the following .
(i) The average speed of the image as the object moves with the uniform speed from distance 3F4 to F2 is greater than the average speed of the image as the object moves with same speed from distance F2toF4
(ii) The minimum distance between a real object and its real image in case of a converging lens is 4F where F is its focal length.
View SolutionTwo thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
View SolutionTwo thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
View SolutionTwo thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
View SolutionA compound microscope has objective of focal length 3.2 mm and eyepiece of 12 mm focal length. If the objective forms image of the object 16 cm beyond its pole, then total magnification achieved is
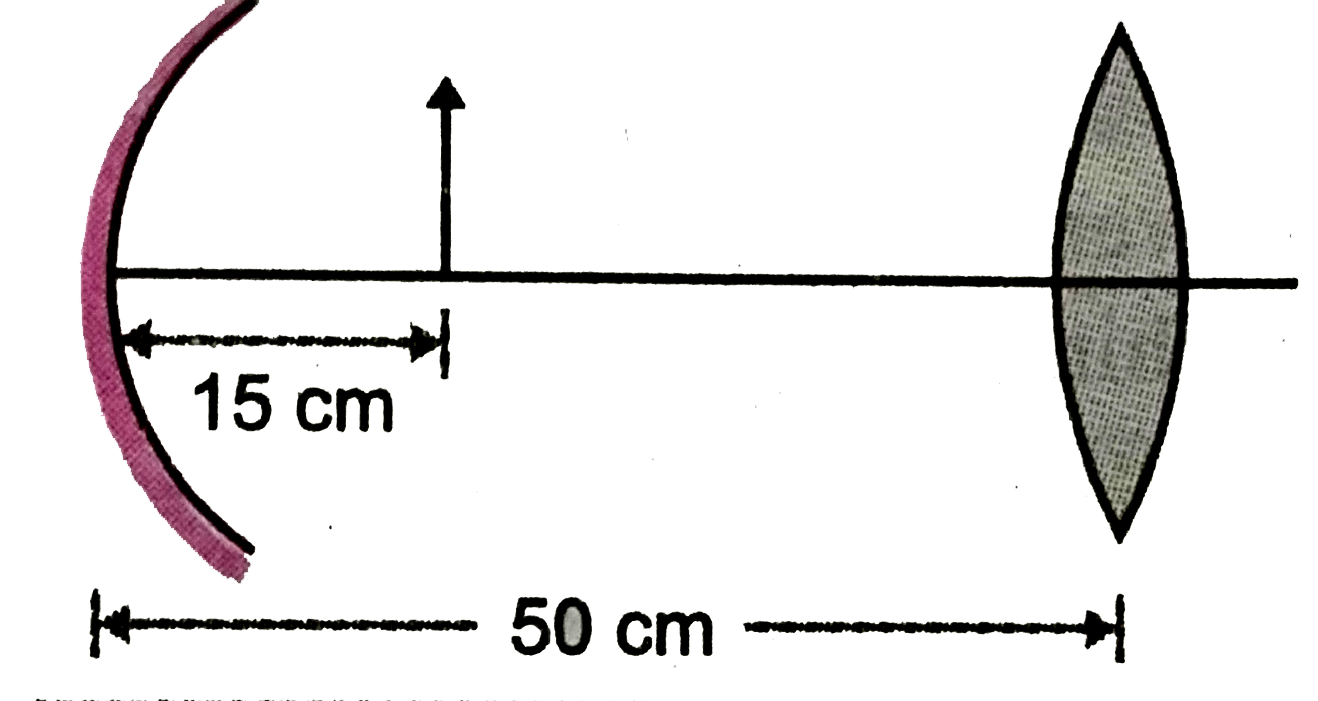
View SolutionConsider a concave mirror and a convex lens (refractive index 1.5) of focal length 10cm each separated by a distance of 50cm in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of 15cm from the mirror. Its erect image formed by this combination has magnification M1. When this set up is kept in a medium of refractive index 7/6, the magnification becomes M2. The magnitude (M2M1) is :
 .
.
View SolutionA short linear object is placed at a distance u along the axis of a spherical mirror of focal length f.
a. Obtain an expression for the longitudinal magnification.
b. Also, obtain an expression for th eration of the velocity of image (v) to the velocity of the object (u).
View Solution

