Calculate the focal length of the thin lens shown infigure. The pionts C1andC2 denote the centres of curvature.
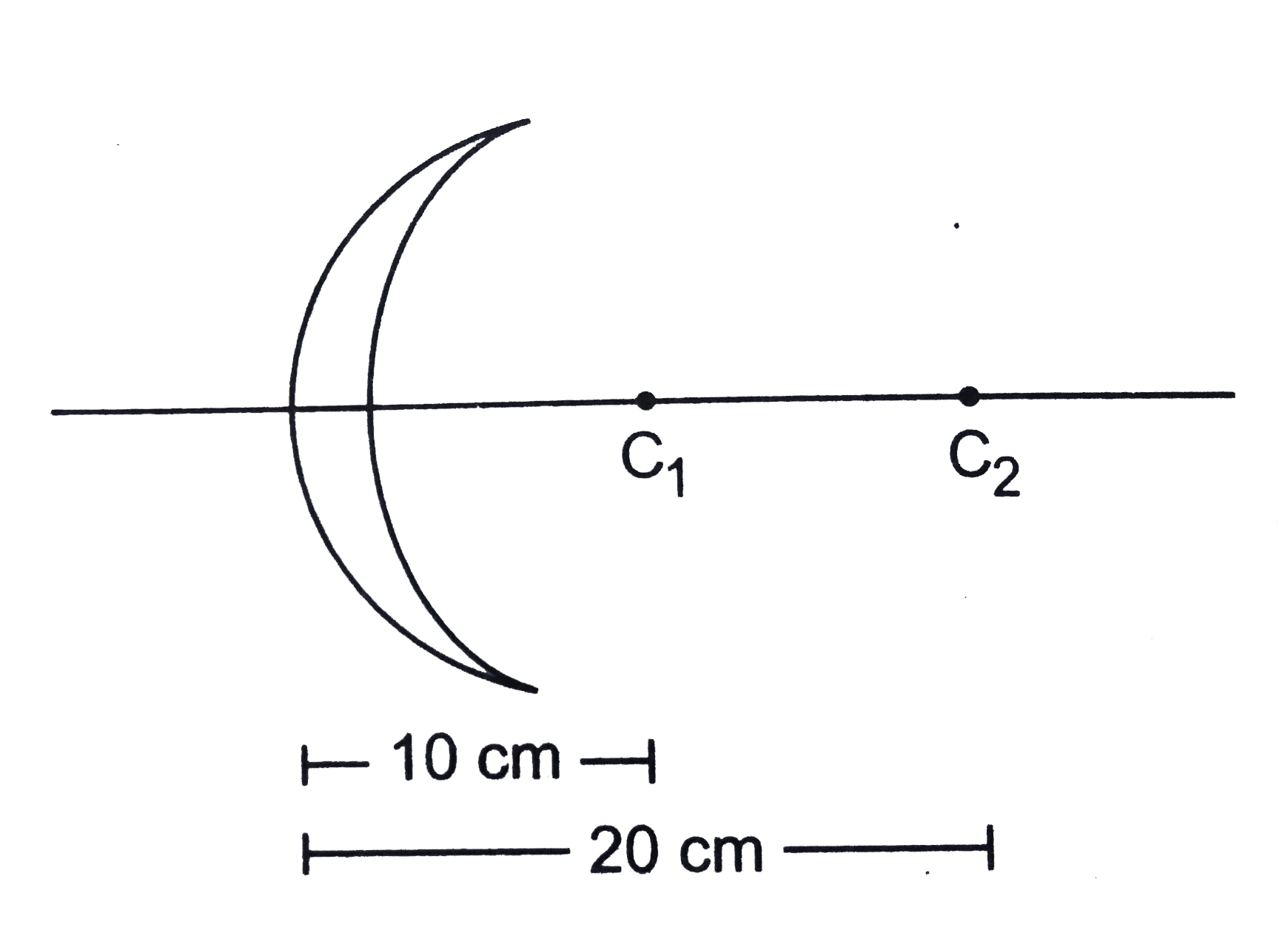
As is clear from the ure boththe radii of curvature are positive. Thus, R1=+10cm and R2=+20cm. The focal length is given by
1f=(μ−1)(1R1−1R2)
=(1.5−1)(110cm−120cm)
=0.5×120cm=140cm
orf=40cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -1
15 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
Find the focal length of the lens shown in Fig.
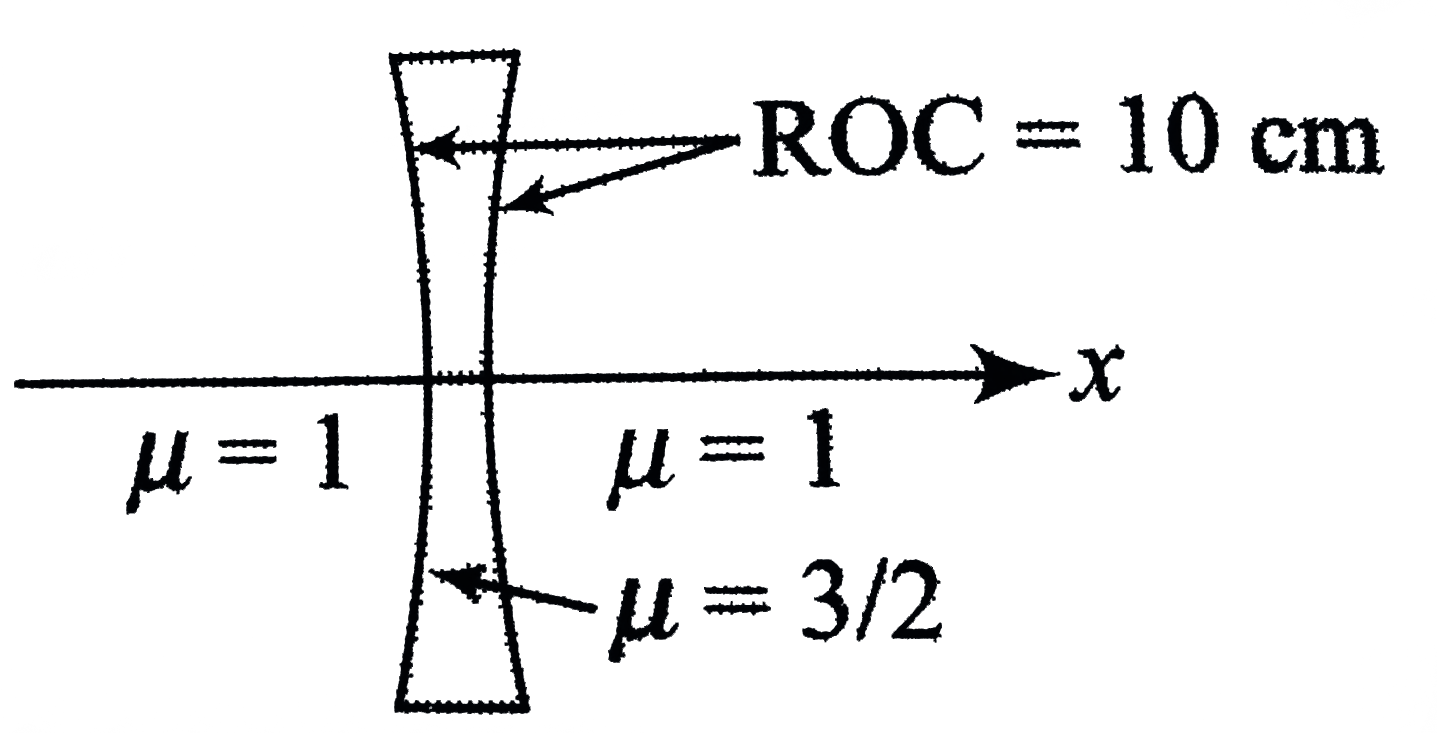
View SolutionFind the focal length of the lens shown in the Fig..
View SolutionLocate the image of the point object O in the situation shown in figure. The point C denotes the centre of curvature of the separating surface.

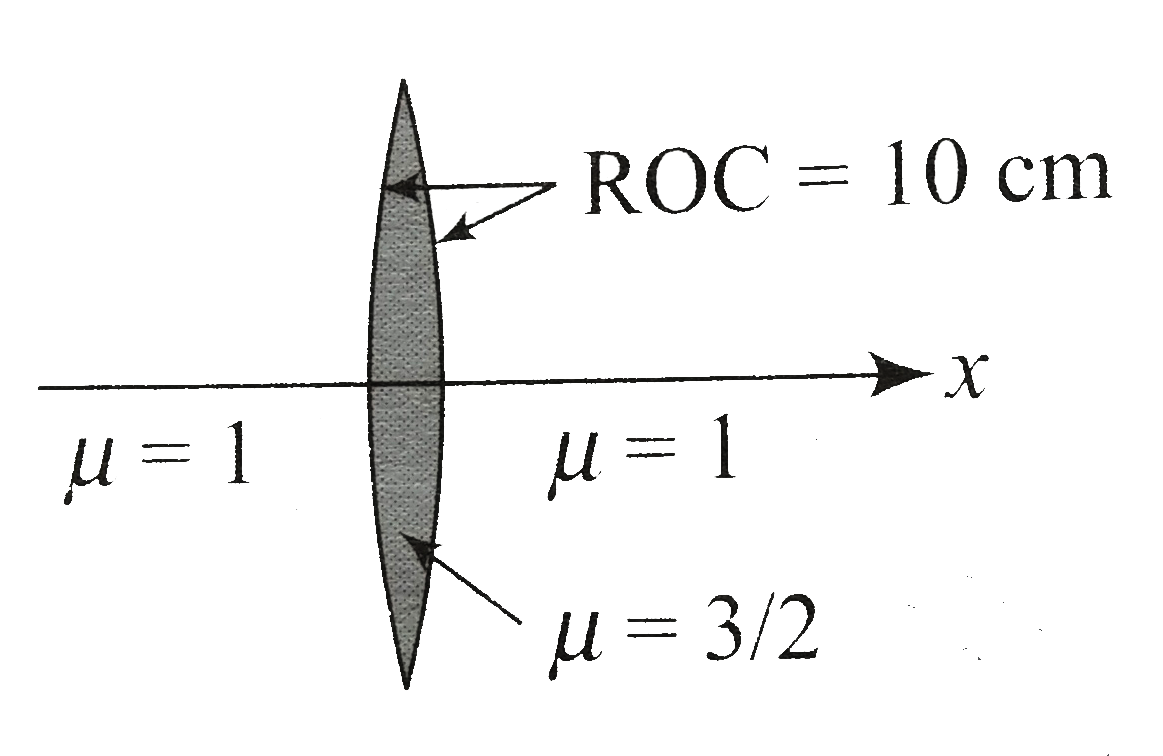
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
View SolutionCalculate focal length of given lens if the magnification is −0.5.
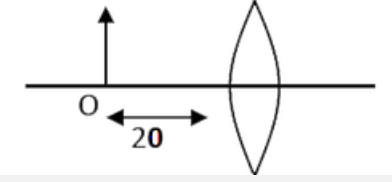
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
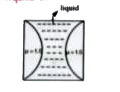
View SolutionRadius of curvature of first surface of double convex lens is three times that of the other. If focal length of the lens is 30 cm and refractive index of the lens is 3/2, then radius of curvature of the first surface is
View SolutionShow that the focal length of a thin lens is not changed when the lens is rotated so that the left and the right surfaces are interchanged.
View SolutionA thin glass lens of refractive index μ2=1.5 behaves as an interface between two media of refractive indices μ1=1.4andμ3=1.6 respectively. Determine the focal length of the lens for the shown arrangement of radius of curvature of both surfaces 20cm.
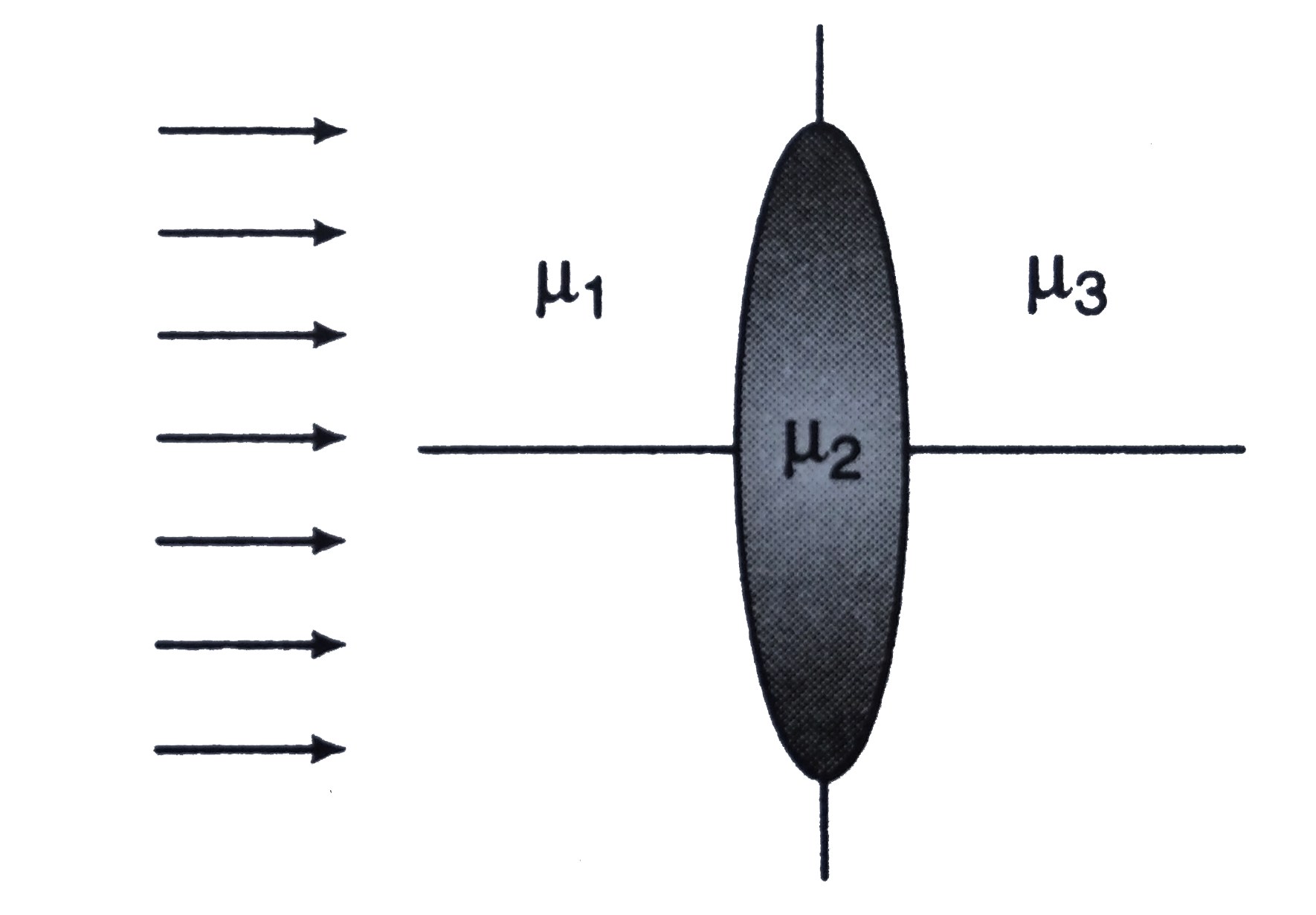
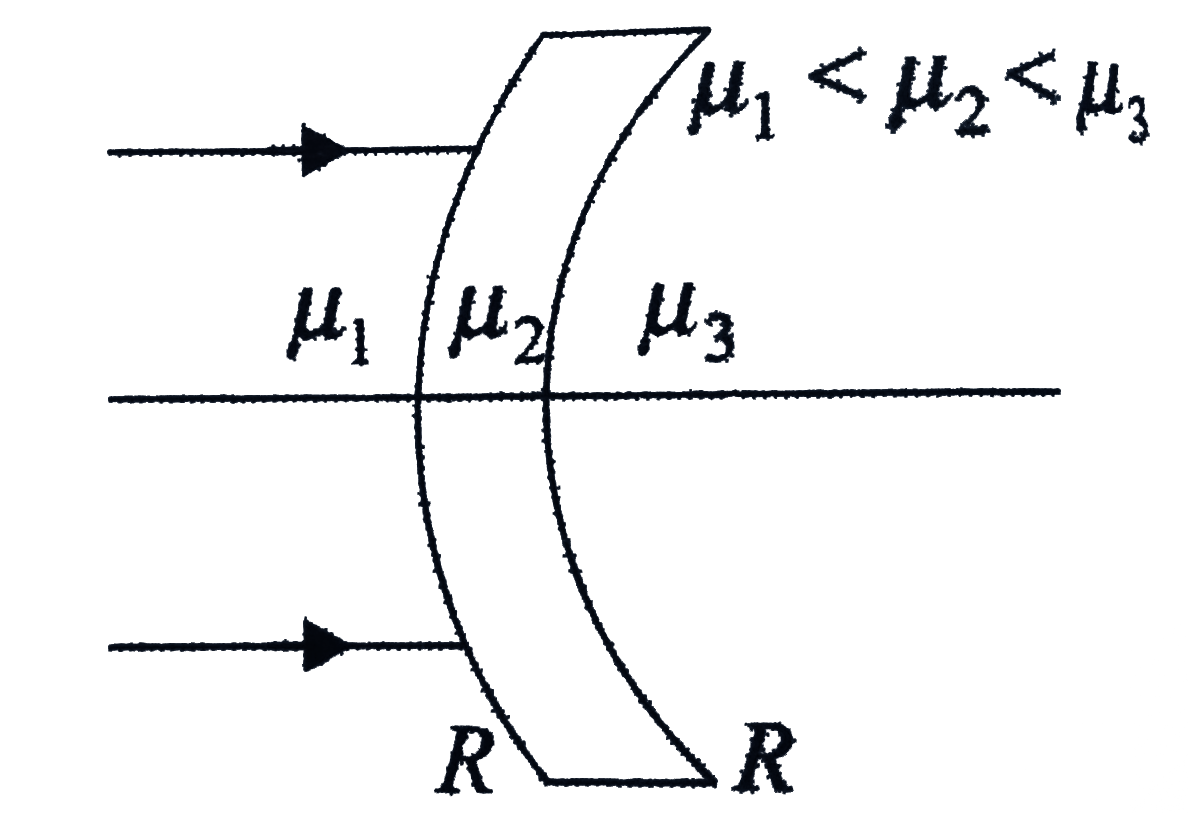
View SolutionLight is incident on the thin lens as shown in figure. The refractive index of the material of the lens is μ2. The radii of curvature of both the surfaces are R. The refractive index of the medium of left side is μ1, while that of right side is μ3. What is the focal length of the lens?

View Solution
