Question

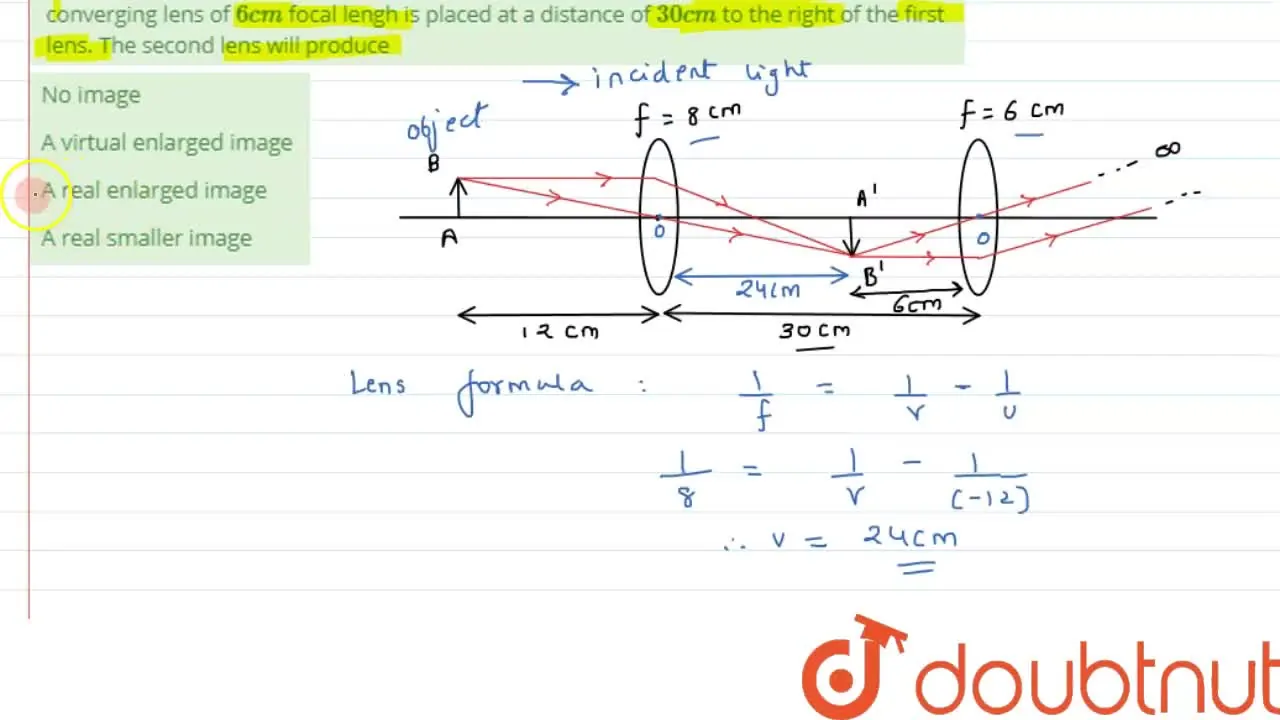
An object is placed $12cm$ to the left of a converging lens of focal length $8cm$. Another converging lens of $6cm$ focal lengh is placed at a distance of $30cm$ to the right of the first lens. The second lens will produce

Options

A. No image
B. A virtual enlarged image
C. A real enlarged image
D. A real smaller image

Answer

3

Explanation

To solve the problem step by step, we will use the lens formula and the information given about the two converging lenses.

Step 1: Identify the parameters for the first lens
- Focal length (f1) of the first lens = +8 cm (positive for converging lens)
- Object distance (u1) for the first lens = -12 cm (negative as the object is on the left side)

Step 2: Use the lens formula for the first lens
The lens formula is given by:
\( \frac{1}{f} = \frac{1}{v} - \frac{1}{u} \)
Rearranging gives:
\( \frac{1}{v} = \frac{1}{f} + \frac{1}{u} \)

Substituting the values:
\( \frac{1}{v_1} = \frac{1}{8} + \frac{1}{-12} \)

Step 3: Calculate the image distance (v1) for the first lens
Finding a common denominator (24):
\( \frac{1}{v_1} = \frac{3}{24} - \frac{2}{24} = \frac{1}{24} \)
Thus,
\( v_1 = 24 \text{ cm} \)

Step 4: Determine the position of the first image
The first image (B') is formed 24 cm to the right of the first lens. Since the distance between the two lenses is 30 cm, the distance from the first image to the second lens is:
\( 30 \text{ cm} - 24 \text{ cm} = 6 \text{ cm} \)

Step 5: Identify the parameters for the second lens
- Focal length (f2) of the second lens = +6 cm
- Object distance (u2) for the second lens = -6 cm (since the first image is on the left side of the second lens)

Step 6: Use the lens formula for the second lens
Using the lens formula again:
\( \frac{1}{v_2} = \frac{1}{f_2} + \frac{1}{u_2} \)

Substituting the values:
\( \frac{1}{v_2} = \frac{1}{6} + \frac{1}{-6} = \frac{1}{6} - \frac{1}{6} = 0 \)

Step 7: Interpret the result for the second lens
Since \( \frac{1}{v_2} = 0 \), this implies that \( v_2 \) is at infinity. Therefore, the second lens produces an image at infinity.

Step 8: Determine the nature of the image
Since the image is formed at infinity, it will be:
- Real (as it is formed on the opposite side of the lens)
- Enlarged (as images at infinity are typically considered to be enlarged)

Final Answer
The second lens will produce a real and enlarged image.

---