A parallel beam of light enters a clear plastic bead 2.50cm in diameter and index 1.44. At what point beyond the bead are these rays brought to a focus?
The correct Answer is:C, D
To solve the problem of finding the point beyond the bead where the rays of light are brought to a focus, we can use the lens maker's formula for refraction at a spherical surface. Here’s a step-by-step solution:
Step 1: Identify Given Values
- Diameter of the bead (d) = 2.50 cm
- Radius of the bead (R) = d/2 = 2.50 cm / 2 = 1.25 cm
- Refractive index of the bead (μ2) = 1.44
- Refractive index of air (μ1) = 1.00
- Object distance (u) = ∞ (since the light rays are parallel)
Step 2: Use the Refraction Formula
The refraction formula for a spherical surface is given by:
μ2V−μ1u=μ2−μ1R
Step 3: Substitute the Known Values
Substituting the known values into the formula:
1.44V−1.00∞=1.44−1.001.25
Since 1.00∞=0, we can simplify this to:
1.44V=0.441.25
Step 4: Solve for V
Now, we can rearrange the equation to solve for V:
V=1.44×1.250.44
Calculating the right-hand side:
V=1.800.44≈4.09 cm
Final Answer
The rays are brought to a focus approximately 4.09 cm beyond the bead.
---
- Diameter of the bead (d) = 2.50 cm
- Radius of the bead (R) = d/2 = 2.50 cm / 2 = 1.25 cm
- Refractive index of the bead (μ2) = 1.44
- Refractive index of air (μ1) = 1.00
- Object distance (u) = ∞ (since the light rays are parallel)
The refraction formula for a spherical surface is given by:
Substituting the known values into the formula:
Now, we can rearrange the equation to solve for V:
The rays are brought to a focus approximately 4.09 cm beyond the bead.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.6
12 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.7
2 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.4
1 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A convex lens of diameter 8.0 cm is used to focus a parallel beam of light of wavelength 620 nm. If the light be focused at a distance of 20 cm from the lens, what would be the radius of the central bright spot formed ?
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View SolutionA ray of light falls normally on a rectangular glass slab.
Draw a ray diagram showing the path of the ray till it emerges out of the slab.
View SolutionA slightly divergent beam of charged particles accelerated by a Potential difference V propogates from a point A along the axis of a solenoid. The beam is brought into focus at a distance l from the point A at two successive values of magnetic induction B1andB2. Find the specific charge q/m of the particles.
View SolutionTwo parallel beams of light P and Q are incident normally on a prism and the transmitted rays are brought to focus with the help of a convergent lens as shown in Fig. 2.23. If the intensities of the upper and lower beams immediately after transmission from face AC are 4I abd I, respectively, find the resultant intensity at the focus.
View SolutionA parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6cm and refractive index 1.5, placed in air as shown in figure (i). Assume paraxial ray approxiamtion.
 .
.
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
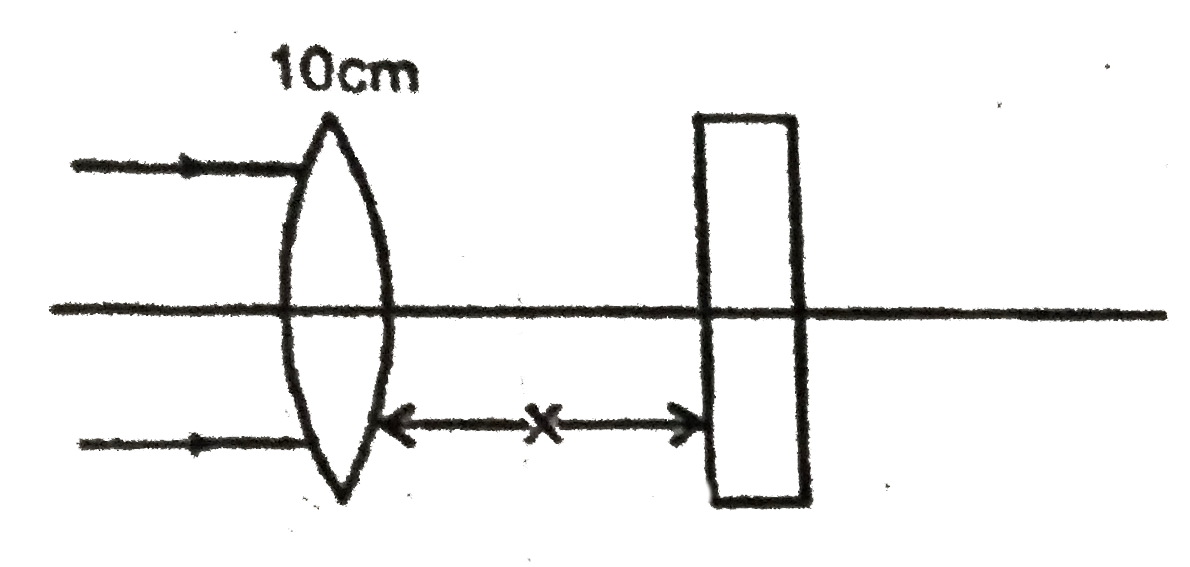
View SolutionA parallel beam of light is incident on a lens of focal length 10cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. The nature of the final image from the lens slab combination is: (Assume rays paraxial)
View SolutionSTATEMENT -1: A white parallel beam of light is incident on a plane glass-vacuum interface as shown. The beam may not undergo dispesion after suffering deviation at the interface (The beam is not incident normally on the interface.)

STATEMENT -2: Vacuum has same refractive index for all colours of white light.
View SolutionA parallel beam of light falls on the surface of a convex lens whose radius of curvature of both sides of 20cm. The refractive index of the material of the lens varies as μ=1.5+0.5r , where r is the distance of the point on the aperture from the optical centre in cm. Find the length of the region on the axis of the lens where the light will appear. The radius of aperture of the lens is 1cm.
View Solution
