Assertion: A charged particle enters in a magnetic field B=B0ˆiwithvelocityv=v0ˆi+v0ˆj, then minimum speed of charged particle may be v0.
Reason: A variable acceleration particle may be v0.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:D
To solve the question, we need to analyze both the assertion and the reason provided.
Step 1: Analyze the Assertion
The assertion states that a charged particle enters a magnetic field with a velocity →v=v0^i+v0^j and the minimum speed of the charged particle may be v0.
1. Calculate the Magnitude of Velocity:
The magnitude of the velocity →v can be calculated using the Pythagorean theorem:
|→v|=√(v0)2+(v0)2=√2v20=v0√2
This shows that the speed of the particle is v0√2, which is greater than v0.
2. Conclusion about Assertion:
Since the minimum speed of the charged particle cannot be v0 (it is actually v0√2), the assertion is false.
Step 2: Analyze the Reason
The reason states that a variable acceleration particle may be v0.
1. Understanding Variable Acceleration:
A charged particle moving in a magnetic field experiences a centripetal force that changes the direction of its velocity, leading to variable acceleration. The speed of the particle remains constant, but the direction changes, resulting in variable acceleration.
2. Conclusion about Reason:
The statement that a variable acceleration particle may have a speed of v0 is true because the particle can indeed have a constant speed while experiencing variable acceleration due to the change in direction.
Final Conclusion
- The assertion is false.
- The reason is true.
Summary of the Solution
- Assertion: False (minimum speed is v0√2).
- Reason: True (a charged particle can have constant speed while experiencing variable acceleration).
The assertion states that a charged particle enters a magnetic field with a velocity →v=v0^i+v0^j and the minimum speed of the charged particle may be v0.
The magnitude of the velocity →v can be calculated using the Pythagorean theorem:
|→v|=√(v0)2+(v0)2=√2v20=v0√2
This shows that the speed of the particle is v0√2, which is greater than v0.
Since the minimum speed of the charged particle cannot be v0 (it is actually v0√2), the assertion is false.
The reason states that a variable acceleration particle may be v0.
A charged particle moving in a magnetic field experiences a centripetal force that changes the direction of its velocity, leading to variable acceleration. The speed of the particle remains constant, but the direction changes, resulting in variable acceleration.
The statement that a variable acceleration particle may have a speed of v0 is true because the particle can indeed have a constant speed while experiencing variable acceleration due to the change in direction.
- The assertion is false.
- The reason is true.
- Assertion: False (minimum speed is v0√2).
- Reason: True (a charged particle can have constant speed while experiencing variable acceleration).
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
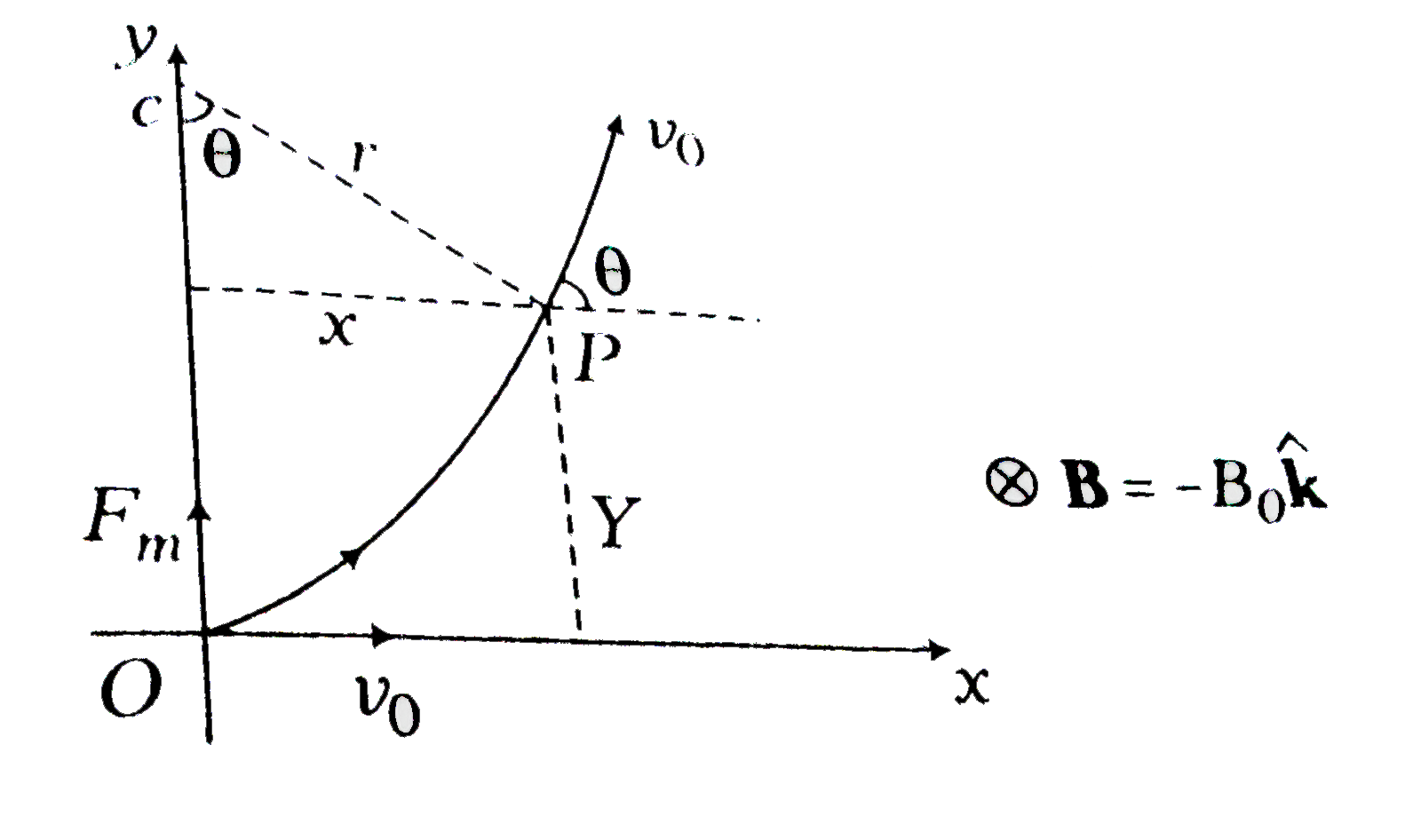
View Solution
Knowledge Check
A particle of mass m and charge q has and initial velocity →v=υ0ˆj. If an electric field →E=→–––(0)ˆi and magnetic field →B=B0ˆi act on the particle, its speed will double after a time :
At=2mv0qE0Bt=2B0qmv0Ct=√3B0qmv0Dt=√3mv0qE0
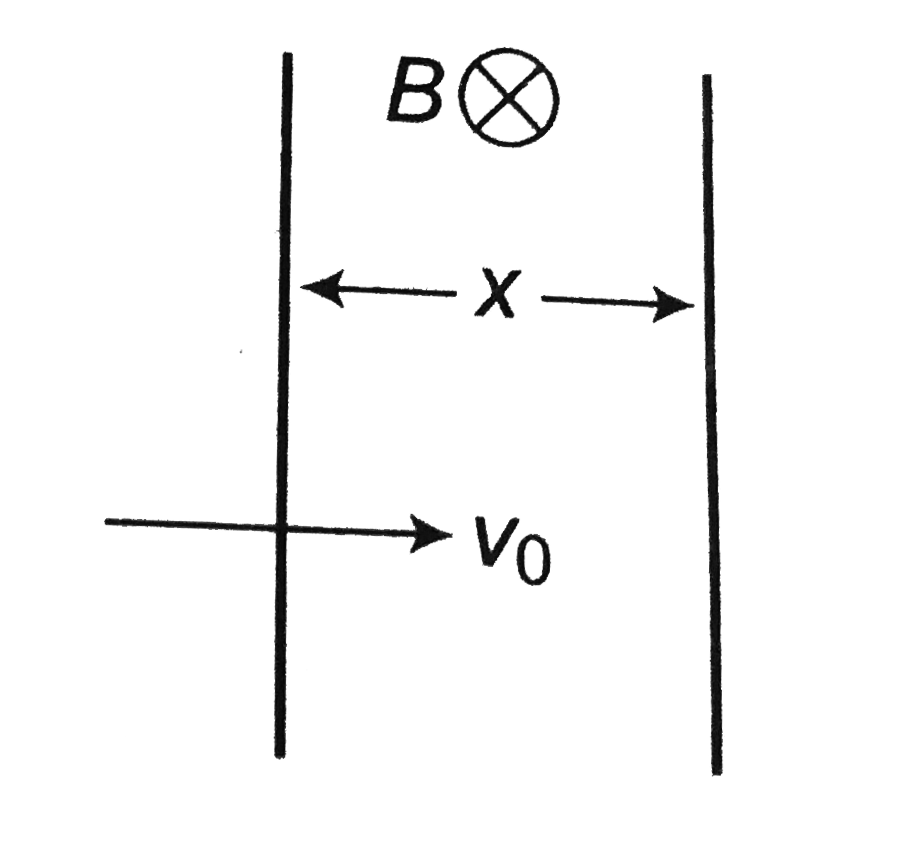
A charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
View SolutionWhen a charged particle moves in an elecltric or a magnetic field, its speed is v and acceleration is a
View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field →E=E0ˆiand→B=B0ˆi with a velocity →v=v0ˆj. The speed of the particle will become 2v0 after a time.
View SolutionA particle of mass m and charge q has and initial velocity →v=υ0ˆj. If an electric field →E=→–––(0)ˆi and magnetic field →B=B0ˆi act on the particle, its speed will double after a time :
View SolutionA charge q of mass m enters a region of electric field E=−E0ˆj with a velocity v0ˆi+v0ˆj at origin. Find the x coordinate where the charge hits the x axis again. (Neglect effect of gravity)
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View Solution
