A closed loop a current I lies in the xz-plane. The loop will experience a force if it is placed in a region occupied by uniform magnetic field along
x-axis
y-axis
z-axis
none of these
The correct Answer is:D
To solve the problem, we need to analyze the situation of a closed loop carrying a current I in the xz-plane when placed in a uniform magnetic field. Here is the step-by-step solution:
Step 1: Understand the Configuration
The closed loop lies in the xz-plane, meaning that the current flows in a plane defined by the x and z axes. We need to determine how this loop interacts with a uniform magnetic field.
Hint: Visualize the loop in the xz-plane and identify the direction of the current.
Step 2: Identify the Magnetic Field Direction
Let’s assume the uniform magnetic field is directed along the y-axis (B vector). This is a common scenario in such problems, but the direction can be specified differently.
Hint: Remember that the magnetic field can be oriented in any direction, but for simplicity, we often assume it is along one of the coordinate axes.
Step 3: Divide the Loop into Two Parts
To analyze the forces acting on the loop, we can divide the loop into two segments: the upper segment (above the x-axis) and the lower segment (below the x-axis).
Hint: Consider how the loop can be split into two parts for easier analysis of forces.
Step 4: Apply the Magnetic Force Formula
The magnetic force on a segment of the current-carrying loop can be calculated using the formula:
\( \vec{F} = I \vec{L} \times \vec{B} \)
where \( \vec{L} \) is the length vector of the segment and \( \vec{B} \) is the magnetic field vector.
Hint: Remember that the cross product will give a force that is perpendicular to both the current direction and the magnetic field direction.
Step 5: Calculate the Forces on Each Segment
For the upper segment of the loop, the force will be directed in one direction, and for the lower segment, the force will be directed in the opposite direction. Since the segments are equal in length and carry the same current, the magnitudes of the forces will be equal but opposite.
Hint: Use the right-hand rule to determine the direction of the force on each segment.
Step 6: Analyze the Net Force on the Loop
Since the forces on the upper and lower segments are equal in magnitude and opposite in direction, they will cancel each other out. Therefore, the net force on the closed loop will be zero.
Hint: Consider how the forces interact with each other and what the net effect is.
Conclusion
The closed loop carrying current I in the xz-plane will experience no net force when placed in a uniform magnetic field along the y-axis. Thus, the answer to the question is that the loop does not experience a force.
Final Answer: D) None of these.
The closed loop lies in the xz-plane, meaning that the current flows in a plane defined by the x and z axes. We need to determine how this loop interacts with a uniform magnetic field.
Let’s assume the uniform magnetic field is directed along the y-axis (B vector). This is a common scenario in such problems, but the direction can be specified differently.
To analyze the forces acting on the loop, we can divide the loop into two segments: the upper segment (above the x-axis) and the lower segment (below the x-axis).
The magnetic force on a segment of the current-carrying loop can be calculated using the formula:
\( \vec{F} = I \vec{L} \times \vec{B} \)
where \( \vec{L} \) is the length vector of the segment and \( \vec{B} \) is the magnetic field vector.
For the upper segment of the loop, the force will be directed in one direction, and for the lower segment, the force will be directed in the opposite direction. Since the segments are equal in length and carry the same current, the magnitudes of the forces will be equal but opposite.
Since the forces on the upper and lower segments are equal in magnitude and opposite in direction, they will cancel each other out. Therefore, the net force on the closed loop will be zero.
The closed loop carrying current I in the xz-plane will experience no net force when placed in a uniform magnetic field along the y-axis. Thus, the answer to the question is that the loop does not experience a force.
Topper's Solved these Questions
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:SCQ_TYPE
Explore 5 Videos
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:MCQ_TYPE
Explore 1 Video
- MAGNETICSBook:DC PANDEY ENGLISHChapter:MAGNETICSExercise:SUBJECTIVE_TYPE
Explore 1 Video
- MAGNETIC FIELD AND FORCESBook:DC PANDEY ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Medical entrance s gallery
Explore 59 Videos
- MAGNETISM AND MATTERBook:DC PANDEY ENGLISHChapter:MAGNETISM AND MATTERExercise:Medical gallery
Explore 1 Video
Similar Questions
Torque acting on a current loop in a uniform magnetic field is equal to
View SolutionA current loop in a magnetic field
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionWill a current loop placed in a magnetic field always experience a zero force?
View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

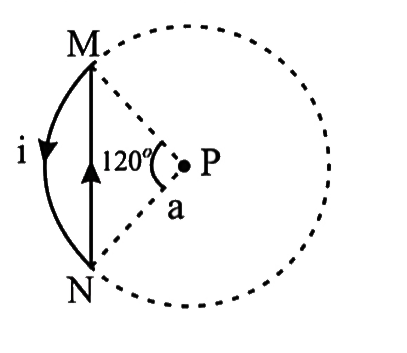
View Solutionconsider a triangular loop of wire with sides a and b. The loop carries a current I in the direction shown and is placed in a uniform magnetic field that has magnitude B and points in the same direction as the current in side OM of the loop. At the moment shown in the figure the torque on the current loop is τ. Find the value of IabB/τ
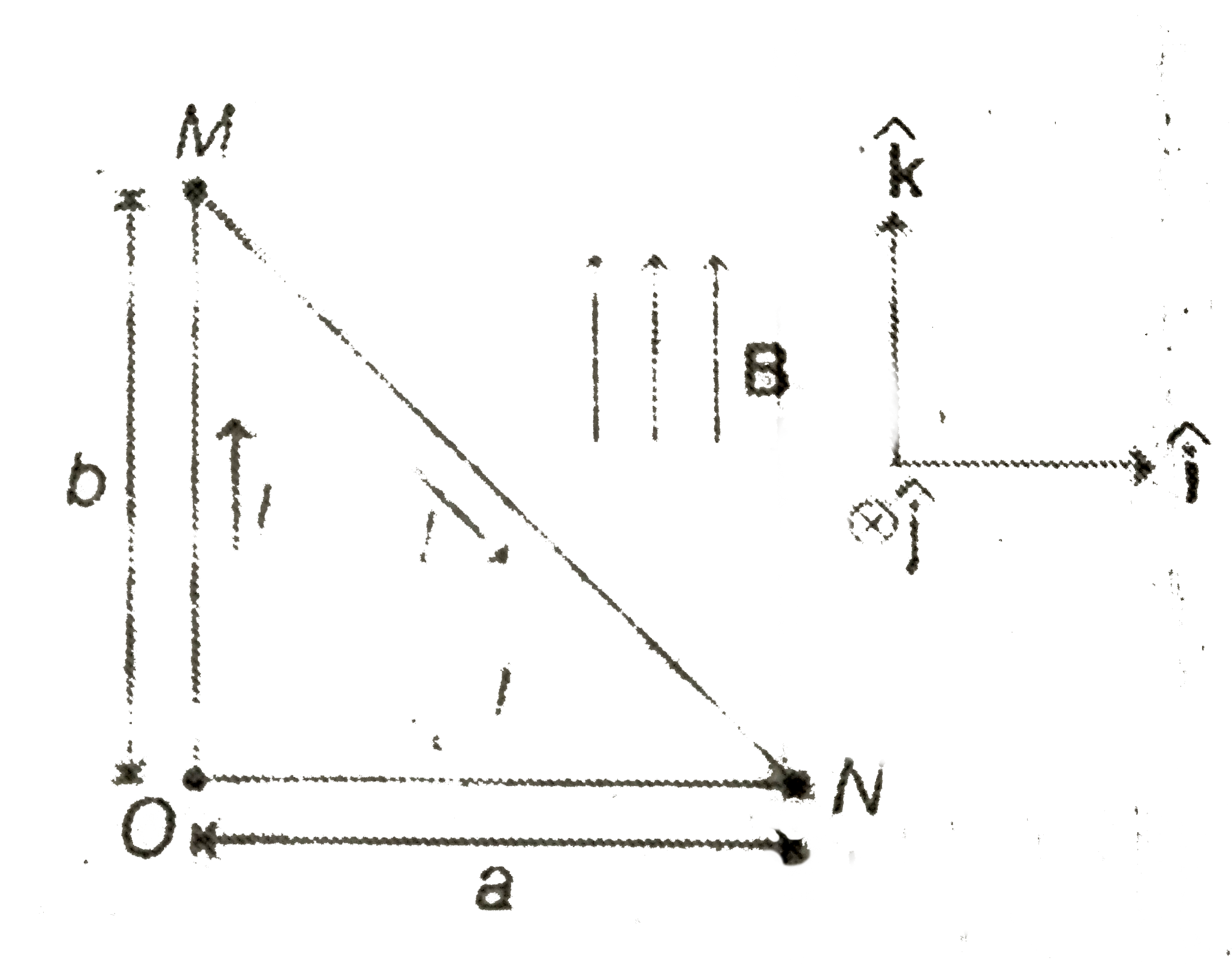
View Solution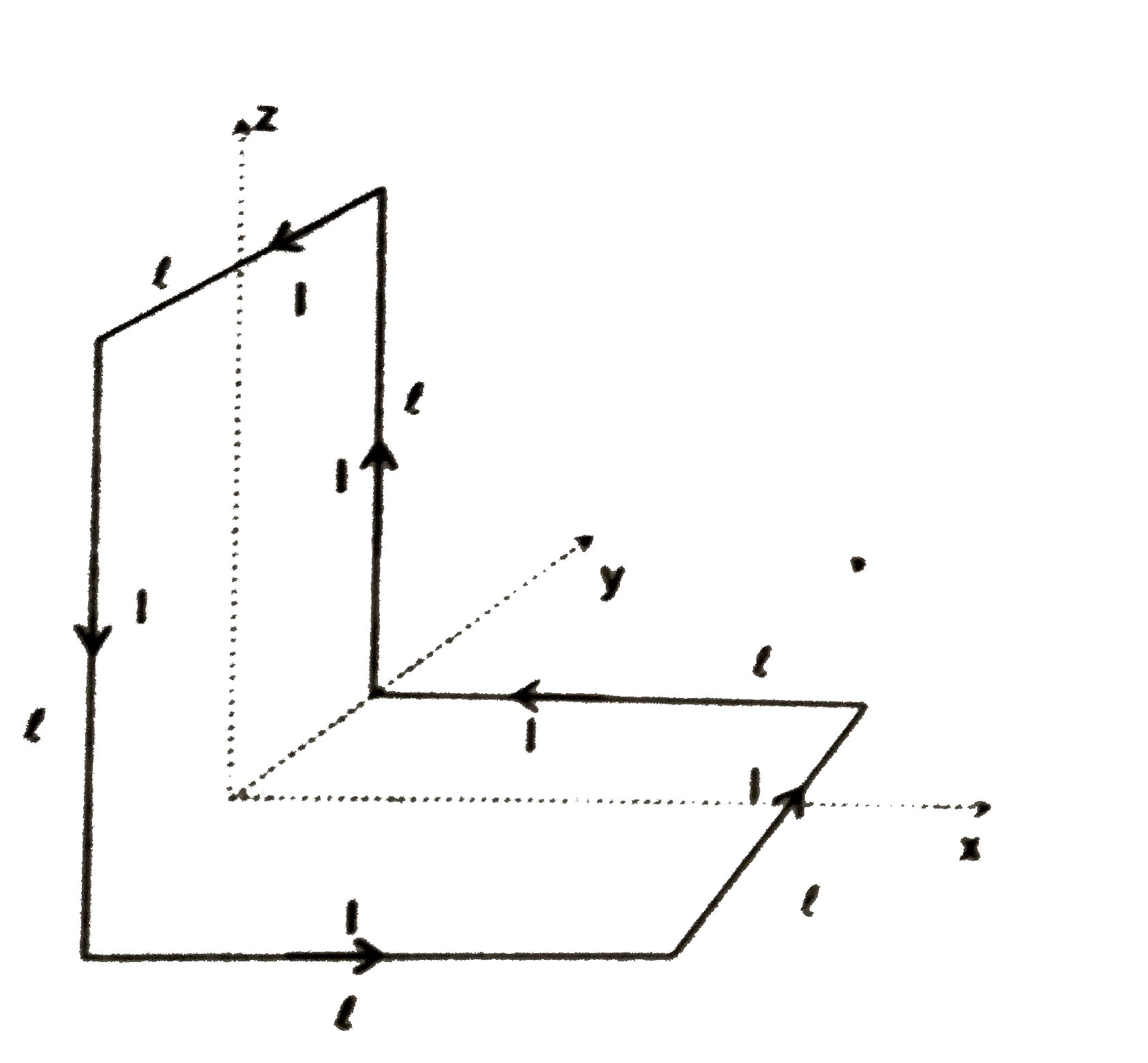
A conducting loop carrying current 'l' is bent into two halves and placed in mutually perpendicular planes xy and yz planes as shown. A uniform magnetic field →B=Bˆj is existing in the region. The net magnetic torque experienced by the loop is
View SolutionA current loop placed in a magnetic field behaves like a
View SolutionA circular loop carrying a current I is placed in the xy-plane as shown in figure. A uniform magnetic fied B is oriented along the positive z-axis. The loop tends to
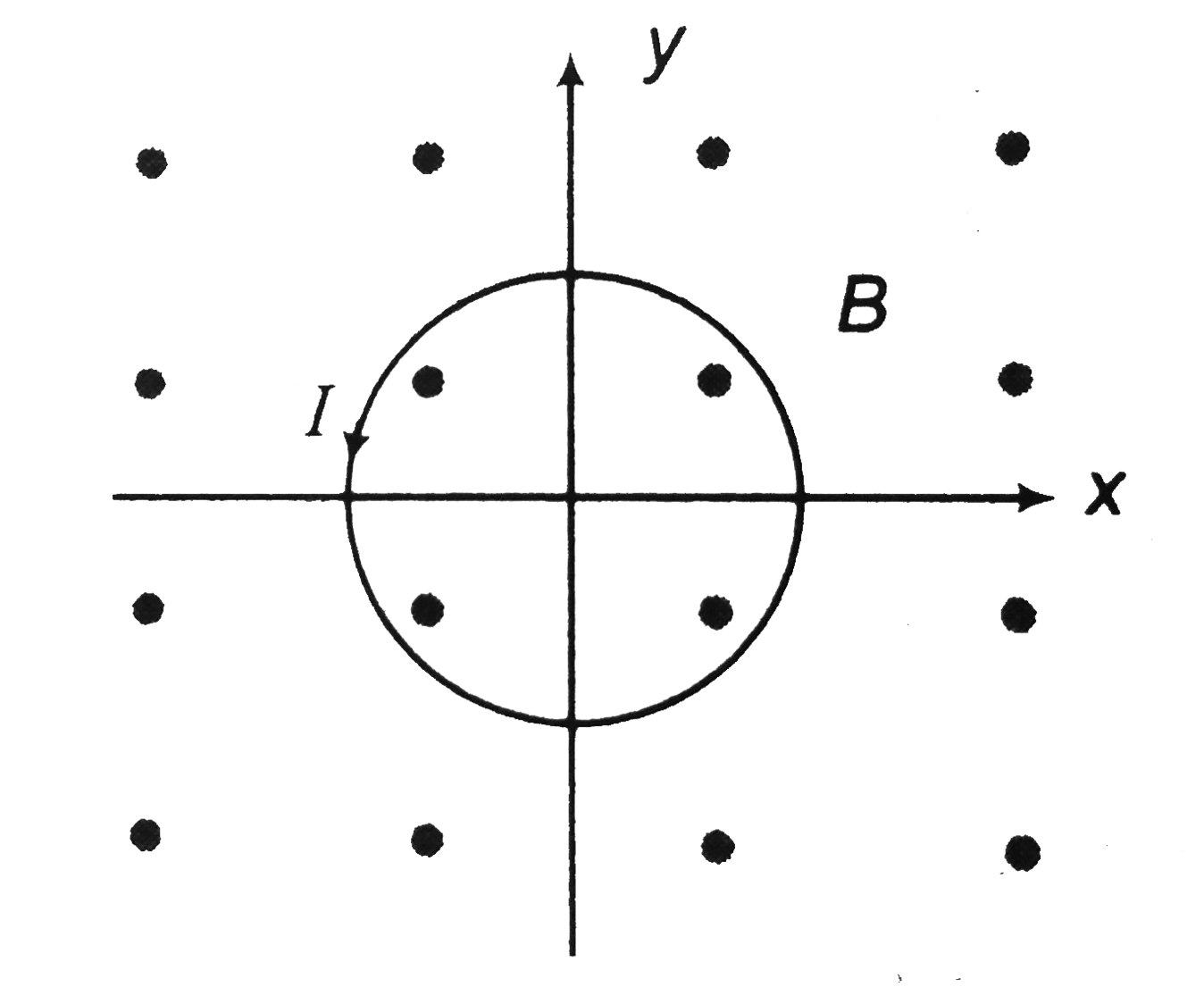
View Solution
