A conductor ab of arbitrary shape carries current I flowing from b to a. The length vector ab is oriented from a to b. The force F experienced by this conductor in as uniform magnetic field B is
F=−I(ab×B)
F=I(b×ab)
F=I(ba×B)
All of the above
The correct Answer is:D
To solve the problem of finding the force experienced by a conductor ab carrying current I in a uniform magnetic field B, we can follow these steps:
Step 1: Understand the Direction of Current and Length Vector
The current I is flowing from point B to point A, while the length vector (→L) is oriented from A to B. Therefore, we can express the length vector as:
\(
\vec{L} = \vec{AB} = \vec{b} - \vec{a}
\)
Step 2: Use the Formula for Magnetic Force
The force (→F) experienced by a current-carrying conductor in a magnetic field is given by the formula:
\(
\vec{F} = I \vec{L} \times \vec{B}
\)
Where:
- I is the current,
- (→L) is the length vector of the conductor,
- (→B) is the magnetic field.
Step 3: Substitute the Length Vector
Since the current is flowing from B to A, we can express the length vector as:
\(
\vec{L} = \vec{AB} = -(\vec{BA})
\)
Thus, we can rewrite the force as:
\(
\vec{F} = I (-\vec{BA}) \times \vec{B}
\)
This simplifies to:
\(
\vec{F} = -I \vec{BA} \times \vec{B}
\)
Step 4: Interpret the Cross Product
The cross product (−−→BA×→B) gives a vector that is perpendicular to both (−−→BA) and (→B). The negative sign indicates that the direction of the force is opposite to that of the vector (−−→BA×→B).
Step 5: Conclusion
The final expression for the force experienced by the conductor ab is:
\(
\vec{F} = -I \vec{BA} \times \vec{B}
\)
This indicates that the force is dependent on the current I, the length of the conductor, and the magnetic field B.
Summary of the Solution
The force experienced by the conductor ab in a uniform magnetic field B is given by:
\(
\vec{F} = I \vec{AB} \times \vec{B} = -I \vec{BA} \times \vec{B}
\)
---
The current I is flowing from point B to point A, while the length vector (→L) is oriented from A to B. Therefore, we can express the length vector as:
\(
\vec{L} = \vec{AB} = \vec{b} - \vec{a}
\)
The force (→F) experienced by a current-carrying conductor in a magnetic field is given by the formula:
\(
\vec{F} = I \vec{L} \times \vec{B}
\)
Where:
- I is the current,
- (→L) is the length vector of the conductor,
- (→B) is the magnetic field.
Since the current is flowing from B to A, we can express the length vector as:
\(
\vec{L} = \vec{AB} = -(\vec{BA})
\)
Thus, we can rewrite the force as:
\(
\vec{F} = I (-\vec{BA}) \times \vec{B}
\)
This simplifies to:
\(
\vec{F} = -I \vec{BA} \times \vec{B}
\)
The cross product (−−→BA×→B) gives a vector that is perpendicular to both (−−→BA) and (→B). The negative sign indicates that the direction of the force is opposite to that of the vector (−−→BA×→B).
The final expression for the force experienced by the conductor ab is:
\(
\vec{F} = -I \vec{BA} \times \vec{B}
\)
This indicates that the force is dependent on the current I, the length of the conductor, and the magnetic field B.
The force experienced by the conductor ab in a uniform magnetic field B is given by:
\(
\vec{F} = I \vec{AB} \times \vec{B} = -I \vec{BA} \times \vec{B}
\)
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
When is the force experienced by a current-carrying conductor placed in a magnetic field is largest?
View SolutionThe direction of force on a current carrying conductor in a magnetic field is given by
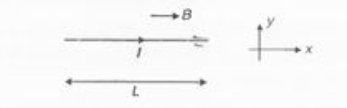
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
View SolutionA long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.
View SolutionA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
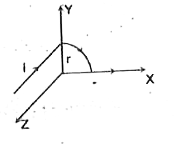
View SolutionShown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
View SolutionMention the angle between a current carrying conductor and magnetic field for which the force experienced by this current conductor placed field is largest ?
View SolutionA student while studying the force experienced by a current carrying conductor in a magnetic field records the following observations:
(i) The force experienced by the conductor increases as the current is increased.
(ii) The force experienced by the conductor decreases as the strength of the magnetic field is increased.
Which of the two observations is correct and why?
View SolutionThere long, straingth parallel wires carrying current, are arranged as shown in the figure. The force experienced by a 25 cm length of wire C is

View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View Solution
