A non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
is zero only for one orientation of loop in magnetic field
is zero for two symmetricaly located positions of loop in magnetic field
is zero for all orientations
is never zero
The correct Answer is:C
To solve the problem of finding the force acting on a non-planar closed loop of arbitrary shape carrying a current I placed in a uniform magnetic field B, we can follow these steps:
1. Understanding the Force on a Current-Carrying Wire:
The force F on a segment of wire carrying current I in a magnetic field B is given by the formula:
F=IL×B
where L is the length vector of the wire segment in the direction of the current.
2. Dividing the Loop into Segments:
Consider the closed loop as being composed of multiple segments. For simplicity, we can analyze two segments of the loop that are opposite each other. Let’s denote the upper segment as L1 and the lower segment as L2.
3. Analyzing the Forces on Each Segment:
- For the upper segment L1, the force acting on it due to the magnetic field is:
F1=IL1×B
- For the lower segment L2, the force acting on it is:
F2=IL2×B
Since L2 is in the opposite direction to L1, we can express L2 as −L1.
4. Calculating the Net Force:
Now, substituting L2=−L1 into the equation for F2:
F2=I(−L1)×B=−IL1×B
Thus, we have:
F1=IL1×B
F2=−IL1×B
5. Adding the Forces:
The net force Fnet acting on the loop is the sum of the forces on the segments:
Fnet=F1+F2=IL1×B−IL1×B=0
6. Conclusion:
Since the forces on opposite segments of the loop cancel each other out, the total force acting on the non-planar closed loop in a uniform magnetic field is:
Fnet=0
The force F on a segment of wire carrying current I in a magnetic field B is given by the formula:
F=IL×B
where L is the length vector of the wire segment in the direction of the current.
Consider the closed loop as being composed of multiple segments. For simplicity, we can analyze two segments of the loop that are opposite each other. Let’s denote the upper segment as L1 and the lower segment as L2.
- For the upper segment L1, the force acting on it due to the magnetic field is:
F1=IL1×B
- For the lower segment L2, the force acting on it is:
F2=IL2×B
Since L2 is in the opposite direction to L1, we can express L2 as −L1.
Now, substituting L2=−L1 into the equation for F2:
F2=I(−L1)×B=−IL1×B
Thus, we have:
F1=IL1×B
F2=−IL1×B
The net force Fnet acting on the loop is the sum of the forces on the segments:
Fnet=F1+F2=IL1×B−IL1×B=0
Since the forces on opposite segments of the loop cancel each other out, the total force acting on the non-planar closed loop in a uniform magnetic field is:
Fnet=0
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
Knowledge Check
A current carrying loop is placed in a uniform magnetic field. The torque acting on it does not depend upon
Aarea of loopBvalue of currentCmagnetic fieldDNone of these
A circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
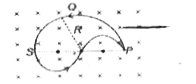
View SolutionA semicircular wire PQS of radius R is connected to a wire bent in the form of a sine curve to form a closed loop as shown in the figure. If the loop carries a current I and is placed in a uniform magnetic field B, then the total force acting on the sine curve is
View Solution(a) Write the expression for the force, →F, acting on a charged particle of charge 'q', moving with a velocity →V in the presence of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
(b) A rectangular loop of size l×b carrying a steady current I is placed in a uniform magnetic field →B. Prove that the torque →τ acting on the loop is given by
→τ=→m×→B, where →m is the magnetic moment of the loop.
View SolutionA current loop of arbitrary shape lies in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View SolutionA metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
View Solution
