A particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

Velocity of the particle at ay time t is
v(t)=vxˆi+vyˆj=v0cosθˆi+v0sinθˆj
or v(t)=v0cos(b0αt)ˆi+v0sin(B0αt)ˆj
Position of particle at t is
r(t)=xˆi+yˆj=rsinθˆi+(r−rcosθ)ˆj
substituting the values of r and θ we have
r(t)=v0B0α[sin(B0αt)ˆi+(1−cos(B0)αt))ˆj]
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
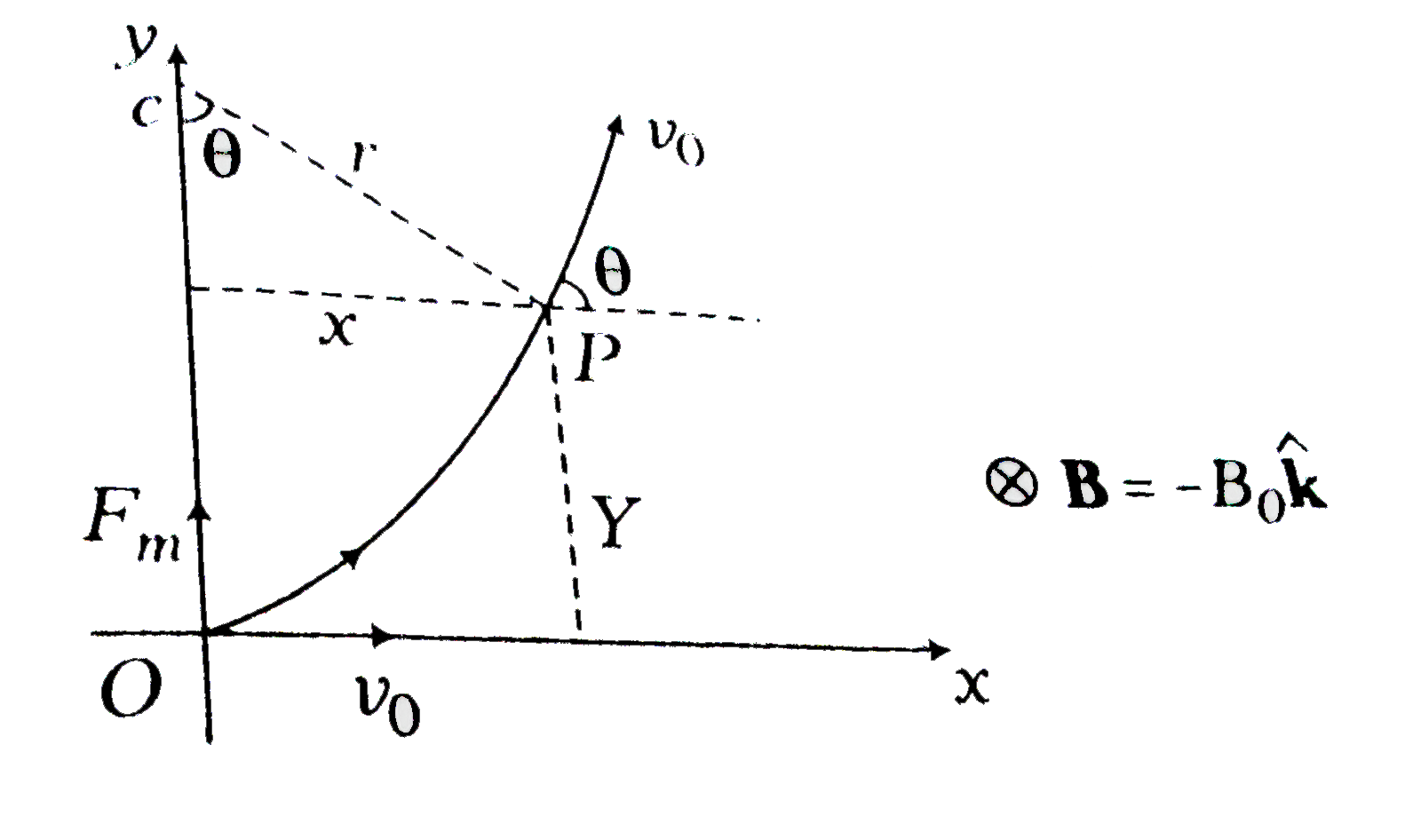
View SolutionA particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA proton and anα-particles enters in a uniform magnetic field with same velocity, then ratio of the radii of path describe by them
View SolutionA proton of charge e and mass m enters a uniform magnetic field B=Bi with an initial velocity v=vxˆi+vyˆj. Find an expression in unit vector notation for its velocity at time t.
View SolutionA charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionA proton of charge +e and mass m enters a uniform magnetic Field →B=ˆB with an intial velocity →v=v0xˆi+v0yˆj. Find an expression in unit-vector notation for its velocity at any later time t.
View SolutionA charge praticule of sepeific charge (charge/ mass ) α is realsed from origin at time t=0 with velocity v=v0(ˆi+ˆj) in unifrom magnetic fields B=B0ˆi. Co-ordinaties of the particle at time t=πB0α are
View SolutionAssertion: A charged particle enters in a magnetic field B=B0ˆiwithvelocityv=v0ˆi+v0ˆj, then minimum speed of charged particle may be v0.
Reason: A variable acceleration particle may be v0.
View SolutionA particle of mass m and charge +q enters a region of magnetic field with a velocity v, as shown in Fig. 1.93.
a. Find the angle subtended by the circular arc described by it in the magnetic field.
b. How long does the particle stay inside the magnetic field?
c. If the particle enters at E, what is the intercept EF?

View Solution
