A particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
To solve the problem, we need to analyze the motion of a charged particle in a magnetic field. The particle has a specific charge α and is projected from the origin with an initial velocity v=v0^i−v0^k in a uniform magnetic field B=−B0^k.
Step 1: Understanding the Motion
The magnetic field B is directed along the negative z-axis, while the initial velocity has components in the x and z directions. The y-component of the velocity is zero initially. The magnetic force will act on the particle, causing it to move in a circular path in the xy-plane, while the z-component of the velocity will remain unchanged.
Step 2: Magnetic Force Calculation
The magnetic force F acting on the particle is given by the Lorentz force equation:
F=q(v×B)
Substituting the values:
F=q((v0^i−v0^k)×(−B0^k))
Calculating the cross product:
(v0^i−v0^k)×(−B0^k)=v0B0^j
Thus, the magnetic force becomes:
F=qv0B0^j
Step 3: Centripetal Force and Angular Velocity
This magnetic force acts as the centripetal force required for circular motion:
F=mv2r
Setting the magnetic force equal to the centripetal force:
qv0B0=mv20r
From this, we can express the radius r:
r=mv0qB0
Using the specific charge α=qm, we can rewrite r:
r=v0αB0
Step 4: Angular Velocity
The angular velocity ω can be defined as:
ω=qB0m=αB0
Step 5: Time Dependence of Velocity
The angle θ rotated by the particle in the xy-plane at time t is given by:
θ=ωt=αB0t
Thus, the velocity components at any time t can be expressed as:
vx(t)=v0cos(θ)=v0cos(αB0t)
vy(t)=v0sin(θ)=v0sin(αB0t)
The z-component of the velocity remains unchanged:
vz(t)=−v0
Therefore, the velocity vector as a function of time is:
v(t)=v0cos(αB0t)^i+v0sin(αB0t)^j−v0^k
Step 6: Time Dependence of Position
The position components can be derived from the velocity:
x(t)=∫vx(t)dt=∫v0cos(αB0t)dt=v0αB0sin(αB0t)
y(t)=∫vy(t)dt=∫v0sin(αB0t)dt=−v0αB0cos(αB0t)+C
Since the particle starts at the origin, we can set C=v0αB0 to ensure y(0)=0:
y(t)=−v0αB0cos(αB0t)+v0αB0
The z-component remains unchanged:
z(t)=−v0t
Thus, the position vector as a function of time is:
r(t)=v0αB0sin(αB0t)^i+(−v0αB0cos(αB0t)+v0αB0)^j−v0t^k
Summary
The time dependence of the velocity and position of the particle is given by:
- Velocity:
v(t)=v0cos(αB0t)^i+v0sin(αB0t)^j−v0^k
- Position:
r(t)=v0αB0sin(αB0t)^i+(−v0αB0cos(αB0t)+v0αB0)^j−v0t^k
The magnetic field B is directed along the negative z-axis, while the initial velocity has components in the x and z directions. The y-component of the velocity is zero initially. The magnetic force will act on the particle, causing it to move in a circular path in the xy-plane, while the z-component of the velocity will remain unchanged.
The magnetic force F acting on the particle is given by the Lorentz force equation:
F=q(v×B)
Substituting the values:
F=q((v0^i−v0^k)×(−B0^k))
Calculating the cross product:
(v0^i−v0^k)×(−B0^k)=v0B0^j
Thus, the magnetic force becomes:
F=qv0B0^j
This magnetic force acts as the centripetal force required for circular motion:
F=mv2r
Setting the magnetic force equal to the centripetal force:
qv0B0=mv20r
From this, we can express the radius r:
r=mv0qB0
Using the specific charge α=qm, we can rewrite r:
r=v0αB0
The angular velocity ω can be defined as:
ω=qB0m=αB0
The angle θ rotated by the particle in the xy-plane at time t is given by:
θ=ωt=αB0t
Thus, the velocity components at any time t can be expressed as:
vx(t)=v0cos(θ)=v0cos(αB0t)
vy(t)=v0sin(θ)=v0sin(αB0t)
The z-component of the velocity remains unchanged:
vz(t)=−v0
Therefore, the velocity vector as a function of time is:
v(t)=v0cos(αB0t)^i+v0sin(αB0t)^j−v0^k
The position components can be derived from the velocity:
x(t)=∫vx(t)dt=∫v0cos(αB0t)dt=v0αB0sin(αB0t)
y(t)=∫vy(t)dt=∫v0sin(αB0t)dt=−v0αB0cos(αB0t)+C
Since the particle starts at the origin, we can set C=v0αB0 to ensure y(0)=0:
y(t)=−v0αB0cos(αB0t)+v0αB0
The z-component remains unchanged:
z(t)=−v0t
Thus, the position vector as a function of time is:
r(t)=v0αB0sin(αB0t)^i+(−v0αB0cos(αB0t)+v0αB0)^j−v0t^k
The time dependence of the velocity and position of the particle is given by:
- Velocity:
v(t)=v0cos(αB0t)^i+v0sin(αB0t)^j−v0^k
- Position:
r(t)=v0αB0sin(αB0t)^i+(−v0αB0cos(αB0t)+v0αB0)^j−v0t^k
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View SolutionA charge praticule of sepeific charge (charge/ mass ) α is realsed from origin at time t=0 with velocity v=v0(ˆi+ˆj) in unifrom magnetic fields B=B0ˆi. Co-ordinaties of the particle at time t=πB0α are
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.
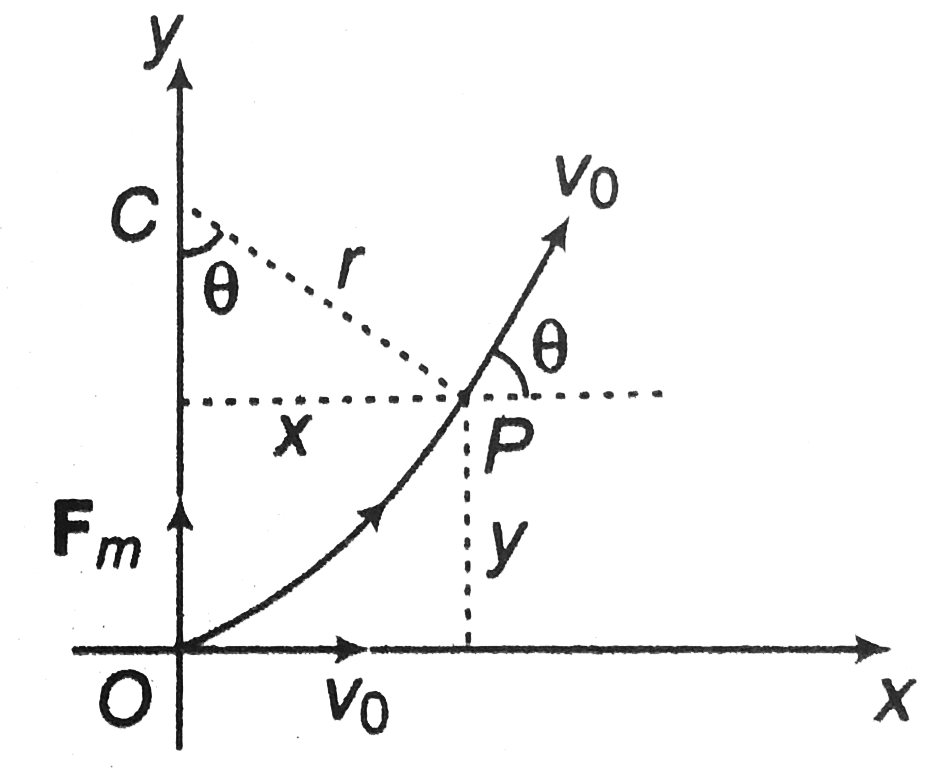
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
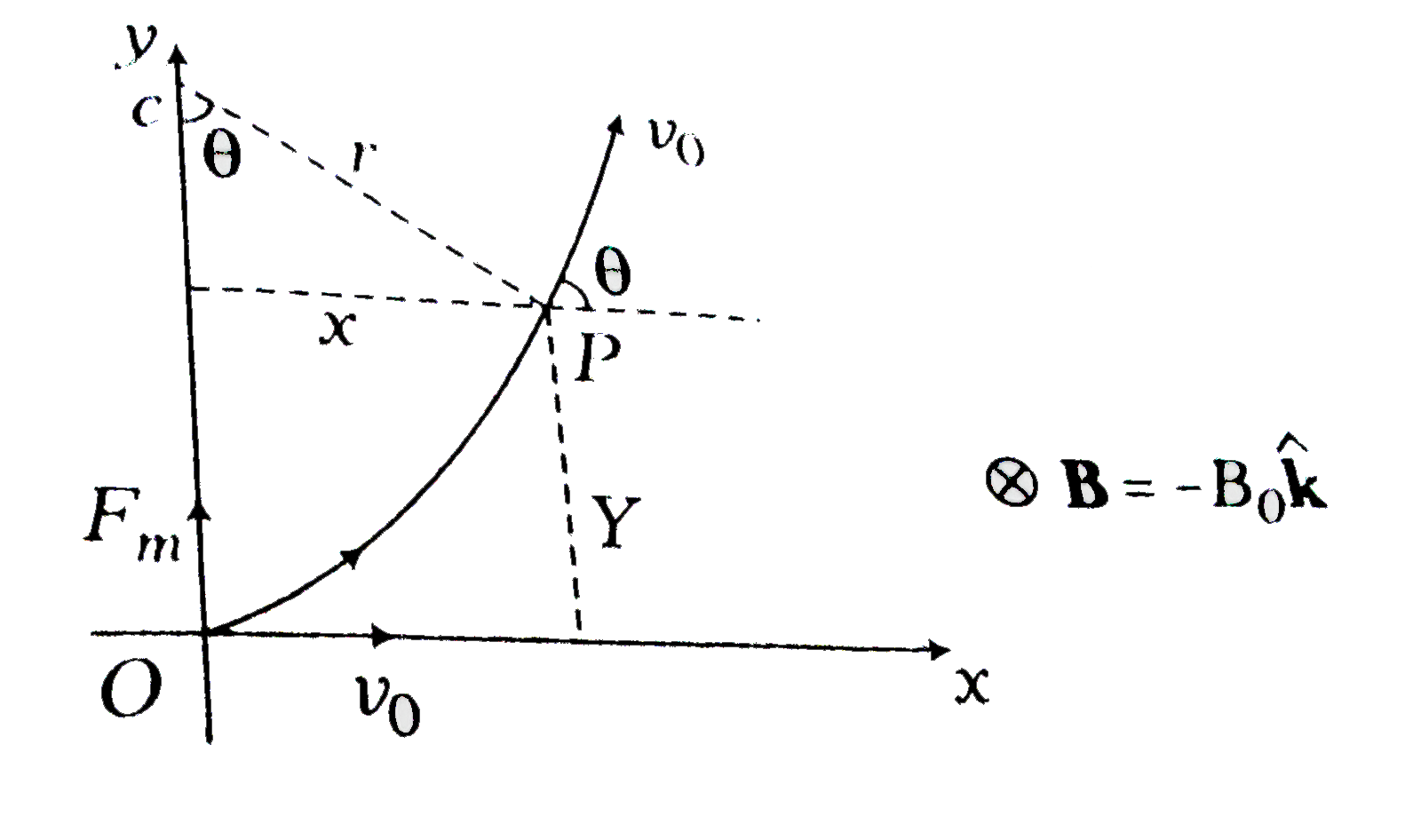
View SolutionIn uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Pitch of helical path described by particle is
View SolutionIn uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Angle between v and B is
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi uniform magnetic field →B=−B0ˆk. If the particle passes through (0,y,0), then y is equal to
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Pitch of the helical path described by the particle is
View SolutionA charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Maximum z-coordinate of the particle is
View Solution
