Assertion : When an uncharged capacitor is charged by a battery only 50% of the energy supplied is stored in the capacitor.
Reason : Rest 50% is lost.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:A, B
To solve the question, we need to analyze the assertion and the reason provided regarding the energy stored in a capacitor when charged by a battery.
1. Understanding the Assertion:
The assertion states that when an uncharged capacitor is charged by a battery, only 50% of the energy supplied is stored in the capacitor.
2. Understanding the Reason:
The reason provided states that the rest 50% of the energy is lost.
3. Energy Supplied by the Battery:
When a capacitor of capacitance C is charged by a battery of voltage V, the total charge Q on the capacitor is given by:
Q=CV
The work done (or energy supplied) by the battery to charge the capacitor is:
W=Q⋅V=CV⋅V=CV2
4. Energy Stored in the Capacitor:
The potential energy U stored in a capacitor is given by the formula:
U=12CV2
5. Calculating the Energy Loss:
To find the energy lost, we can compare the energy supplied by the battery to the energy stored in the capacitor:
- Energy supplied by the battery: CV2
- Energy stored in the capacitor: 12CV2
The energy lost can be calculated as:
Energy lost=Energy supplied−Energy stored=CV2−12CV2=12CV2
6. Conclusion:
From the above calculations, we see that indeed only 50% of the energy supplied by the battery is stored in the capacitor, while the other 50% is lost (usually as heat due to resistance in the circuit). Therefore, both the assertion and the reason are true, and the reason correctly explains the assertion.
Final Answer:
- Both the assertion and reason are true, and the reason is the correct explanation for the assertion.
---
The assertion states that when an uncharged capacitor is charged by a battery, only 50% of the energy supplied is stored in the capacitor.
The reason provided states that the rest 50% of the energy is lost.
When a capacitor of capacitance C is charged by a battery of voltage V, the total charge Q on the capacitor is given by:
Q=CV
The work done (or energy supplied) by the battery to charge the capacitor is:
W=Q⋅V=CV⋅V=CV2
The potential energy U stored in a capacitor is given by the formula:
U=12CV2
To find the energy lost, we can compare the energy supplied by the battery to the energy stored in the capacitor:
- Energy supplied by the battery: CV2
- Energy stored in the capacitor: 12CV2
Energy lost=Energy supplied−Energy stored=CV2−12CV2=12CV2
From the above calculations, we see that indeed only 50% of the energy supplied by the battery is stored in the capacitor, while the other 50% is lost (usually as heat due to resistance in the circuit). Therefore, both the assertion and the reason are true, and the reason correctly explains the assertion.
- Both the assertion and reason are true, and the reason is the correct explanation for the assertion.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Assertion : When a capacitor is charged by a battery. Half of the energy supplied by the battery is stored in the capacitor and rest half is lost.
Reason : If resistance in the circuit is zero, then there will be no loss of energy.
View SolutionAn uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is
View Solution
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4J
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionAn uncharged capacitor is connected to a battery. Show that half the energy supplied by the battery is lost as heat while charging the capacitor.
View SolutionProve that in charging a capacitor half of the energy supplied by the battery is stored in the capacitor and remaining half is lost during charging.
View SolutionThree initially uncharged capacitors are arranged with batteries as shown in. Find the charge on each capacitor.
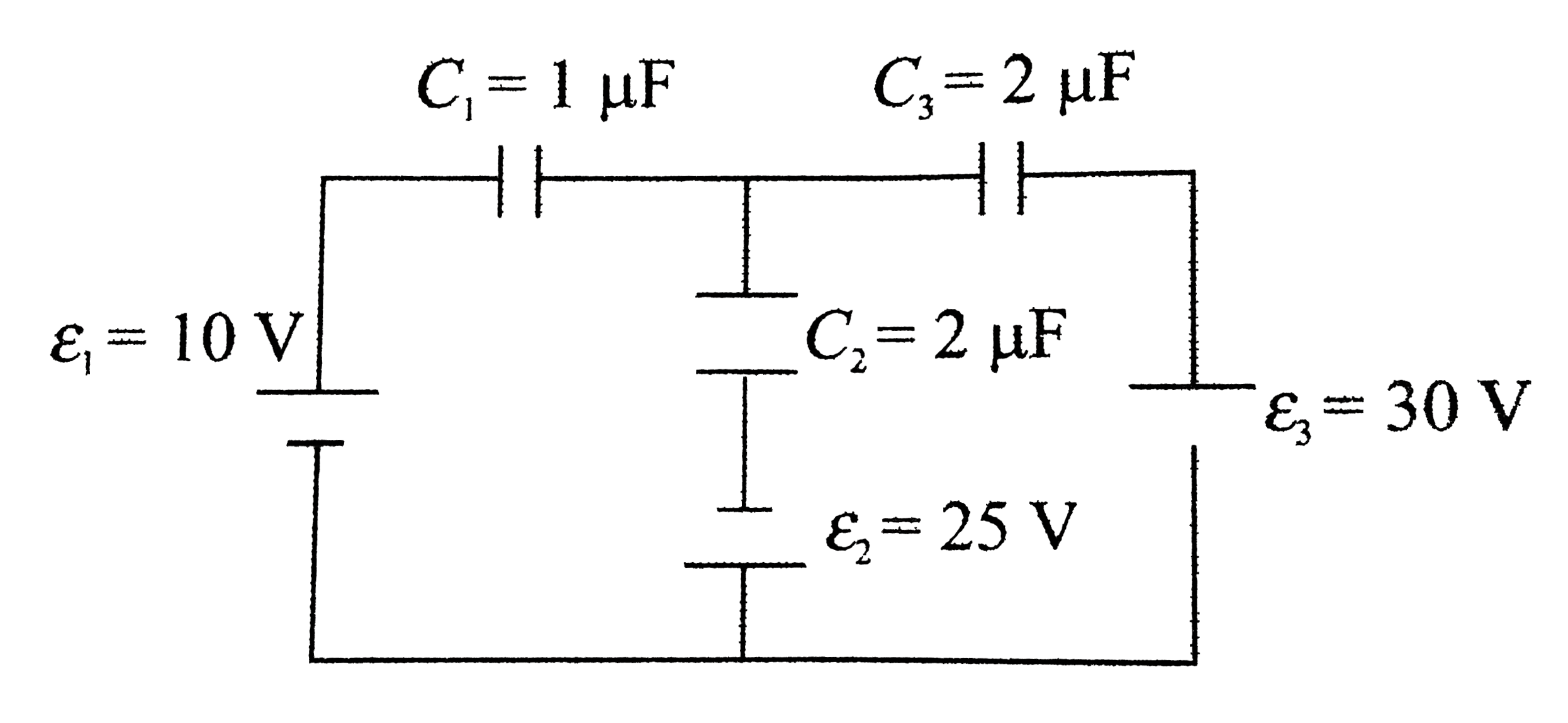 .
.
View SolutionBy evaluating ∫i2Rdt,show that when a capacitor is charged by connecting it to a battery through a resistor,the energy dissipated as heat equals the energy stored in the capacitor.
View SolutionThree uncharged capacitors are connected across a battery as shown. It is known that the energy stored in all the capacitors is same. Which of the following is not correct?

View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
View Solution
