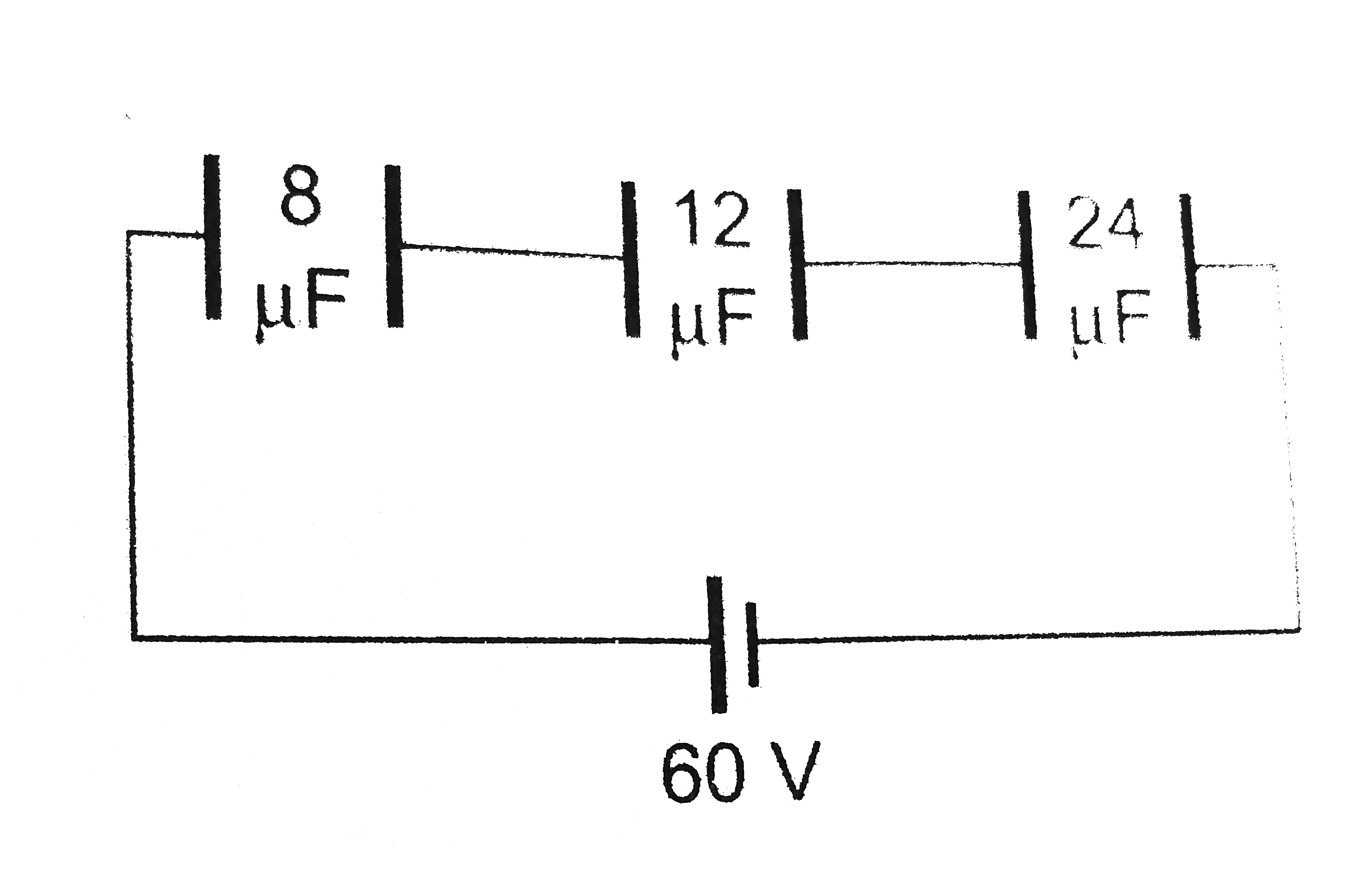
n identical capacitors are connected in parallel to a potential difference V. These capacitors are then reconnected in series, their charges being left undisturbed. The potential difference obtained is
zero
(n−1)V
nV
n2V
The correct Answer is:C
To solve the problem step by step, we will analyze the situation of n identical capacitors connected first in parallel and then in series.
Step 1: Understanding Capacitors in Parallel
When n identical capacitors are connected in parallel to a potential difference V, each capacitor experiences the same voltage V. The charge Q on each capacitor can be expressed as:
\(
Q = C \cdot V
\)
where \( C \) is the capacitance of each capacitor.
Step 2: Total Charge in Parallel
Since there are n identical capacitors connected in parallel, the total charge \( Q_{total} \) stored in the system is the sum of the charges on each capacitor:
\(
Q_{total} = n \cdot Q = n \cdot (C \cdot V) = nCV
\)
Step 3: Reconnecting Capacitors in Series
Next, we reconnect these n capacitors in series. In a series connection, the charge \( Q \) on each capacitor remains the same, and the total potential difference \( V_{total} \) across the series combination is the sum of the potential differences across each capacitor.
Step 4: Potential Difference Across Each Capacitor in Series
The potential difference across each capacitor when connected in series is given by:
\(
V_i = \frac{Q}{C}
\)
Since the charge \( Q \) remains the same for each capacitor, we can substitute \( Q \) with \( nCV \) (from Step 2):
\(
V_i = \frac{nCV}{C} = nV
\)
Step 5: Total Potential Difference in Series
The total potential difference \( V_{total} \) across the series connection of n capacitors is:
\(
V_{total} = V_1 + V_2 + ... + V_n = nV
\)
Conclusion
Thus, when n identical capacitors are connected in parallel to a potential difference V and then reconnected in series, the total potential difference obtained is:
\(
\boxed{nV}
\)
---
When n identical capacitors are connected in parallel to a potential difference V, each capacitor experiences the same voltage V. The charge Q on each capacitor can be expressed as:
\(
Q = C \cdot V
\)
where \( C \) is the capacitance of each capacitor.
Since there are n identical capacitors connected in parallel, the total charge \( Q_{total} \) stored in the system is the sum of the charges on each capacitor:
\(
Q_{total} = n \cdot Q = n \cdot (C \cdot V) = nCV
\)
Next, we reconnect these n capacitors in series. In a series connection, the charge \( Q \) on each capacitor remains the same, and the total potential difference \( V_{total} \) across the series combination is the sum of the potential differences across each capacitor.
The potential difference across each capacitor when connected in series is given by:
\(
V_i = \frac{Q}{C}
\)
Since the charge \( Q \) remains the same for each capacitor, we can substitute \( Q \) with \( nCV \) (from Step 2):
\(
V_i = \frac{nCV}{C} = nV
\)
The total potential difference \( V_{total} \) across the series connection of n capacitors is:
\(
V_{total} = V_1 + V_2 + ... + V_n = nV
\)
Thus, when n identical capacitors are connected in parallel to a potential difference V and then reconnected in series, the total potential difference obtained is:
\(
\boxed{nV}
\)
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Knowledge Check
Two idential capacitors are joined in parallel, charged to a potential V and then separated and then connected in series i.e. the positive plate of one is connected to negative of the other
AThe charges on the free plated connected together are destoyed.BThe energy stored in the system increases.CThe potential difference between the free plates is 2V.DThe potential difference remains constant.
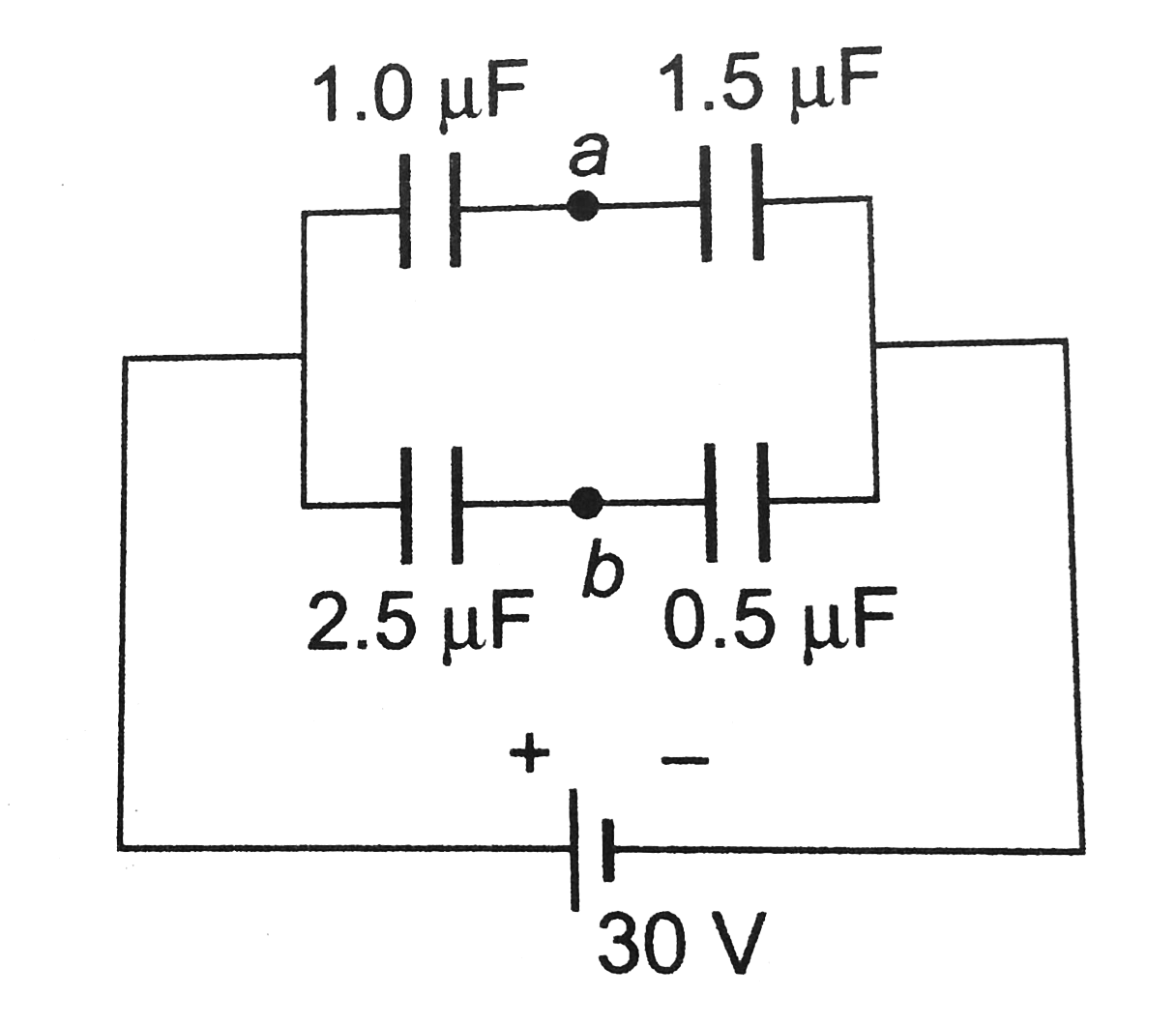
Four capacitors are connected as shown in figuere to a 30V battery. The potential difference between points a and b
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionA capacitor of capacitance C is charged to a potential difference V from a cell and then disconncted from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
View SolutionTwo identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is
View SolutionAn air capacitor is charged upto a potential V1. It is connected in parallel to an identical uncharged capacitor filled with a dielectric medium. After redistribution of charge if the potential difference of this combination is V, then the dielectric constant of the substance will be
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View Solution