Prove that in charging a capacitor half of the energy supplied by the battery is stored in the capacitor and remaining half is lost during charging.
To prove that in charging a capacitor, half of the energy supplied by the battery is stored in the capacitor and the remaining half is lost during charging, we can follow these steps:
Step 1: Determine the Energy Supplied by the Battery
When a capacitor of capacitance C is connected to a battery with voltage V, the total charge Q on the capacitor is given by:
Q=CV
The energy supplied by the battery (UB) when charging the capacitor can be calculated as:
UB=Q⋅V
Substituting Q from the first equation:
UB=(CV)⋅V=CV2
This is our Equation 1.
Step 2: Calculate the Energy Stored in the Capacitor
The energy stored in the capacitor (UC) can be derived using the concept of integration. The energy stored in a capacitor is given by:
UC=∫Q0VdQ
Since V across the capacitor varies as it charges, we can express V in terms of Q:
V=QC
Thus, the energy stored becomes:
UC=∫Q0QCdQ
Calculating this integral:
UC=1C∫Q0QdQ=1C(Q22)Q0=Q22C
Substituting Q=CV:
UC=(CV)22C=12CV2
This is our Equation 2.
Step 3: Compare the Energy Supplied and Stored
From Equations 1 and 2, we have:
- Energy supplied by the battery: UB=CV2
- Energy stored in the capacitor: UC=12CV2
Step 4: Calculate the Energy Lost
The energy lost during the charging process can be calculated as:
Energy lost=UB−UC=CV2−12CV2=12CV2
Conclusion
Thus, we have shown that:
- Half of the energy supplied by the battery is stored in the capacitor: UC=12UB
- The remaining half is lost during charging: Energy lost=12UB
Therefore, it is proved that during the charging of a capacitor, half of the energy supplied by the battery is stored in the capacitor and the remaining half is lost.
When a capacitor of capacitance C is connected to a battery with voltage V, the total charge Q on the capacitor is given by:
Q=CV
The energy supplied by the battery (UB) when charging the capacitor can be calculated as:
UB=Q⋅V
Substituting Q from the first equation:
UB=(CV)⋅V=CV2
This is our Equation 1.
The energy stored in the capacitor (UC) can be derived using the concept of integration. The energy stored in a capacitor is given by:
UC=∫Q0VdQ
Since V across the capacitor varies as it charges, we can express V in terms of Q:
V=QC
Thus, the energy stored becomes:
UC=∫Q0QCdQ
Calculating this integral:
UC=1C∫Q0QdQ=1C(Q22)Q0=Q22C
Substituting Q=CV:
UC=(CV)22C=12CV2
This is our Equation 2.
From Equations 1 and 2, we have:
- Energy supplied by the battery: UB=CV2
- Energy stored in the capacitor: UC=12CV2
The energy lost during the charging process can be calculated as:
Energy lost=UB−UC=CV2−12CV2=12CV2
Thus, we have shown that:
- Half of the energy supplied by the battery is stored in the capacitor: UC=12UB
- The remaining half is lost during charging: Energy lost=12UB
Topper's Solved these Questions
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:Exercise
Explore 155 Videos
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- ATOMSBook:DC PANDEY ENGLISHChapter:ATOMSExercise:MEDICAL ENTRANCES GALLERY
Explore 42 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
Similar Questions
Find the charge stored in the capacitor.
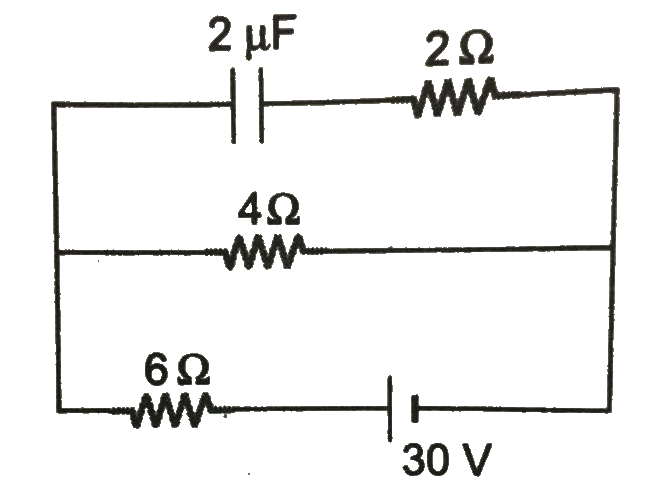
View SolutionFind the charge stored in the capacitor.
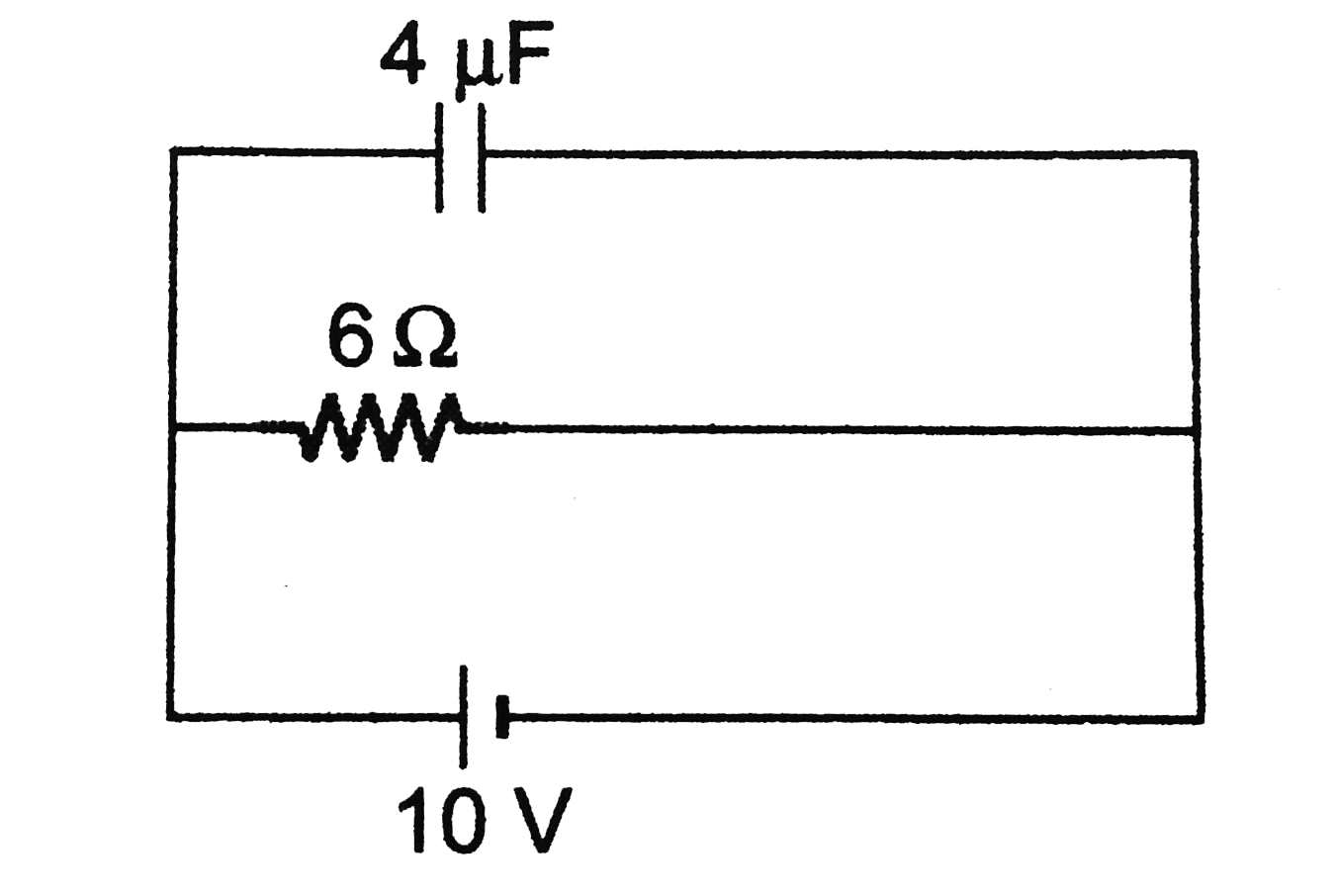
View SolutionFind the charge stored in the capacitor.
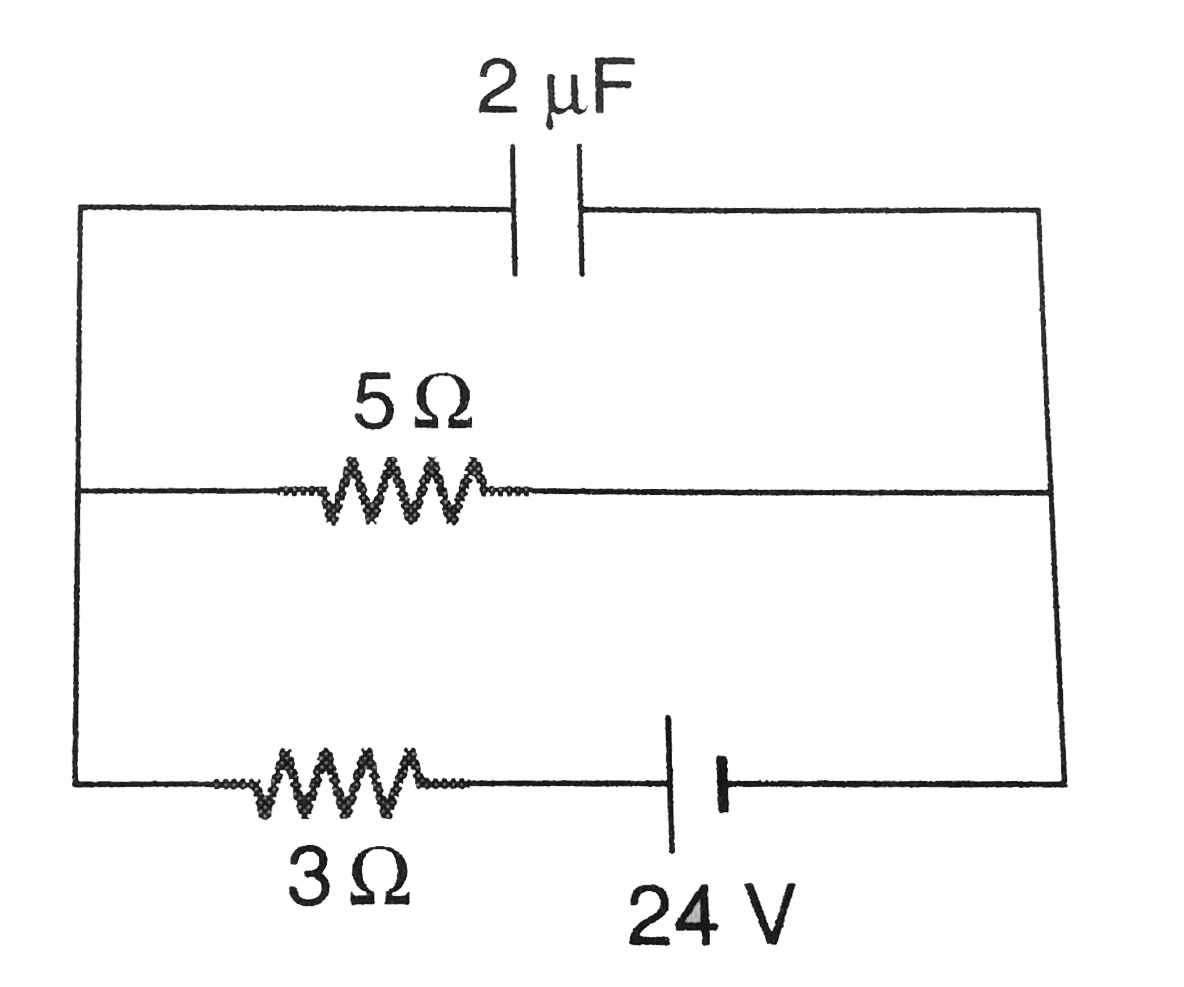
View SolutionAssertion : When a capacitor is charged by a battery. Half of the energy supplied by the battery is stored in the capacitor and rest half is lost.
Reason : If resistance in the circuit is zero, then there will be no loss of energy.
View SolutionFind the charged stored in all the capacitors
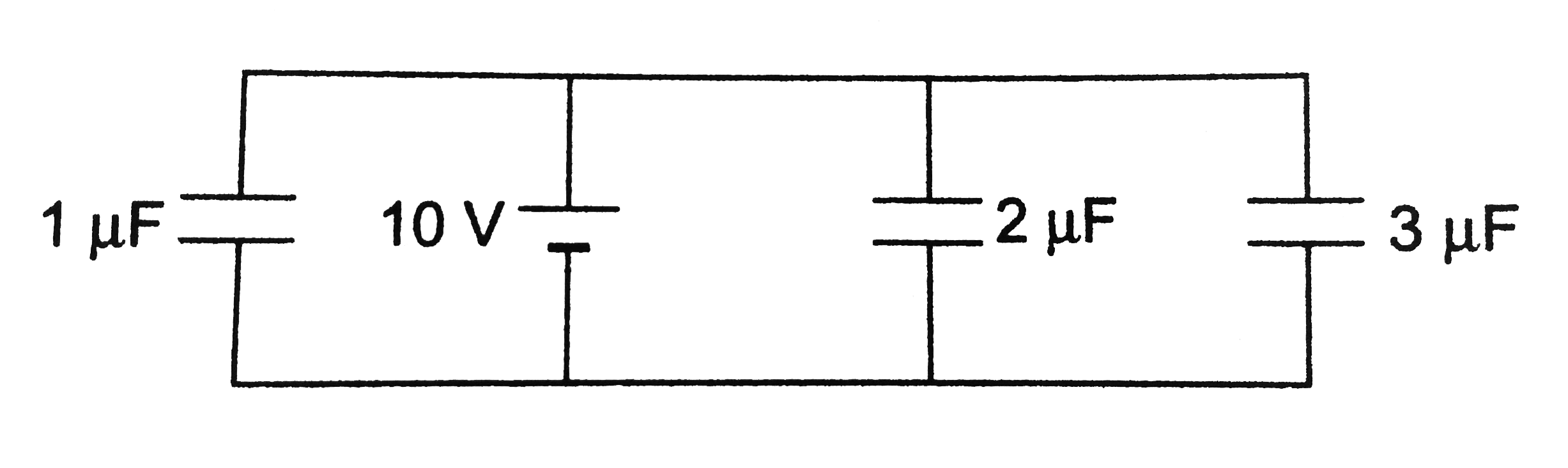
View SolutionIn a charged capacitor, the energy resides in
View SolutionAssertion : When an uncharged capacitor is charged by a battery only 50% of the energy supplied is stored in the capacitor.
Reason : Rest 50% is lost.
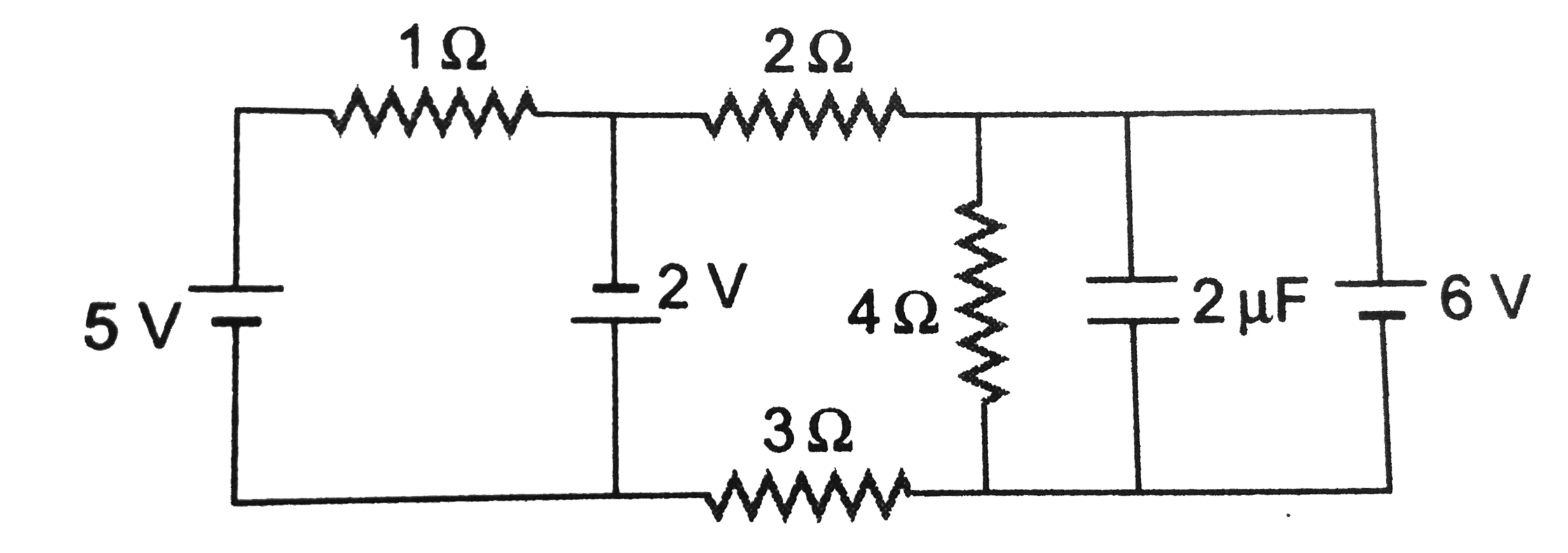
View SolutionThe current in 1Ω resistance and charge stored in the capacitor are
View SolutionA battery does 200 J of work in charging a capacitor. The energy stored is.
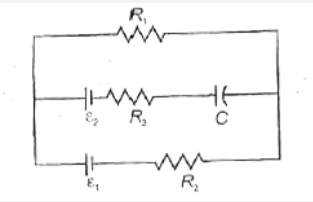
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
View Solution

