By evaluating ∫i2Rdt,show that when a capacitor is charged by connecting it to a battery through a resistor,the energy dissipated as heat equals the energy stored in the capacitor.
To show that the energy dissipated as heat equals the energy stored in the capacitor when it is charged through a resistor, we will evaluate the integral ∫I2Rdt.
1. Understanding the Circuit:
- We have a capacitor being charged through a resistor R from a battery. The current I in the circuit can be expressed as:
I(t)=I0e−tRC
where I0 is the initial current at t=0.
2. Expression for Heat Dissipated:
- The heat H dissipated in the resistor can be calculated using the formula:
H=∫I2Rdt
- Substituting the expression for I(t):
H=∫(I0e−tRC)2Rdt=∫I20e−2tRCRdt
3. Taking Constants Outside the Integral:
- Since I20 and R are constants, we can factor them out:
H=I20R∫e−2tRCdt
4. Evaluating the Integral:
- The integral ∫e−2tRCdt can be computed:
∫e−2tRCdt=−RC2e−2tRC+C
- Therefore, substituting back:
H=I20R(−RC2e−2tRC)+C
- This simplifies to:
H=−I20R2C2e−2tRC
5. Energy Stored in the Capacitor:
- The energy U stored in the capacitor when it is fully charged is given by:
U=12CV2
- From Ohm's law, V=IR and substituting I=I0e−tRC:
V2=(I0e−tRCR)2=I20R2e−2tRC
- Thus, the energy stored becomes:
U=12C(I20R2e−2tRC)
6. Equating Heat and Stored Energy:
- From the expressions derived, we see that:
H=−I20R2C2e−2tRC=U
- Therefore, the energy dissipated as heat equals the energy stored in the capacitor.
Conclusion:
We have shown that when a capacitor is charged through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
---
- We have a capacitor being charged through a resistor R from a battery. The current I in the circuit can be expressed as:
I(t)=I0e−tRC
where I0 is the initial current at t=0.
- The heat H dissipated in the resistor can be calculated using the formula:
H=∫I2Rdt
- Substituting the expression for I(t):
H=∫(I0e−tRC)2Rdt=∫I20e−2tRCRdt
- Since I20 and R are constants, we can factor them out:
H=I20R∫e−2tRCdt
- The integral ∫e−2tRCdt can be computed:
∫e−2tRCdt=−RC2e−2tRC+C
- Therefore, substituting back:
H=I20R(−RC2e−2tRC)+C
- This simplifies to:
H=−I20R2C2e−2tRC
- The energy U stored in the capacitor when it is fully charged is given by:
U=12CV2
- From Ohm's law, V=IR and substituting I=I0e−tRC:
V2=(I0e−tRCR)2=I20R2e−2tRC
- Thus, the energy stored becomes:
U=12C(I20R2e−2tRC)
- From the expressions derived, we see that:
H=−I20R2C2e−2tRC=U
- Therefore, the energy dissipated as heat equals the energy stored in the capacitor.
We have shown that when a capacitor is charged through a resistor, the energy dissipated as heat equals the energy stored in the capacitor.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer
17 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
An uncharged capacitor is connected to a battery. Show that half the energy supplied by the battery is lost as heat while charging the capacitor.
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionA 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionAn Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionThe switch shown in figure is suddenly closed. Find the current through the resistor when energy dissipated in the resistor is one third of total energy dissipated in the resistor.

View SolutionFind the total energy stored in the capacitors in the given network.
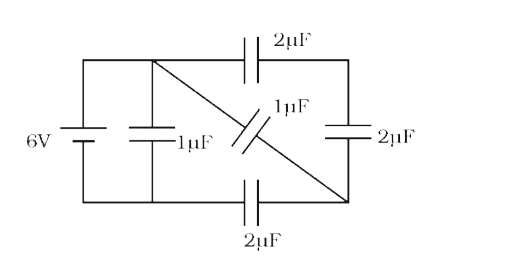
View SolutionAssertion : When an uncharged capacitor is charged by a battery only 50% of the energy supplied is stored in the capacitor.
Reason : Rest 50% is lost.
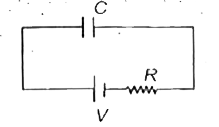
View SolutionAs in the figure, if a capacitor of capacitance 'C' is charged by connecting it with resistance R, then energy given by the battery will be
View SolutionIf there are n capacitors in parallel connected to V volt source, then the energy stored is equal to
View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
View Solution
