An uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
The correct Answer is:A
To solve the problem of determining the rate at which energy is stored in a capacitor connected in series with a resistor and a battery, we can follow these steps:
Step 1: Understand the Circuit
We have a capacitor (C) connected in series with a resistor (R) and a battery (V). Initially, the capacitor is uncharged.
Step 2: Write the Charge Equation
Using Kirchhoff's loop law, we can write the equation for the circuit:
QC−IR=0
Where Q is the charge on the capacitor and I is the current through the circuit.
Step 3: Relate Current to Charge
The current I can be expressed as the rate of change of charge:
I=dQdt
Substituting this into the equation gives:
QC−RdQdt=0
Rearranging this, we find:
dQdt=QRC
Step 4: Solve for Charge as a Function of Time
The solution to this differential equation is:
Q(t)=CV(1−e−t/(RC))
This describes how the charge on the capacitor increases over time.
Step 5: Write the Energy Stored in the Capacitor
The energy U stored in the capacitor is given by:
U=Q22C
Substituting our expression for Q(t):
U(t)=(CV(1−e−t/(RC))22C
This simplifies to:
U(t)=CV22(1−e−t/(RC))2
Step 6: Differentiate Energy with Respect to Time
To find the rate at which energy is stored, we differentiate U(t) with respect to time t:
dUdt=ddt(CV22(1−e−t/(RC))2)
Using the chain rule:
dUdt=CV2(1−e−t/(RC))(ddt(1−e−t/(RC)))
Calculating the derivative:
ddt(1−e−t/(RC))=1RCe−t/(RC)
So,
dUdt=CV2(1−e−t/(RC))(1RCe−t/(RC))
This simplifies to:
dUdt=CV2RC(1−e−t/(RC))e−t/(RC)
Step 7: Analyze the Behavior of the Rate of Energy Storage
As time t increases, e−t/(RC) decreases from 1 to 0, meaning that (1−e−t/(RC)) increases from 0 to 1. Therefore, dUdt will initially increase, reach a maximum, and then decrease as t approaches infinity.
Conclusion
The rate at which energy is stored in the capacitor first increases and then decreases over time.
We have a capacitor (C) connected in series with a resistor (R) and a battery (V). Initially, the capacitor is uncharged.
Using Kirchhoff's loop law, we can write the equation for the circuit:
QC−IR=0
Where Q is the charge on the capacitor and I is the current through the circuit.
The current I can be expressed as the rate of change of charge:
I=dQdt
Substituting this into the equation gives:
QC−RdQdt=0
Rearranging this, we find:
dQdt=QRC
The solution to this differential equation is:
Q(t)=CV(1−e−t/(RC))
This describes how the charge on the capacitor increases over time.
The energy U stored in the capacitor is given by:
U=Q22C
Substituting our expression for Q(t):
U(t)=(CV(1−e−t/(RC))22C
This simplifies to:
U(t)=CV22(1−e−t/(RC))2
To find the rate at which energy is stored, we differentiate U(t) with respect to time t:
dUdt=ddt(CV22(1−e−t/(RC))2)
Using the chain rule:
dUdt=CV2(1−e−t/(RC))(ddt(1−e−t/(RC)))
Calculating the derivative:
ddt(1−e−t/(RC))=1RCe−t/(RC)
So,
dUdt=CV2(1−e−t/(RC))(1RCe−t/(RC))
This simplifies to:
dUdt=CV2RC(1−e−t/(RC))e−t/(RC)
As time t increases, e−t/(RC) decreases from 1 to 0, meaning that (1−e−t/(RC)) increases from 0 to 1. Therefore, dUdt will initially increase, reach a maximum, and then decrease as t approaches infinity.
The rate at which energy is stored in the capacitor first increases and then decreases over time.
Topper's Solved these Questions
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:PAPER 3
Explore 99 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:Part-1 Physics
Explore 15 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:MATHS
Explore 14 Videos
- TEST PAPER 4Book:ALLENChapter:TEST PAPER 4Exercise:PHYSICS
Explore 44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
Two capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionAn Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionBy evaluating ∫i2Rdt,show that when a capacitor is charged by connecting it to a battery through a resistor,the energy dissipated as heat equals the energy stored in the capacitor.
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionThe capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
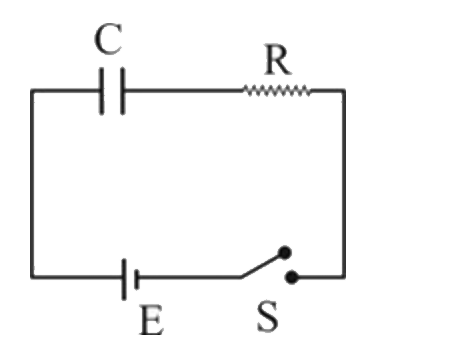
View SolutionThe capacitor C1 in the flgure shown initially carries a charge q0. When the switches S1 and S2 are closed,capacitor C1 is connected in series to a resistor R and a second capacitor C2 which is initially uncharged.
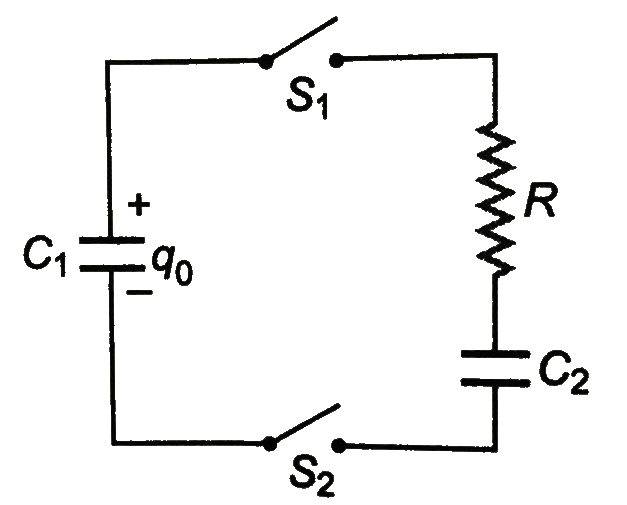
the total heat dissipated in the circuit during the discharging process of C1 is
View SolutionA cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
View SolutionAn uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is
View Solution

