An Uncharged capacitor is connected to a battery through a resistance . Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in .
The correct Answer is:A
To solve the problem, we need to show that the energy dissipated in the resistor R is equal to the energy stored in the capacitor C when it is fully charged. Let's go through the steps systematically.
Step 1: Understand the Circuit
We have a circuit consisting of a battery, a resistor R, and an uncharged capacitor C. When the capacitor is connected to the battery, it begins to charge through the resistor.
Step 2: Energy Stored in the Capacitor
The energy stored in a capacitor when it is fully charged is given by the formula:
UC=12CV2
where V is the voltage of the battery.
Step 3: Charge on the Capacitor
The charge Q on the capacitor when it is fully charged is given by:
Q=CV
Step 4: Total Energy Supplied by the Battery
The total energy supplied by the battery when the capacitor is fully charged is:
UB=Q⋅V=(CV)⋅V=CV2
Step 5: Energy Dissipated in the Resistor
The energy dissipated in the resistor R can be found by subtracting the energy stored in the capacitor from the total energy supplied by the battery:
UR=UB−UC
Substituting the expressions we derived:
UR=CV2−12CV2=12CV2
Step 6: Compare Energy Dissipated and Stored
From the previous steps, we have:
- Energy stored in the capacitor: UC=12CV2
- Energy dissipated in the resistor: UR=12CV2
Thus, we can conclude:
UR=UC
Conclusion
The energy dissipated in the resistor R is equal to the energy stored in the capacitor C when it is fully charged.
---
We have a circuit consisting of a battery, a resistor R, and an uncharged capacitor C. When the capacitor is connected to the battery, it begins to charge through the resistor.
The energy stored in a capacitor when it is fully charged is given by the formula:
UC=12CV2
where V is the voltage of the battery.
The charge Q on the capacitor when it is fully charged is given by:
Q=CV
The total energy supplied by the battery when the capacitor is fully charged is:
UB=Q⋅V=(CV)⋅V=CV2
The energy dissipated in the resistor R can be found by subtracting the energy stored in the capacitor from the total energy supplied by the battery:
UR=UB−UC
Substituting the expressions we derived:
UR=CV2−12CV2=12CV2
From the previous steps, we have:
- Energy stored in the capacitor: UC=12CV2
- Energy dissipated in the resistor: UR=12CV2
UR=UC
The energy dissipated in the resistor R is equal to the energy stored in the capacitor C when it is fully charged.
Topper's Solved these Questions
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- CAPACITORSBook:DC PANDEY ENGLISHChapter:CAPACITORSExercise:OBJECTIVE_TYPE
Explore 1 Video
- ATOMSBook:DC PANDEY ENGLISHChapter:ATOMSExercise:MEDICAL ENTRANCES GALLERY
Explore 42 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
Similar Questions
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionAn uncharged capacitor is connected to a battery. Show that half the energy supplied by the battery is lost as heat while charging the capacitor.
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionAt the trophic level of consumers, the rate at which food energy is assimilarted, is called ?
View SolutionAn uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is
View SolutionThree uncharged capacitors are connected across a battery as shown. It is known that the energy stored in all the capacitors is same. Which of the following is not correct?

View SolutionA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
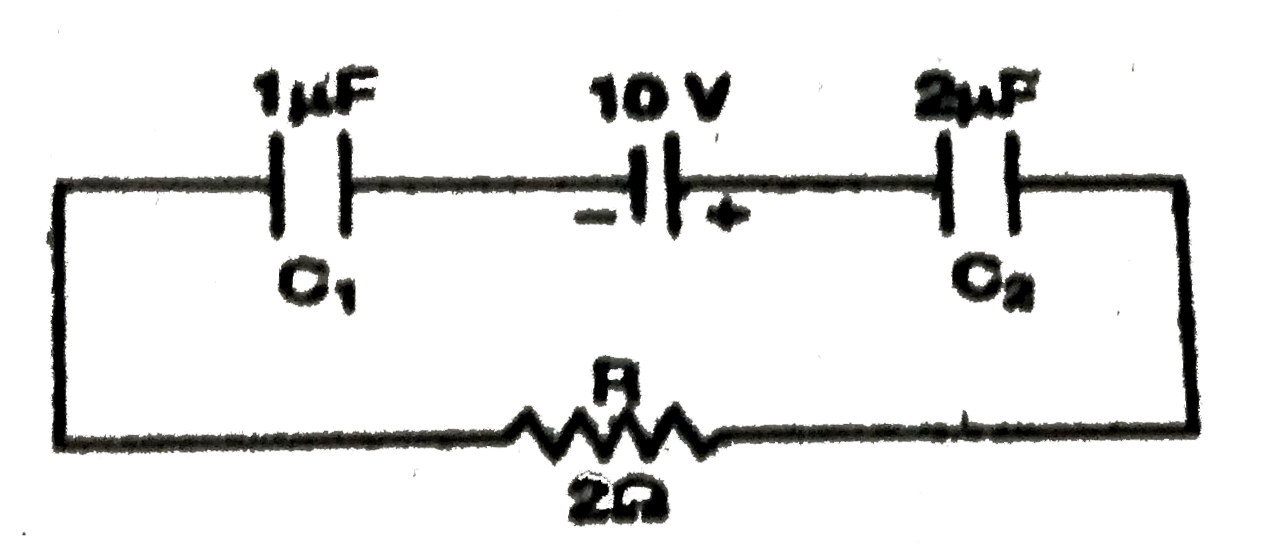
View Solution