Three capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?
The correct Answer is:A, B
To solve the problem step by step, we will address each part of the question systematically.
Given:
- Capacitors: C1=8.4μF, C2=8.4μF, C3=4.2μF
- Voltage across the capacitors: V=36V
(a) Charge on the 4.2μF capacitor
1. Calculate the equivalent capacitance for capacitors in series:
1Ceq=1C1+1C2+1C3
1Ceq=18.4+18.4+14.2
1Ceq=18.4+18.4+28.4=48.4=24.2
Ceq=2.1μF
2. Calculate the total charge Q on the equivalent capacitor:
Q=Ceq×V=2.1μF×36V=75.6μC
3. Since the charge is the same on all capacitors in series, the charge on the 4.2μF capacitor is:
Q4.2=75.6μC
(b) Total energy stored in all three capacitors
1. Use the formula for energy stored in a capacitor:
U=12CeqV2
U=12×2.1×10−6F×(36V)2
U=12×2.1×10−6×1296
U=1.36mJ
(c) Voltage across each capacitor in the parallel combination
1. When the capacitors are disconnected and reconnected in parallel, the charge on each capacitor remains the same:
- Charge on C1 and C2: Q1=Q2=75.6μC
- Charge on C3: Q3=75.6μC
2. Calculate the voltage across each capacitor using V=QC:
- For C1 and C2:
V1=V2=Q1C1=75.6μC8.4μF=9V
- For C3:
V3=Q3C3=75.6μC4.2μF=18V
(d) Total energy now stored in the capacitors
1. Calculate the total energy stored in the parallel combination:
Utotal=12C1V21+12C2V22+12C3V23
Utotal=12×8.4×10−6×(9)2+12×8.4×10−6×(9)2+12×4.2×10−6×(18)2
Utotal=2×12×8.4×10−6×81+12×4.2×10−6×324
Utotal=0.0003402+0.0006804=1.02mJ
Summary of Answers:
(a) Charge on 4.2μF capacitor: 75.6μC
(b) Total energy stored: 1.36mJ
(c) Voltage across each capacitor in parallel: 9V for C1 and C2, 18V for C3
(d) Total energy in parallel: 1.02mJ
- Capacitors: C1=8.4μF, C2=8.4μF, C3=4.2μF
- Voltage across the capacitors: V=36V
1Ceq=1C1+1C2+1C3
1Ceq=18.4+18.4+14.2
1Ceq=18.4+18.4+28.4=48.4=24.2
Ceq=2.1μF
Q=Ceq×V=2.1μF×36V=75.6μC
Q4.2=75.6μC
U=12CeqV2
U=12×2.1×10−6F×(36V)2
U=12×2.1×10−6×1296
U=1.36mJ
- Charge on C1 and C2: Q1=Q2=75.6μC
- Charge on C3: Q3=75.6μC
- For C1 and C2:
V1=V2=Q1C1=75.6μC8.4μF=9V
- For C3:
V3=Q3C3=75.6μC4.2μF=18V
Utotal=12C1V21+12C2V22+12C3V23
Utotal=12×8.4×10−6×(9)2+12×8.4×10−6×(9)2+12×4.2×10−6×(18)2
Utotal=2×12×8.4×10−6×81+12×4.2×10−6×324
Utotal=0.0003402+0.0006804=1.02mJ
(a) Charge on 4.2μF capacitor: 75.6μC
(b) Total energy stored: 1.36mJ
(c) Voltage across each capacitor in parallel: 9V for C1 and C2, 18V for C3
(d) Total energy in parallel: 1.02mJ
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
The energy stored in 4μF capacitors is
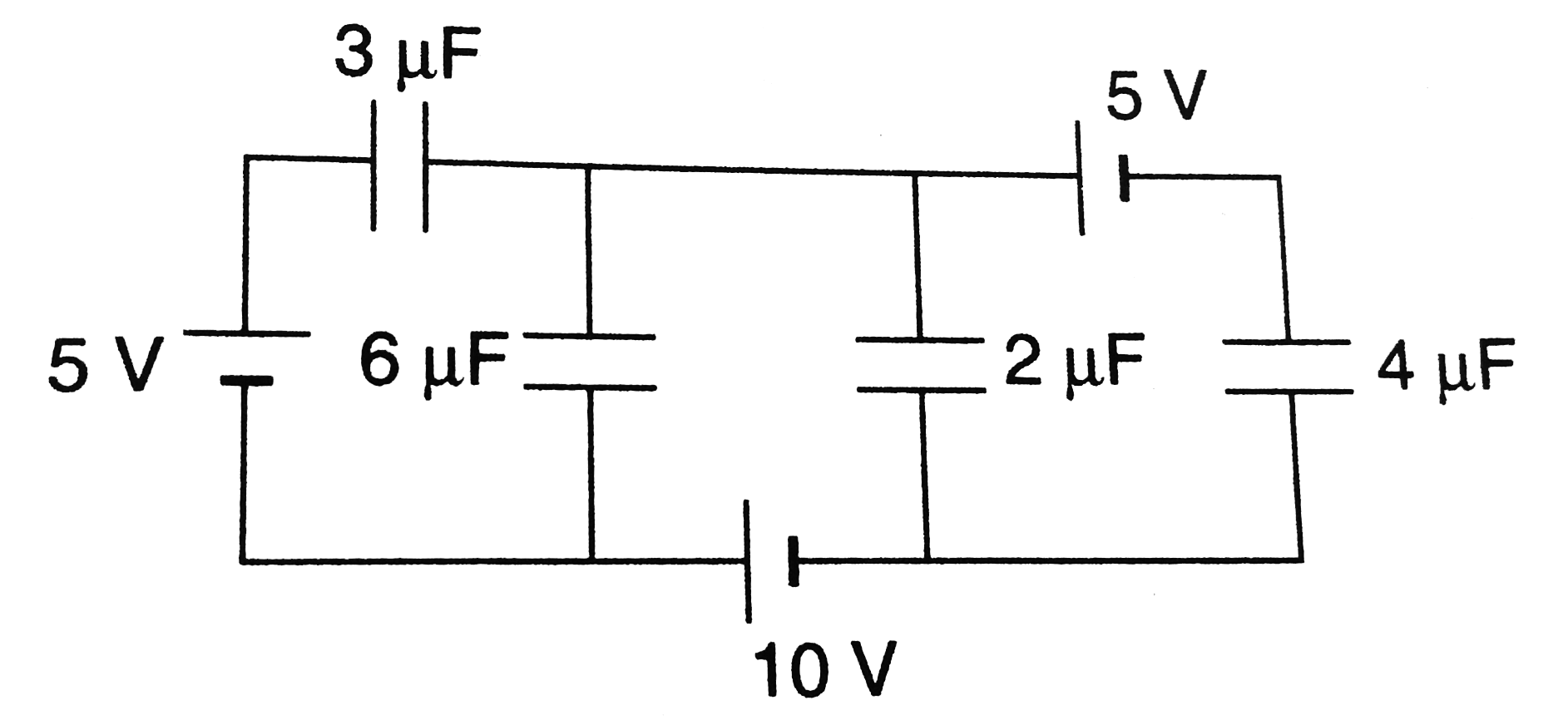
View SolutionFind the charges on 6μF and 4μF capacitors
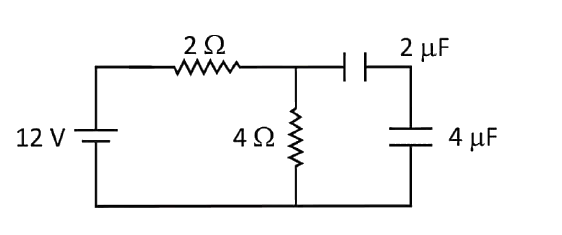
View SolutionThe charge on the 4μF capacitor in the steady state is
View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
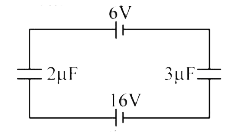
View SolutionWhat is the potential difference across 2μF capacitor in the circuit shown?
View SolutionFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
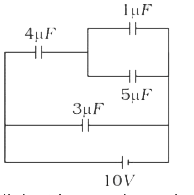
View SolutionThe charge on the 4μF capacitor at steady state is (in μC)
View SolutionFigure shows five capacitors connected across a 12V power supply. What is the charge on the 2μF capacitor ?

View SolutionIf potential difference across 3μF is 4V, then total energy stored in all capacitors is
View SolutionThree capacitors having capanctances 20μF,30μF and 40μF are conneceted in series with a 12V battary. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
View Solution

