Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
The energy stored in the capacitor is <br>U = (1)/(2) CV^2 = (1)/(2) (100 mu F) (20 V)^2 = 0.02 J<br>. The energy stored in a capacitor is electrostatic potential energy. When we pull the plates of a capacitor apart, we have to do work against the electrostatic attraction between the plates. In which region of space is the energy stored ? When we increase the separation between the plates from <br>d_1 to d_2<br>, an amount<br>(Q)^2/(2A epsilon_0) (d_2 - d_1)<br> of work is performed by us and The field due to the charges <br>Q_p, - Q_p<br> is directed oppositely and has magnitude <br>E_p =(sigma_p )/(epsilon_o) =(Q_p)/(Aepsilon_o)<br>. The resultant field is <br> E = E_0 - E_p<br> = (Q-Q_p)/(A epsilon_0)<br>. From equations (ii) and (iii), (Q - Q_p)/(epsilon_o A) = (Q)/(epsilon _o AK)<br> or, <br>Q - Q_p = (O)/(K)<br> or, <br>Q_p = Q (1 -(1)/(K)).

Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - worked out examples
23 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Objective 1
12 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA capacitor of capacitor of capacitance 2.0μF is charge to a potential diffrence of 12V It is then connected of uncharged capacitor of capacitance 4.0μF as shown in figure . Find (a ) the charge on each of the two capacitors after the connection, (b ) the electrostatic energy stored in each of the two capacitors.

View SolutionA 100μF capacitor is charged to a potential difference of 24V. It is connected to an uncharged capacitor of capacitance 20μF What will be the new potential difference across the 100μF capacitor?
View SolutionCalculate the energy stored in the capacitor of capacitance 2μf. The voltmeter gives a reading of 15 V and the ammeter A reads 15mA .
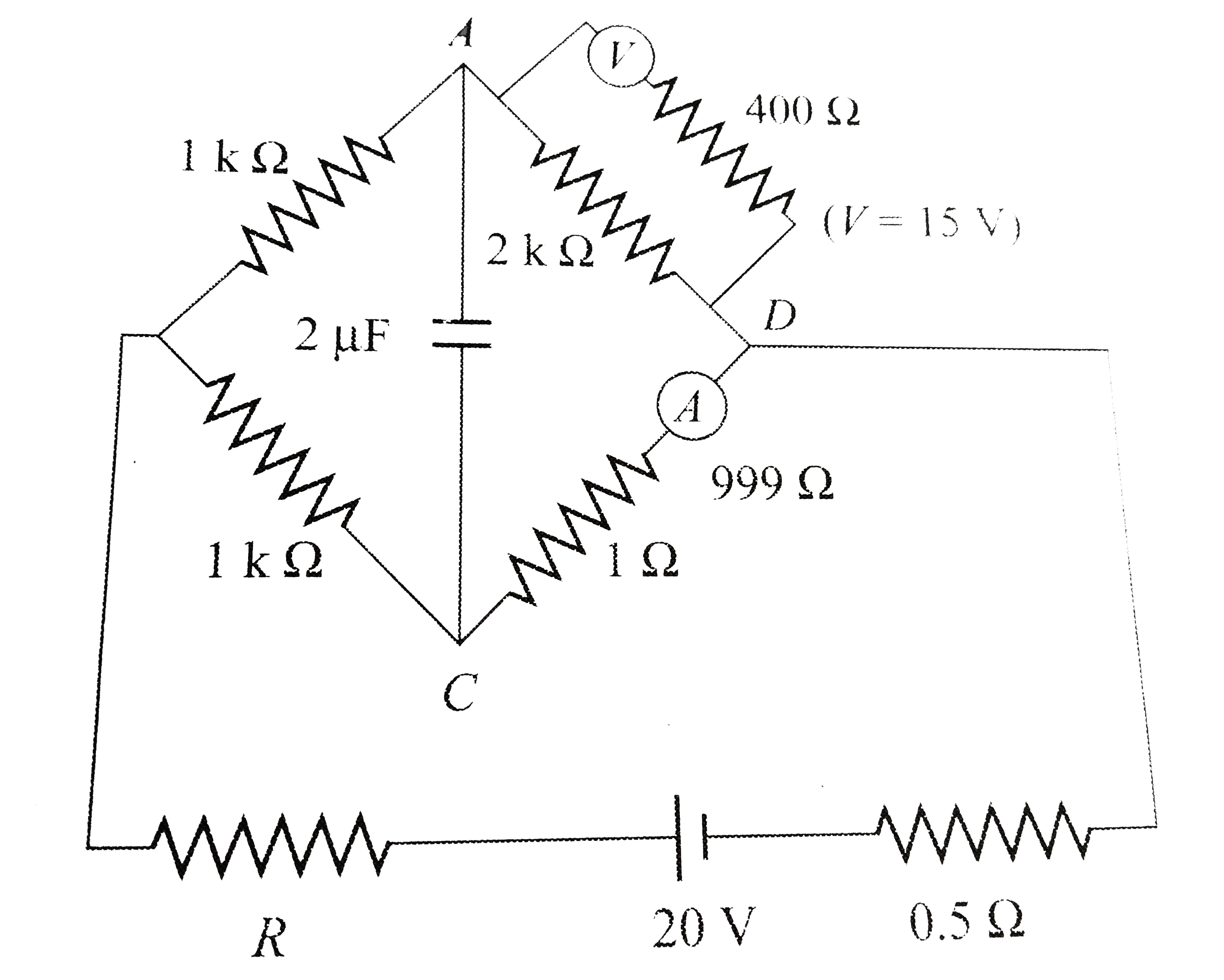
View SolutionA radioactive sample decays with a mean life of 20ms. A capacitor of capacitance 100μF is charged to some potential and then the plates are connected to a resistance .R.. If the ratio of the charge on the capacitance to the activity of radioactive sample remains constant in time is R=100(x)Ω, then x=
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
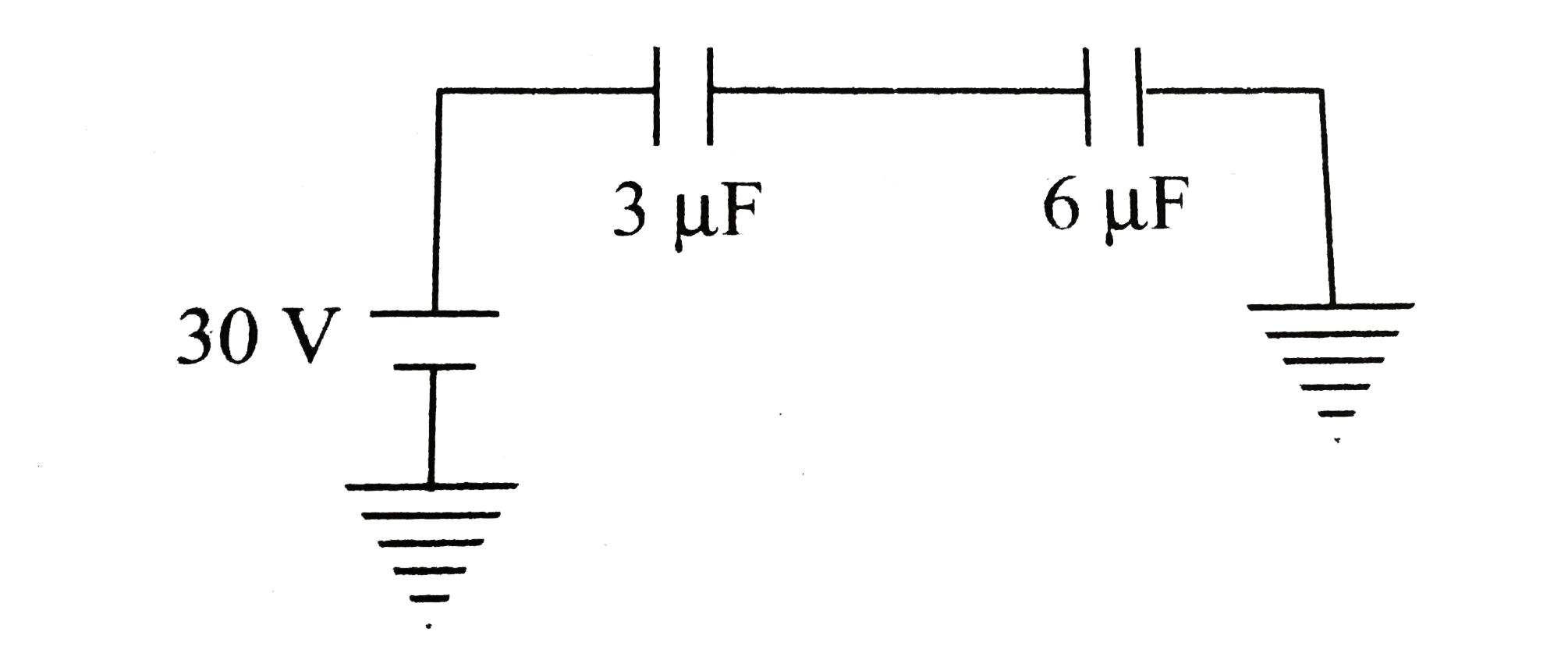
View Solution

