A capacitor of capacitor of capacitance 2.0μF is charge to a potential diffrence of 12V It is then connected of uncharged capacitor of capacitance 4.0μF as shown in figure . Find (a ) the charge on each of the two capacitors after the connection, (b ) the electrostatic energy stored in each of the two capacitors.

Initail charge stored
C×V=12×2×10−6
=24×10−6C
Let the charged on 2μF and 4μf capacitance be q1 and q2 respectively
Here , q2=2q1
or , q_1 + q_2 = 24 xx 10^(-6) <br>rArr 3 q_1 = 24 xx 10^(-6) C <br> q_1 = 8 xx 10^(-6) C = 8 mu C <br>q_1 = 2 q_1 = 16 mu C<br>E_1 = 1 /2 xx C_1 v_2^(2) = 16 mu J<br>E_2 = 1 / 2 xx C_2 v_2^(2) = 32 mu J.
Topper's Solved these Questions
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:short answer
Explore 7 Videos
- CAPACITORSBook:HC VERMA ENGLISHChapter:CAPACITORSExercise:OBJECTIVE 2
Explore 6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBook:HC VERMA ENGLISHChapter:BOHR'S MODEL AND PHYSICS OF THE ATOMExercise:Short Answer
Explore 10 Videos
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Question for short Answer
Explore 6 Videos
Similar Questions
A capacitor of capacitance 2.0μF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4.0μF. Find (a) the charge flow through connecting wire upto study strate on each of the two capacitors after the connection in μC (b) The total electrostatic energy stored in both capacitors in μJ (c) the heat produced during the charge transfer from one capacitor to the other in μJ.
View SolutionA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
View Solution
Knowledge Check
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
View SolutionA capacitor of 0.75μF is charged to a voltage of 16 V. What is the magnitude of the charge on each plate of the capacitor ?
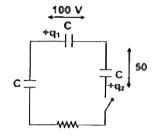
View SolutionTwo capacitor each of capacitance C=1μF each charged to potential 100 V and 50 V respectively and connected across a uncharged capacitor 'C' = 1μF as shown in the figure if switch 'S' is closed then charge in the uncharged capacitor at equilibrium will be
View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionA 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
View Solution

