The two square faces of a rectangular dielectric slab (dielectric constant4.0) of dimensions 20cm x20cm x 1.0mm are metal -coated. Find the capacitance between the coated surfaces.
To find the capacitance between the coated surfaces of a rectangular dielectric slab, we can follow these steps:
1. Identify the Given Values:
- Dielectric constant (K) = 4.0
- Dimensions of the slab: Length = 20 cm, Width = 20 cm, Thickness = 1.0 mm
- Convert dimensions to meters for standard SI units:
- Length = 20 cm = 0.20 m
- Width = 20 cm = 0.20 m
- Thickness = 1.0 mm = 0.001 m
2. Calculate the Area (A):
- The area of the coated surfaces (which are square) is given by:
A=Length×Width=0.20m×0.20m=0.04m2
3. Use the Formula for Capacitance (C):
- The formula for the capacitance of a parallel plate capacitor with a dielectric is:
C=ϵ0⋅K⋅AD
- Where:
- ϵ0 (Permittivity of free space) = 8.85×10−12F/m
- K = Dielectric constant = 4.0
- A = Area = 0.04m2
- D = Distance between the plates = 0.001m
4. Substitute the Values into the Formula:
- Plugging in the values:
C=(8.85×10−12)⋅4.0⋅0.040.001
5. Calculate the Capacitance:
- First, calculate the numerator:
8.85×10−12⋅4.0⋅0.04=1.416×10−12F
- Now divide by D:
C=1.416×10−120.001=1.416×10−9F
6. Convert to Microfarads:
- To convert farads to microfarads:
C=1.416×10−9F=1.416nF=0.001416μF
Final Answer:
The capacitance between the coated surfaces is approximately 1.416nF or 0.001416μF.
- Dielectric constant (K) = 4.0
- Dimensions of the slab: Length = 20 cm, Width = 20 cm, Thickness = 1.0 mm
- Convert dimensions to meters for standard SI units:
- Length = 20 cm = 0.20 m
- Width = 20 cm = 0.20 m
- Thickness = 1.0 mm = 0.001 m
- The area of the coated surfaces (which are square) is given by:
A=Length×Width=0.20m×0.20m=0.04m2
- The formula for the capacitance of a parallel plate capacitor with a dielectric is:
C=ϵ0⋅K⋅AD
- Where:
- ϵ0 (Permittivity of free space) = 8.85×10−12F/m
- K = Dielectric constant = 4.0
- A = Area = 0.04m2
- D = Distance between the plates = 0.001m
- Plugging in the values:
C=(8.85×10−12)⋅4.0⋅0.040.001
- First, calculate the numerator:
8.85×10−12⋅4.0⋅0.04=1.416×10−12F
- Now divide by D:
C=1.416×10−120.001=1.416×10−9F
- To convert farads to microfarads:
C=1.416×10−9F=1.416nF=0.001416μF
The capacitance between the coated surfaces is approximately 1.416nF or 0.001416μF.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
Knowledge Check
A piece of paper of dimensions 1.5 m x 20 cm has area :
A30m2B300cm2C0.3m2D3000m3
A parallel-plate of capacitor of capacitance 5μF is connected in a battery of emf 6V. The separation between the plate is 2mm.(a) Find the charge on the positive plate.(b) find the eletric field between the plate.(c) A dielectric slab of thickness 1 mm and dielectric constant 5 is inserted into the gap to occupy the lower half of it.Find the capacitance of the new combination .(d)How much charge has flow n through the battery after the slab is inserted?
View SolutionA capacitor having a capacitance of 100μf is changed to a potential difference of 50V.(a) What is the magnitude of the charge on each plate? (b)The charging battery is disconnected and a dielectric of dielectric constant 2.5 is inserted . Calculate the new potential difference between the plate .(c) What charge would have produced this potential difference in absence of the dielectric slab.(d) Find the charge induced at a surface of the dielectric slab.
View SolutionA parallel plate capacitor without any dielectric has capacitance C0. A dielectric slab is made up of two dielectric slabs of dielectric constants K and 2K and is of same dimensions as that of capacitor plates and both the parts are of equal dimensions arranged serially as shown. If this dielectric slab is introduced (dielectric K enters first) in between the plates at constant speed, then variation of capacitance with time will be best represented by :

View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
View SolutionA paller- plate capacitor has plate area 100cm2 and plate separation 1.0cm.A glass plate (dielectric constant 4.0)are inserted one over the other the fill the space between the plate of the capacitor.Find the new capacitance.
View SolutionThe two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adjusted that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
View SolutionTwo parallel plate capacitors A and B have the same separation d=8.85×10−4m between the plates. The plate area of A and B are 0.04m2 and 0.02m2 respectively. A slab of dielectric constant (relative permittivity) K=9 has dimensions such that it can exactly fill the space between the plates of capacitor B.
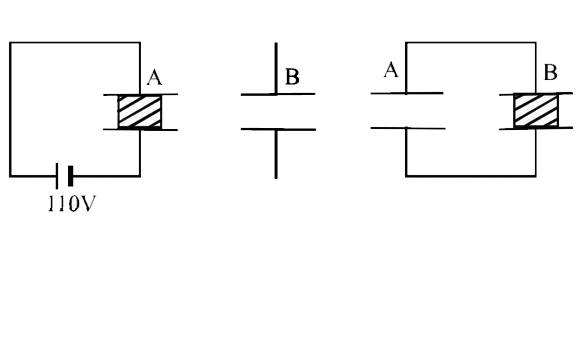
(i) The dielectric slab is placed inside. A as shown in figure (a). A is then charged to a potential difference of 110V. Calculate the capacitance of A and the energy stored in it.
The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely, The two capacitors A and B are then connected as shown in figure(c). Calculate the energy stored in the system.
View Solution

