Two parallel plate capacitors A and B have the same separation between the plates. The plate area of A and B are and respectively. A slab of dielectric constant (relative permittivity) has dimensions such that it can exactly fill the space between the plates of capacitor B.
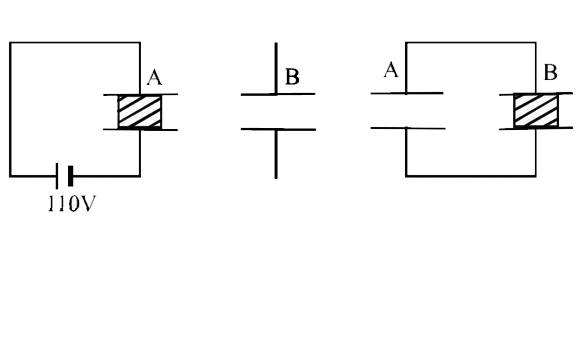
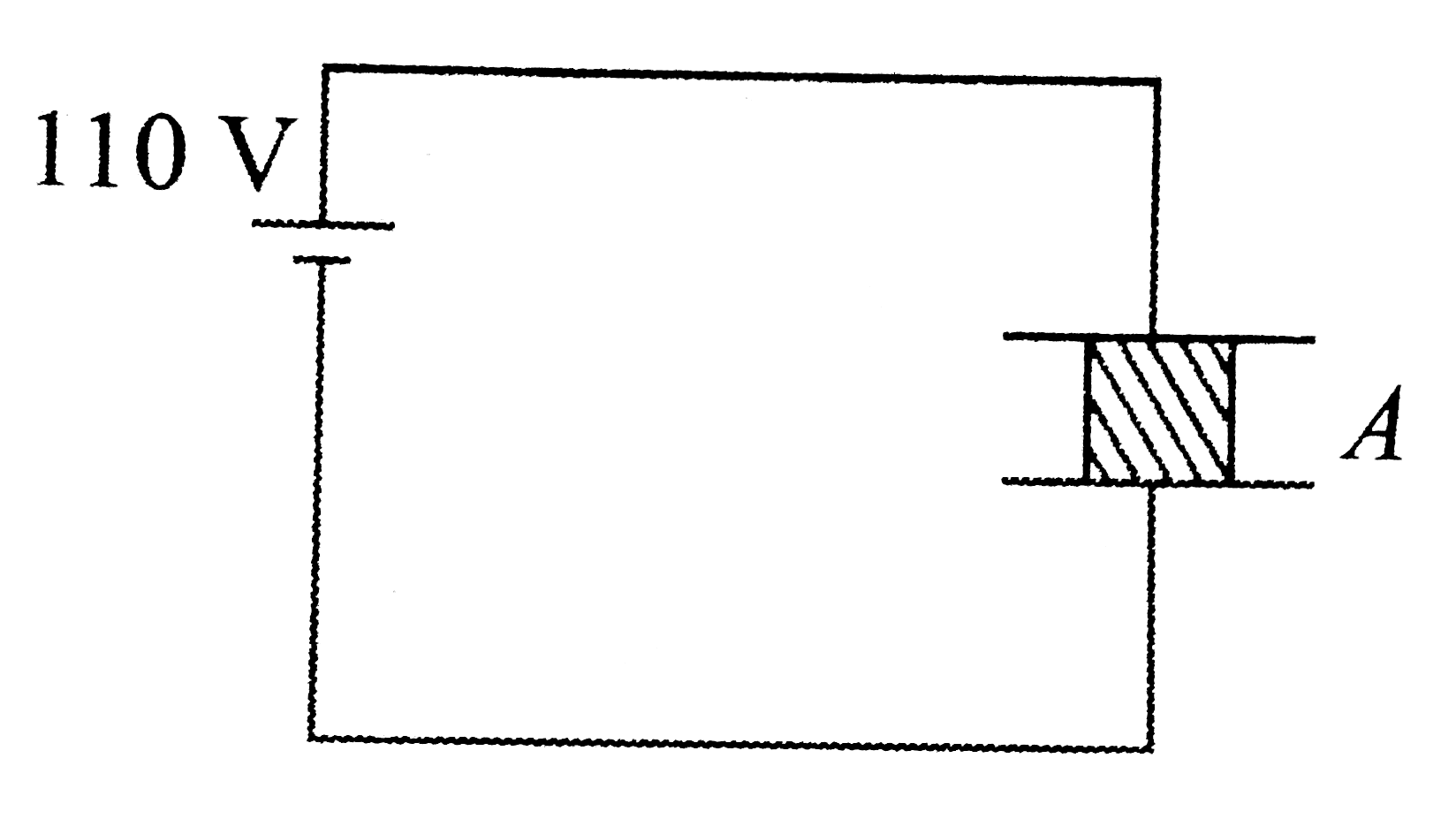
(i) The dielectric slab is placed inside. A as shown in figure (a). A is then charged to a potential difference of 110V. Calculate the capacitance of A and the energy stored in it.
The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely, The two capacitors A and B are then connected as shown in figure(c). Calculate the energy stored in the system.
Capacitor with a dielectric
 . Can be regarded as two capacitors in parallel, one having a dielectric and the other having no dielectric stare. Such a capacitor has an area of . So the combined capacitace is
. Can be regarded as two capacitors in parallel, one having a dielectric and the other having no dielectric stare. Such a capacitor has an area of . So the combined capacitace is
Thus, energy stored is
Work done in removing the dielectric state =(Energy stored in capacitor without dielectric)-(Energy stored in capacitor with dielectric)
It may be noted that on taking out the dielectric, the charge on the capacitor plate remains the same.
Here,
,
q=CV=2xx10^(-9)xx110=2.2xx10^(-7) C:. W=(2.2xx10^(-7))^(2)/2[1/(0.4xx10^(-9))1/(2xx10^(-9)]]=4.84xx10^(-5)Jepsilon_(0)KA_(B)//dC_(B)=1.8xx18^(9) FA,q_(A)=2.2xx10^(-7) C,q_(1)q_(2)q_(1)+q_(2)=2.2xx10^(-7) Cq_(1)/C_(A)=q_(2)/C_(B)q_(1)=C_(A)/C_(B)q_(2) =(0.4xx10^(-9))/(1.8xx10^(-9))q_(2)=0.22q_(2)0.22q_(2)+q_(2)=2.2xx10^(-7)q_(2)=(2.2)/(1.22)xx10^(-7) =1.8xx10^(-7) Cq_(1)=0.4xx10^(-7) Cq_(1)^(2)/(2C_(A))+q_(1)^(2)/(2C_(B)) =0.2xx10^(-5)+0.9xx10^(-5)=1.1xx10^(-5) JQ^(2)//2C_(eq).
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Exercise 4.1
Explore 13 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Exercise 4.2
Explore 32 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
A parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionA parallel plate capacitor of capacitance C (without dielectric) is filled by dielectric slabs as shown in figure. Then the new capacitance of the capacitor is

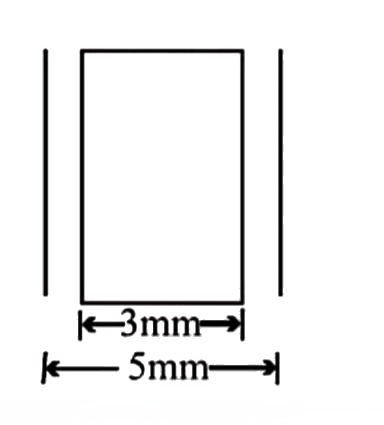
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionThe space between the plates of a parallel plate capacitor of capacitance C is filled with three dielectric slabs of identical size as shown in figure. If the dielectric constants of the three slabs are K1,K2andK3 find the new capacitance.

View SolutionA paller- plate capacitor has plate area 100cm2 and plate separation 1.0cm.A glass plate (dielectric constant 4.0)are inserted one over the other the fill the space between the plate of the capacitor.Find the new capacitance.
View SolutionFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the gaps between the plates and the electric slab will be
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionThe plates of a parallel plate capacitor are charged up to 200 V. A dielectric slab of thickness 4 mm is inserted between its plates. Then, to maintain the same potential difference between the plates of the capacitor, the distance between the plates increased by 3.2 mm. The dielectric constant of the dielectric slab is
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View Solution
