Find the capacitance between the terminals A and C3 If εr=2
To find the capacitance between terminals A and C3 (which is actually point B), we will follow these steps:
Step 1: Understand the Configuration
We have two capacitor plates with a distance D between them and an area A. The relative permittivity of the medium is given as ϵr=2.
Step 2: Identify the Capacitance Formula
The capacitance C of a parallel plate capacitor is given by the formula:
C=ϵAd
where ϵ is the permittivity of the medium, A is the area of the plates, and d is the distance between the plates.
Step 3: Calculate Capacitance for Each Section
1. For C1: The area is A/2 and the distance is D:
C1=ϵ0A/2D=Aϵ02D
2. For C2: The area is A/2 and the distance is D/2:
C2=ϵ0A/2D/2=Aϵ0D
3. For C3: The area is A and the distance is D/2 with the relative permittivity ϵ=ϵ0ϵr=2ϵ0:
C3=2ϵ0AD/2=4Aϵ0D
Step 4: Combine Capacitances
C2 and C3 are in series. The equivalent capacitance Ceq of capacitors in series is given by:
1Ceq=1C2+1C3
Substituting the values:
1Ceq=DAϵ0+D4Aϵ0
Finding a common denominator:
1Ceq=4D4Aϵ0+D4Aϵ0=5D4Aϵ0
Thus,
Ceq=4Aϵ05D
Step 5: Total Capacitance
Now, we add C1 (which is in parallel with Ceq):
Ctotal=C1+Ceq=Aϵ02D+4Aϵ05D
Finding a common denominator (which is 10D):
Ctotal=5Aϵ010D+8Aϵ010D=13Aϵ010D
Step 6: Final Expression
Thus, the final capacitance between terminals A and C3 is:
C=13Aϵ010D
We have two capacitor plates with a distance D between them and an area A. The relative permittivity of the medium is given as ϵr=2.
The capacitance C of a parallel plate capacitor is given by the formula:
C=ϵAd
where ϵ is the permittivity of the medium, A is the area of the plates, and d is the distance between the plates.
1. For C1: The area is A/2 and the distance is D:
C1=ϵ0A/2D=Aϵ02D
C2=ϵ0A/2D/2=Aϵ0D
C3=2ϵ0AD/2=4Aϵ0D
C2 and C3 are in series. The equivalent capacitance Ceq of capacitors in series is given by:
1Ceq=1C2+1C3
Substituting the values:
1Ceq=DAϵ0+D4Aϵ0
Finding a common denominator:
1Ceq=4D4Aϵ0+D4Aϵ0=5D4Aϵ0
Thus,
Ceq=4Aϵ05D
Now, we add C1 (which is in parallel with Ceq):
Ctotal=C1+Ceq=Aϵ02D+4Aϵ05D
Finding a common denominator (which is 10D):
Ctotal=5Aϵ010D+8Aϵ010D=13Aϵ010D
Thus, the final capacitance between terminals A and C3 is:
C=13Aϵ010D
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.1
13 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.2
32 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
Find the equivalent capacitance between terminals A and B.
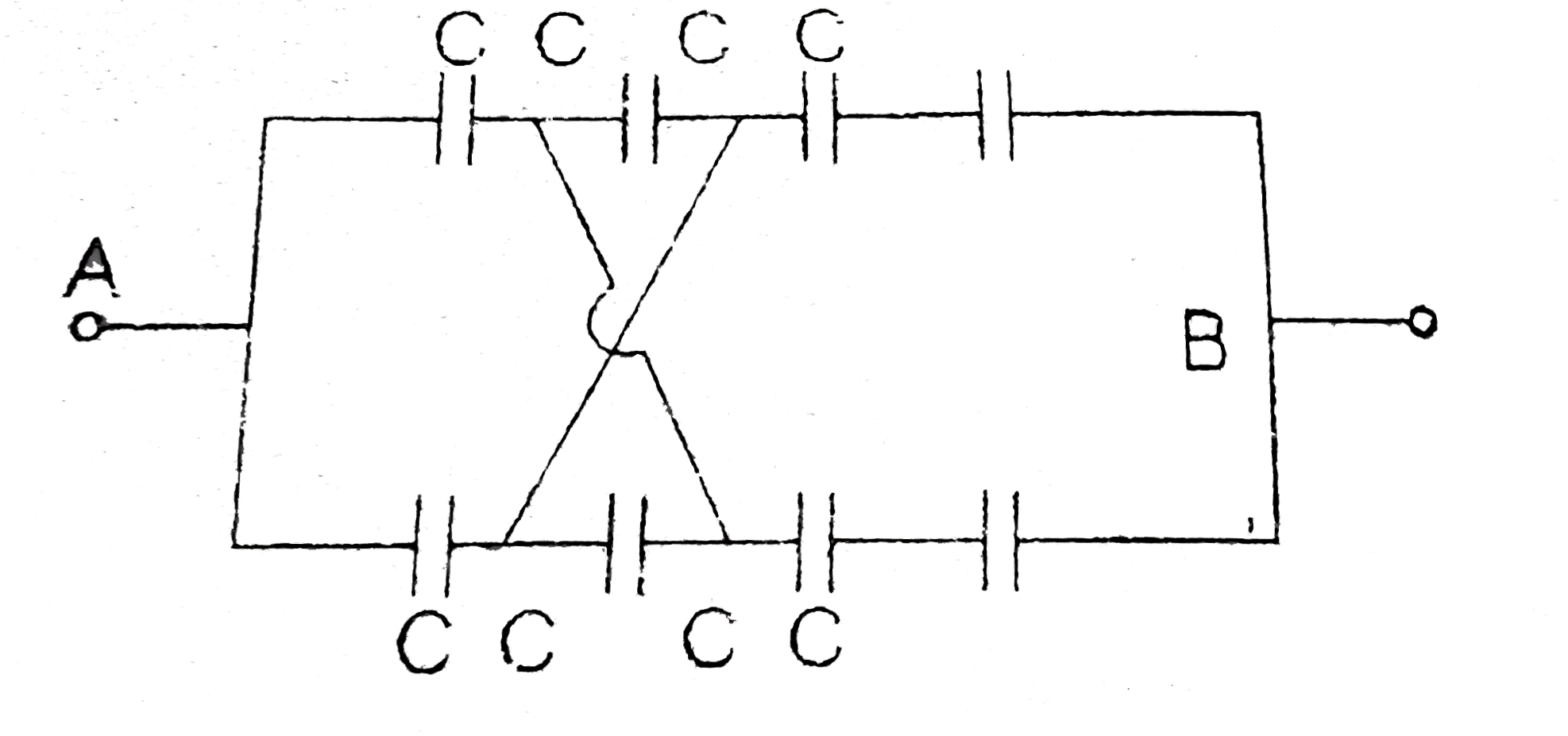
View SolutionFind equivalent capacitance between points A and B

View SolutionFind equivalent capacitance between points A and B,

View SolutionFind equivalent capacitance between A and B
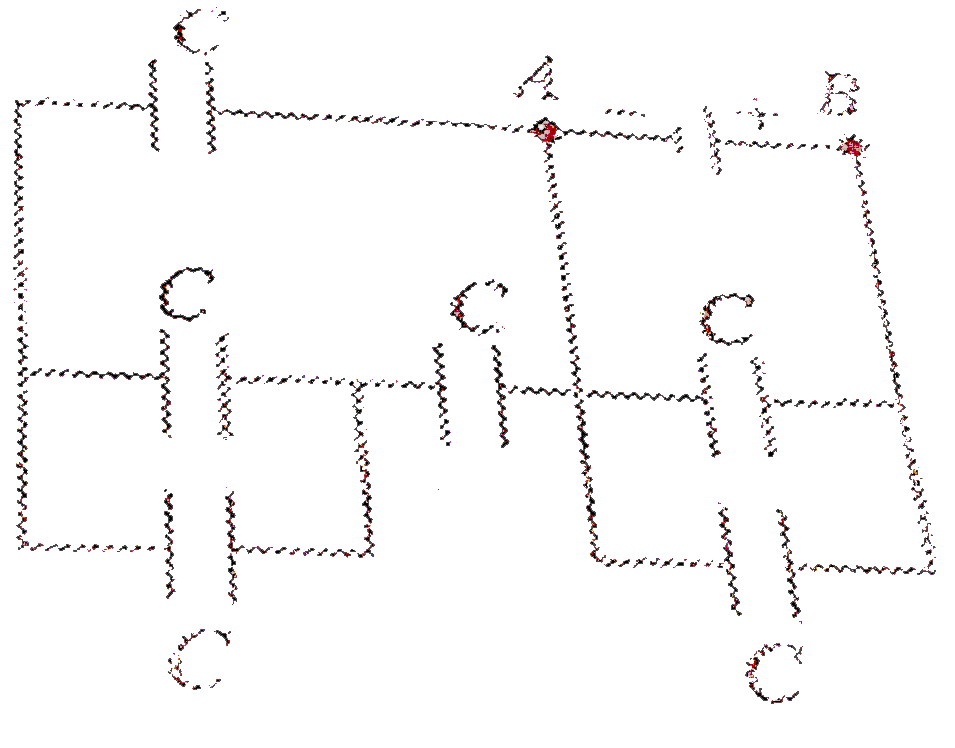
View SolutionFind the equivalent capacitance between point A and B .
View SolutionTwo balls, each of radius R, equal mass and density, are placed in contact. Then the force of gravitation between them is proportional to:
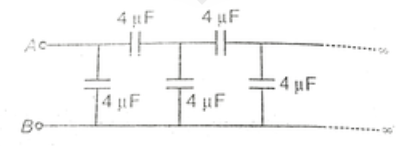
View SolutionFind the equivalent capacitance between A and B

View SolutionFind the equivalent capacitance between A and B
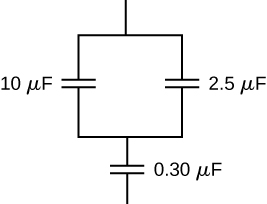
View SolutionFind the capacitance between the point A and B of the given assemblies.

View SolutionFind the equivalent capacitance between C and B.
View Solution
