A large conducting plane has a surface charge density 1.0x10−4Cm−2 . Find the electrostatic energy stored in a cubical volume of edge 1 cm in the front plane.
To solve the problem of finding the electrostatic energy stored in a cubical volume of edge 1 cm in front of a large conducting plane with a surface charge density of 1.0×10−4C/m2, we can follow these steps:
1. Identify Given Data:
- Surface charge density, σ=1.0×10−4C/m2
- Edge of the cube, A=1cm=0.01m
2. Convert Edge Length to Meters:
- Since the surface charge density is in C/m2, convert the edge length of the cube from centimeters to meters:
A=1cm=0.01m
3. Calculate the Electric Field (E) due to the Conducting Plane:
- The electric field E due to an infinite conducting plane with surface charge density σ is given by:
E=σϵ0
- Where ϵ0 (the permittivity of free space) is approximately 8.854×10−12C2/N m2.
4. Substitute the Values to Find E:
E=1.0×10−48.854×10−12≈1.13×107N/C
5. Calculate the Electrostatic Energy per Unit Volume:
- The formula for electrostatic energy stored per unit volume u is:
u=12ϵ0E2
- Substitute E into the equation:
u=12×8.854×10−12×(1.13×107)2
6. Calculate E2:
E2=(1.13×107)2≈1.2769×1014(N/C)2
7. Substitute E2 into the Energy Formula:
u=12×8.854×10−12×1.2769×1014
u≈5.66×102J/m3
8. Calculate the Volume of the Cube:
- The volume V of the cube is given by:
V=A3=(0.01)3=1.0×10−6m3
9. Calculate the Total Electrostatic Energy Stored in the Cube:
U=u⋅V=5.66×102×1.0×10−6
U≈5.66×10−4J
Final Answer:
Thus, the electrostatic energy stored in the cubical volume is approximately:
U≈5.66×10−4J
- Surface charge density, σ=1.0×10−4C/m2
- Edge of the cube, A=1cm=0.01m
- Since the surface charge density is in C/m2, convert the edge length of the cube from centimeters to meters:
A=1cm=0.01m
- The electric field E due to an infinite conducting plane with surface charge density σ is given by:
E=σϵ0
- Where ϵ0 (the permittivity of free space) is approximately 8.854×10−12C2/N m2.
E=1.0×10−48.854×10−12≈1.13×107N/C
- The formula for electrostatic energy stored per unit volume u is:
u=12ϵ0E2
- Substitute E into the equation:
u=12×8.854×10−12×(1.13×107)2
E2=(1.13×107)2≈1.2769×1014(N/C)2
u=12×8.854×10−12×1.2769×1014
u≈5.66×102J/m3
- The volume V of the cube is given by:
V=A3=(0.01)3=1.0×10−6m3
U=u⋅V=5.66×102×1.0×10−6
U≈5.66×10−4J
Thus, the electrostatic energy stored in the cubical volume is approximately:
U≈5.66×10−4J
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A spherical volume contains a uniformaly distributed charge of density 2.0×10−4Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
View SolutionA large plane sheet of charge having surface charge density 5×10−16cm−2 lies in XY plane. Find electric flux through a circular area of radius 1cm Given normal to the circular area makes an angle of 60∘ with Z-axis.
View Solution
Knowledge Check
A uniformly charged conducting sphere of 4.4 m diameter has a surface change density of 60μCm−2. The charge on the sphere is
A7.3×10−3CB3.7×10−6CC7.3×10−6CD3.7×10−3C
An infinite thin plane sheet of charge density 7.08×10−11(C/m2) is held in air. Find the electric field at a point very close to the sheet.
View SolutionA large plane charge sheet having surface xharge density σ=2.0×10−6Cm−2 lies in the x-y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y, z are all positive and with its normal making an angle of 600 with the z-axis.
View SolutionA uniformly charged conducting sphere is having radius 1 m and surface charge density 20 Cm−2. The total flux leaving the Gaussian surface enclosing the sphere is
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
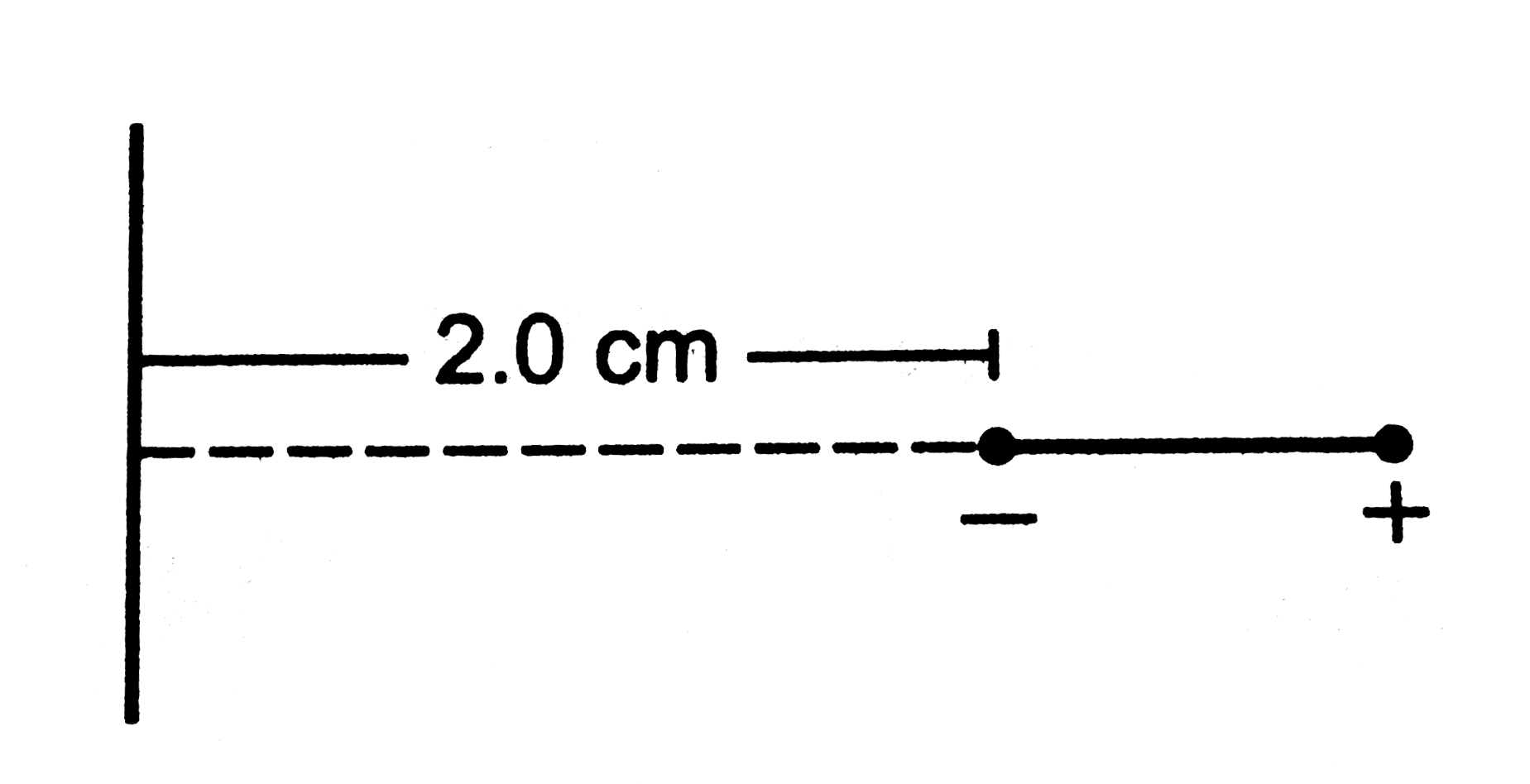
View SolutionA long cylindrical wire carries a positive charge of linear density 2.0 x 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
View Solution
