A spherical volume contains a uniformaly distributed charge of density 2.0×10−4Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
To find the electric field at a point inside a uniformly charged non-conducting spherical volume, we can use the formula derived from Gauss's Law. Here’s a step-by-step solution:
Step 1: Understand the Given Data
We are given:
- Charge density, ρ=2.0×10−4C/m3
- Distance from the center, r=4.0cm=0.04m
Step 2: Use the Formula for Electric Field Inside a Uniformly Charged Sphere
For a uniformly charged non-conducting sphere, the electric field E at a distance r from the center is given by the formula:
E=ρ⋅r3ϵ0
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
Step 3: Substitute the Values into the Formula
Now, substitute the given values into the formula:
E=(2.0×10−4C/m3)⋅(0.04m)3⋅(8.85×10−12C2/N m2)
Step 4: Calculate the Numerator
Calculate the numerator:
2.0×10−4C/m3⋅0.04m=8.0×10−6C/m2
Step 5: Calculate the Denominator
Calculate the denominator:
3⋅(8.85×10−12C2/N m2)=2.655×10−11C2/N m2
Step 6: Divide the Numerator by the Denominator
Now, divide the numerator by the denominator to find the electric field:
E=8.0×10−62.655×10−11≈3.01×105N/C
Step 7: Final Result
Thus, the electric field at a point 4.0 cm from the center of the spherical volume is approximately:
E≈3.0×105N/C
We are given:
- Charge density, ρ=2.0×10−4C/m3
- Distance from the center, r=4.0cm=0.04m
For a uniformly charged non-conducting sphere, the electric field E at a distance r from the center is given by the formula:
E=ρ⋅r3ϵ0
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
Now, substitute the given values into the formula:
E=(2.0×10−4C/m3)⋅(0.04m)3⋅(8.85×10−12C2/N m2)
Calculate the numerator:
2.0×10−4C/m3⋅0.04m=8.0×10−6C/m2
Calculate the denominator:
3⋅(8.85×10−12C2/N m2)=2.655×10−11C2/N m2
Now, divide the numerator by the denominator to find the electric field:
E=8.0×10−62.655×10−11≈3.01×105N/C
Thus, the electric field at a point 4.0 cm from the center of the spherical volume is approximately:
E≈3.0×105N/C
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 2
8 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
Similar Questions
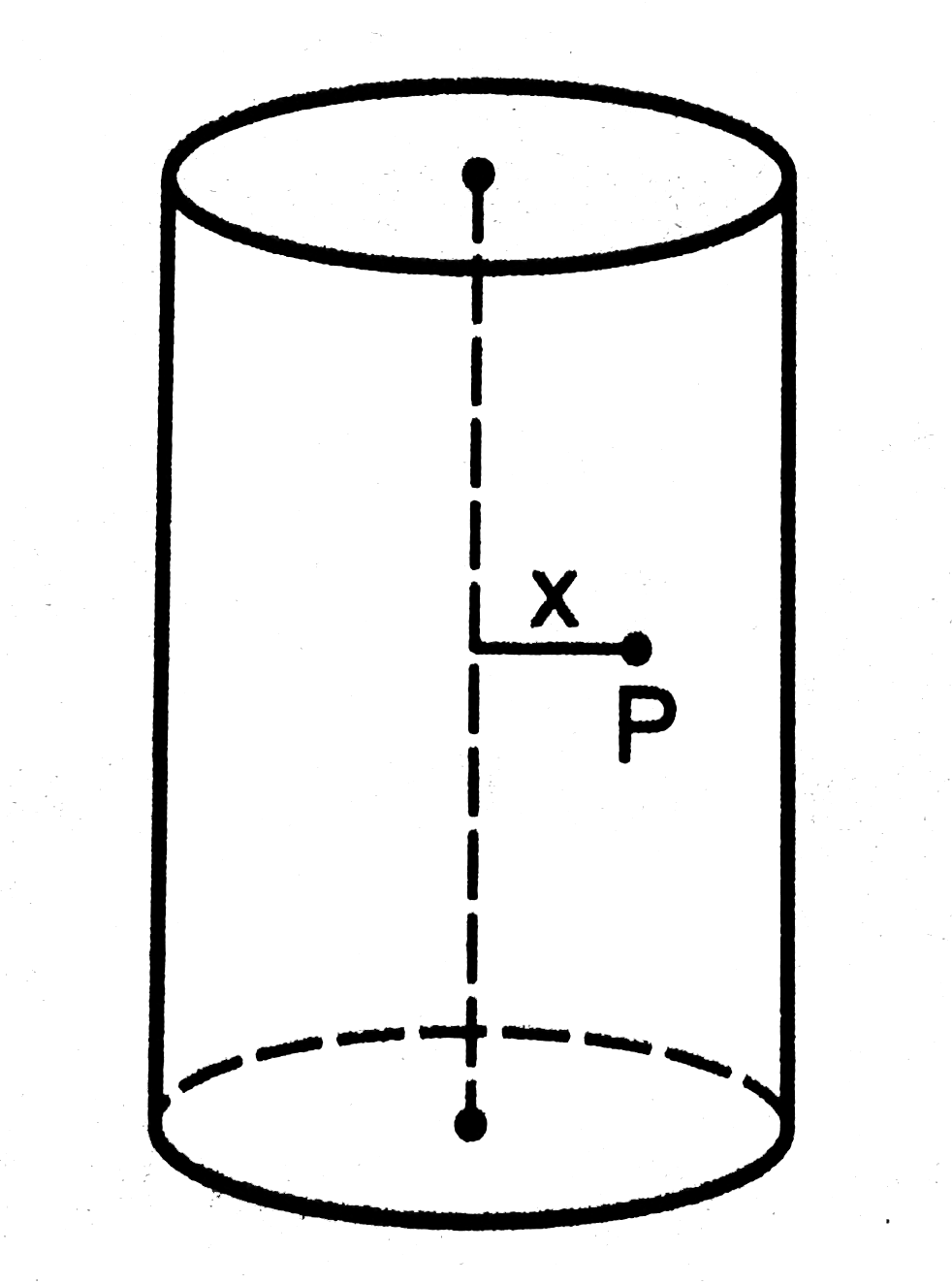
A long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane.
View SolutionA long cylindrical volume (of radius R) contains a uniformly distributed charge of density ρ. Consider a point P inside the cylindrical volume at a distance x from its axis as shown in the figure. Here x can be more than or less than R. Electric field at point P is :

View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionA long wire carries a current of 4.00 A. Find the energy stored in the magnetic field inside a volume of 1.0mm3 at a distance of 10.0 cm from the wire.
View SolutionA large conducting plane has a surface charge density 1.0x10−4Cm−2 . Find the electrostatic energy stored in a cubical volume of edge 1 cm in the front plane.
View SolutionThe electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View SolutionAn electric dipole consists of charges ±2.0×10−8C separated by a distance of 2.0×10−3 m. It is placed near a long line charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such that the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.

View SolutionA charge of (3.14×10−6) C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rad s^-1 . Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
View Solution
