Find the fluz f the electric field through a spherical surface of radius R due to a charge of 10−7C at the centre and another equal charge at a point 2R away from the centre (figure ).

Given: magnitude of the two charges
placed = (10−7)C
We know from Gauss's law that the flux
experience by the sphere is only by due
to internal charge and not by the external
one.
Now,
E×ds=(Qε0)=10−78.85×(10+12)
=1.1×(104)N−mC.
Topper's Solved these Questions
- GAUSS LAWBook:HC VERMA ENGLISHChapter:GAUSS LAWExercise:Short Question
Explore 7 Videos
- GAUSS LAWBook:HC VERMA ENGLISHChapter:GAUSS LAWExercise:Objective 2
Explore 8 Videos
- ELECTROMAGNETIC WAVESBook:HC VERMA ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Exercise
Explore 8 Videos
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Question For short Answer
Explore 18 Videos
Similar Questions
Find the flux of the electric field through a spherical surface of radius R due to a charge of 8.85×10−8C at the centre and another equal charge at a point 3R away from the centre (Given : ε0=8.85×10−12 units )
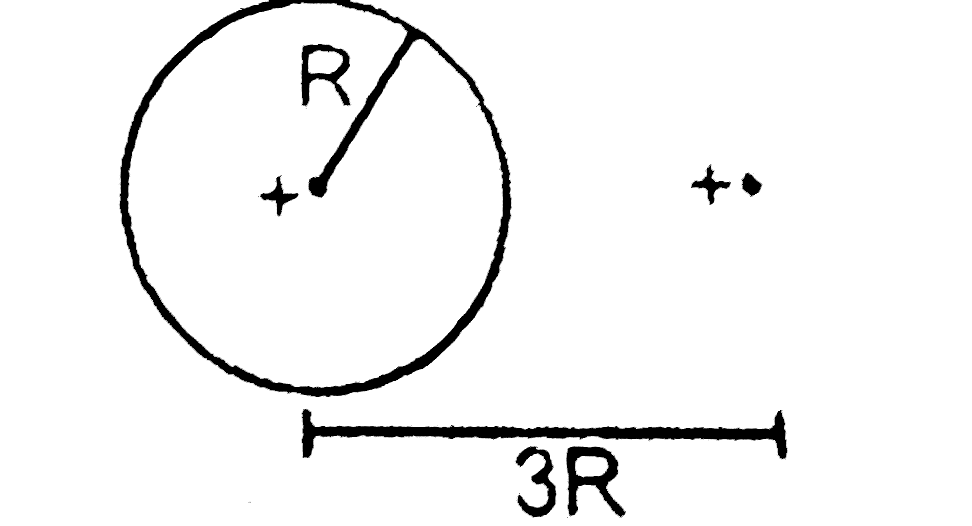
View SolutionA spherical conductor of radius 10 cm has a charge of 3.2 x 10^-7 C distributed uniformly. What is magnitude of electric field at point 15 cm from centre of sphere?
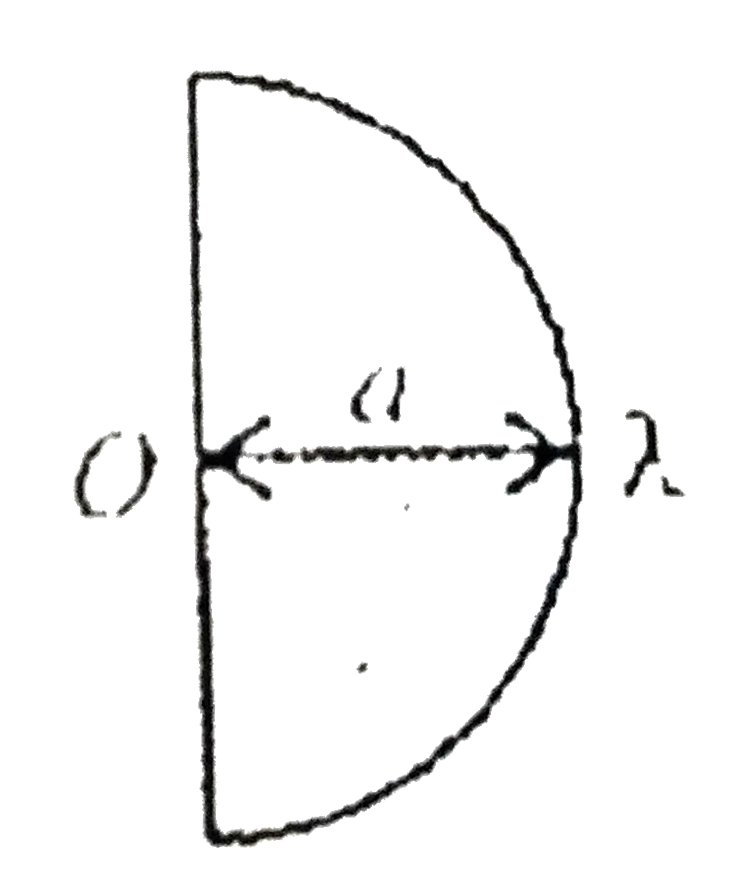
View SolutionElectric field at centre of a uniforly charged semicirlce of radius a is
View SolutionThe surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc σ2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
View SolutionA point charge Q is placed at the centre of a spherical conducting shell. A total charge of -q is placed on the shell. The magnitude of the electric field at point P1 at a distance R1 from the centre is X. The magnitude of the electric field due to induced charges at point P2 a distance R2 from the centre is Y. The values of X and Y are respectively.

View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View SolutionFind out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
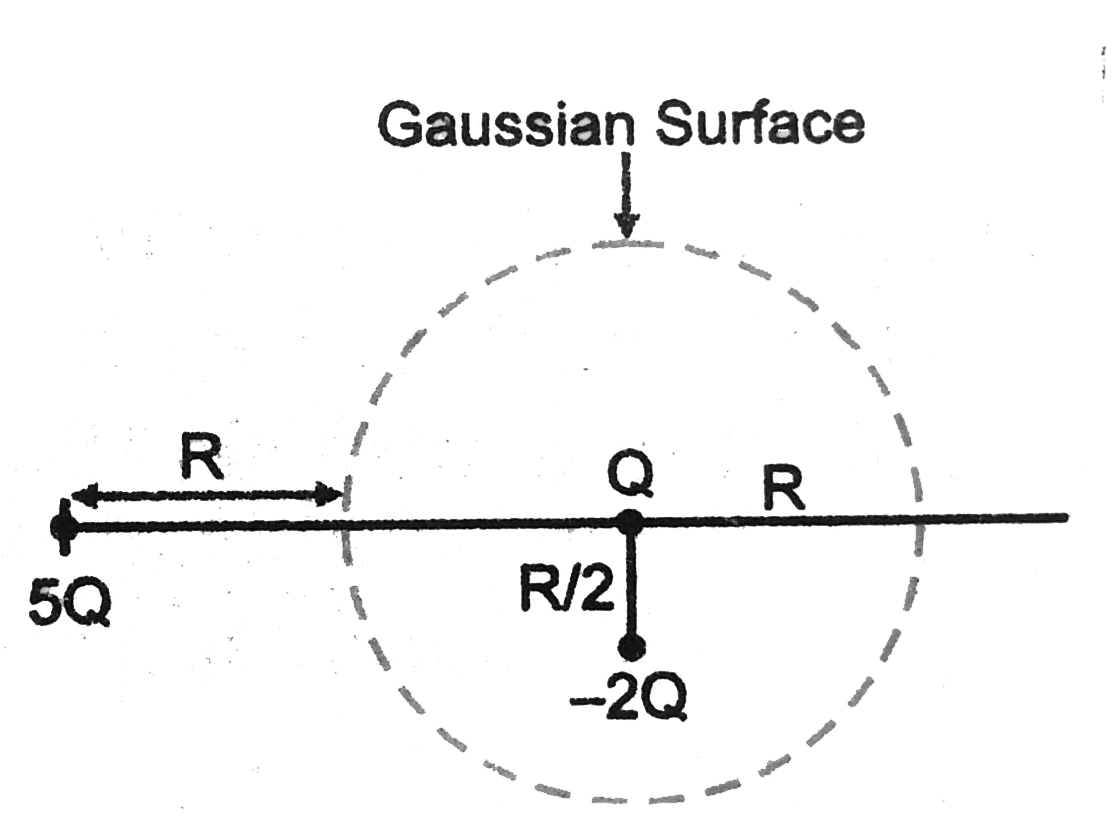
View SolutionRefer to the arrangement of charges in Fig and a Gaussian surface of radius R with Q at the centre. Then
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution

