A particle of mass m and charge −Q is constrained to move along the axis of a ring of radius a. The ring carries a uniform charge density +λ along its length. Initially, the particle is in the centre of the ring where the force on it is zero. Show that the period of oscillation of the particle when it is displaced slightly from its equilibrium position is given by
T=2πsq√2ε0ma2λQ
The correct Answer is:A
To solve the problem of finding the period of oscillation of a charged particle constrained to move along the axis of a charged ring, we will follow these steps:
Step 1: Determine the total charge on the ring
The ring has a uniform charge density λ and a radius a. The total charge Q on the ring can be calculated using the formula for the circumference of the ring:
\(
Q = \lambda \cdot (2\pi a)
\)
Step 2: Analyze the equilibrium position
Initially, the particle of mass m and charge −Q is placed at the center of the ring. At this position, the net force acting on the particle is zero due to the symmetry of the electric field produced by the ring.
Step 3: Calculate the electric field at a distance x from the center
When the particle is displaced a small distance x along the axis of the ring, we need to calculate the electric field E at that point. The electric field due to a ring of charge at a distance x along its axis is given by:
\(
E = \frac{1}{4\pi \epsilon_0} \cdot \frac{Qx}{(a^2 + x^2)^{3/2}}
\)
Substituting Q=λ⋅(2πa), we get:
\(
E = \frac{1}{4\pi \epsilon_0} \cdot \frac{(2\pi a \lambda)x}{(a^2 + x^2)^{3/2}}
\)
Step 4: Simplify the electric field for small displacements
For small displacements where \( x \ll a \), we can approximate \( (a^2 + x^2)^{3/2} \approx a^3 \). Thus, the electric field simplifies to:
\(
E \approx \frac{1}{4\pi \epsilon_0} \cdot \frac{(2\pi a \lambda)x}{a^3} = \frac{\lambda}{2\epsilon_0 a^2} x
\)
Step 5: Calculate the force acting on the particle
The force F acting on the particle due to the electric field is given by:
\(
F = -Q \cdot E = -(-Q) \cdot \left(\frac{\lambda}{2\epsilon_0 a^2} x\right) = \frac{Q \lambda}{2\epsilon_0 a^2} x
\)
Step 6: Relate the force to the restoring force
The force can be expressed in the form of Hooke's law:
\(
F = -kx
\)
where \( k = \frac{Q \lambda}{2\epsilon_0 a^2} \).
Step 7: Find the period of oscillation
The time period \( T \) of oscillation for a mass-spring system is given by:
\(
T = 2\pi \sqrt{\frac{m}{k}}
\)
Substituting the value of \( k \):
\(
T = 2\pi \sqrt{\frac{m \cdot 2\epsilon_0 a^2}{Q \lambda}}
\)
Step 8: Final expression for the period
Thus, the period of oscillation is:
\(
T = 2\pi \sqrt{\frac{2\epsilon_0 m a^2}{\lambda Q}}
\)
The ring has a uniform charge density λ and a radius a. The total charge Q on the ring can be calculated using the formula for the circumference of the ring:
\(
Q = \lambda \cdot (2\pi a)
\)
Initially, the particle of mass m and charge −Q is placed at the center of the ring. At this position, the net force acting on the particle is zero due to the symmetry of the electric field produced by the ring.
When the particle is displaced a small distance x along the axis of the ring, we need to calculate the electric field E at that point. The electric field due to a ring of charge at a distance x along its axis is given by:
\(
E = \frac{1}{4\pi \epsilon_0} \cdot \frac{Qx}{(a^2 + x^2)^{3/2}}
\)
Substituting Q=λ⋅(2πa), we get:
\(
E = \frac{1}{4\pi \epsilon_0} \cdot \frac{(2\pi a \lambda)x}{(a^2 + x^2)^{3/2}}
\)
For small displacements where \( x \ll a \), we can approximate \( (a^2 + x^2)^{3/2} \approx a^3 \). Thus, the electric field simplifies to:
\(
E \approx \frac{1}{4\pi \epsilon_0} \cdot \frac{(2\pi a \lambda)x}{a^3} = \frac{\lambda}{2\epsilon_0 a^2} x
\)
The force F acting on the particle due to the electric field is given by:
\(
F = -Q \cdot E = -(-Q) \cdot \left(\frac{\lambda}{2\epsilon_0 a^2} x\right) = \frac{Q \lambda}{2\epsilon_0 a^2} x
\)
The force can be expressed in the form of Hooke's law:
\(
F = -kx
\)
where \( k = \frac{Q \lambda}{2\epsilon_0 a^2} \).
The time period \( T \) of oscillation for a mass-spring system is given by:
\(
T = 2\pi \sqrt{\frac{m}{k}}
\)
Substituting the value of \( k \):
\(
T = 2\pi \sqrt{\frac{m \cdot 2\epsilon_0 a^2}{Q \lambda}}
\)
Thus, the period of oscillation is:
\(
T = 2\pi \sqrt{\frac{2\epsilon_0 m a^2}{\lambda Q}}
\)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Positive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View SolutionA ring of radius a contains a charge q distributed. uniformly ober its length. Find the electric field at a point. on the axis of the ring at a distance x from the centre.
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionThree equal negative charges, −q1 each form the vertices of and equilateral triangle . A particle of mass m and a positive charge q2 is constrained to move along a line perpendicular to the plane of triangle and through its center, which at a distance r from each of the negative charges as shown in fig. The whole systen is kept in gravity-free space, Find the time period of vibration of the particle for small displacement from the equilibrium position.

View SolutionA point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
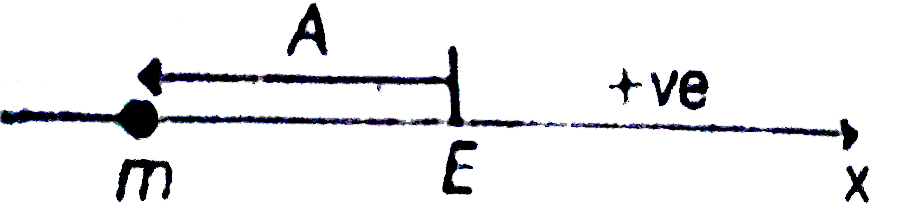
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
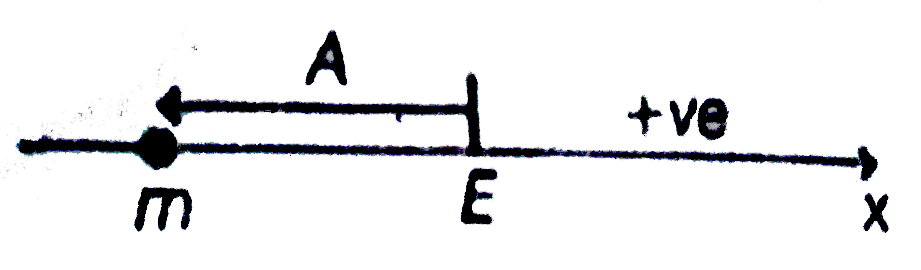
View Solution
