A smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

Let the particle displace slightly toward right at a distance
r from the centre. The force acting on the particle is
→F=−q→E,whereE=ρ3ε0→r
=−ρq3ε0→r
or m→a=−ρq3ε0→ror→a=−ρq3mε0→r
Hence, the force acting on the particle is making the particles
execute SHM. Comparing with →a=−ω2→r, we get
ω2=ρq3mε0
Hence, the time period of oscillation of the particle is
T=2π√3ε0mρq.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.116videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Exercise 2.214videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
Potential difference beween centre and surface of the sphere of radius R and uniorm volume charge density ρ within it will be
View SolutionA cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle θ=450 as shown. The electron (of mass m and charge –e) will take (P√2mrε0eaρ)1/2 time to touc the sphere again. Neglect gravity. find the value of P:
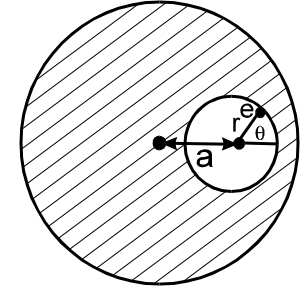 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
Flux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
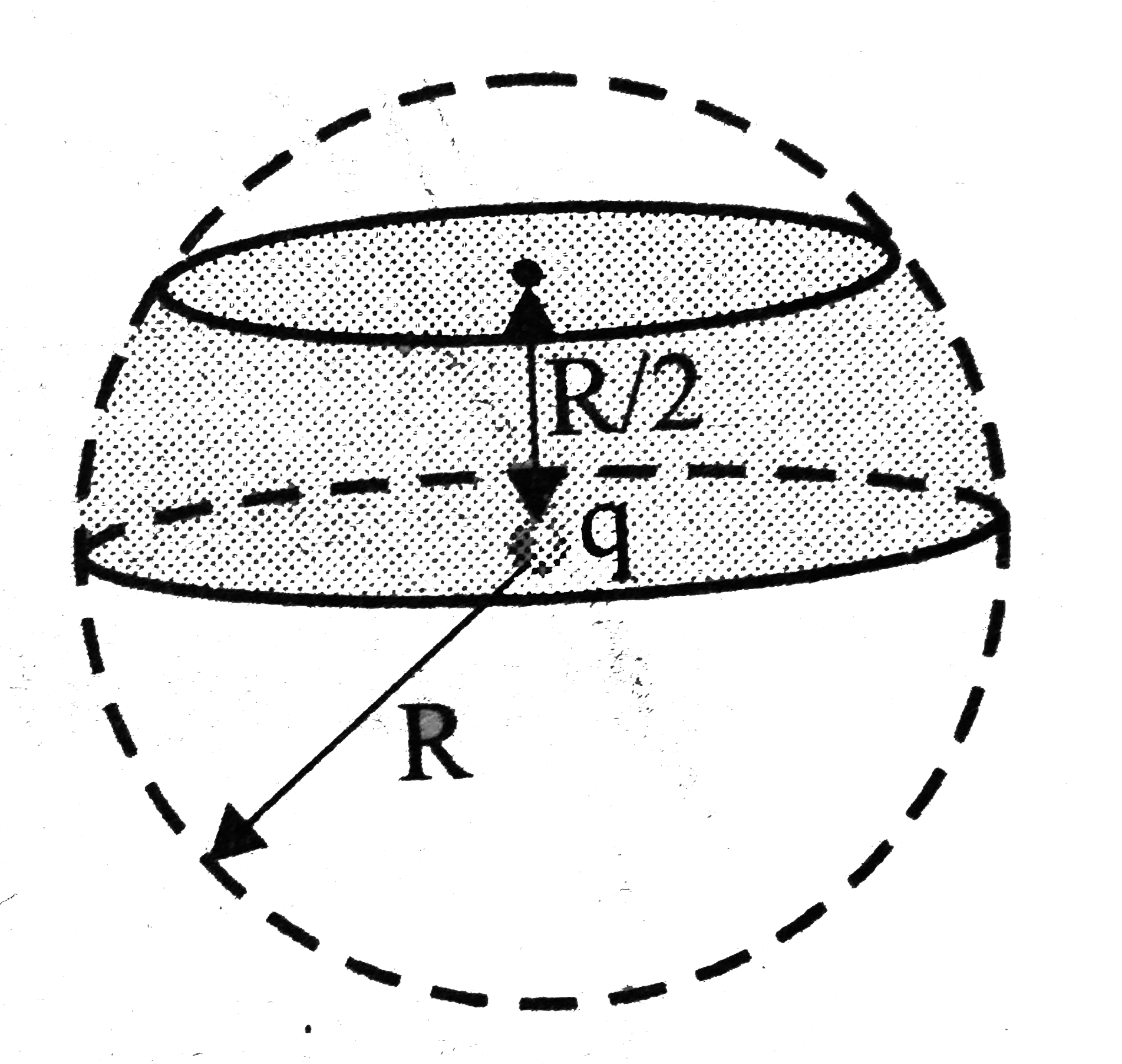 View Solution
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionA conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are
View SolutionSurface charge density of a sphere of a radius 10 cm is 8.85×10−8c/m2. Potential at the centre of the sphere is
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
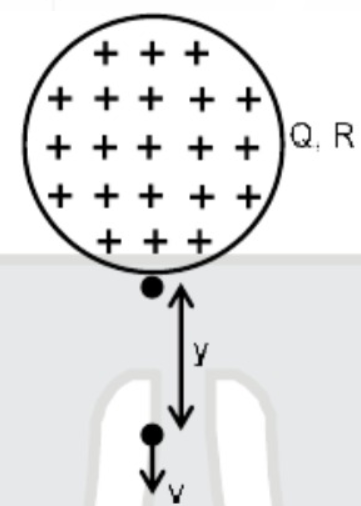 View Solution
View Solution
