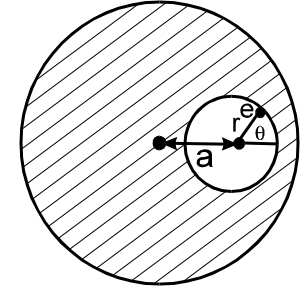
A cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle θ=450 as shown. The electron (of mass m and charge –e) will take (P√2mrε0eaρ)1/2 time to touc the sphere again. Neglect gravity. find the value of P:
The correct Answer is:B
F=eE=epa3e0
r√2=12Fmt2
t=√6√2re0mepa⎞⎟
⎟⎠

Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
A smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View Solution
Knowledge Check
The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
ARB0.5RC√0.6RD√0.3R
A solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionPotential difference beween centre and surface of the sphere of radius R and uniorm volume charge density ρ within it will be
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionThe electric potential due to uniformly charged sphere of radius R,having volume charge density rho having a spherical cavity of radius R2 as shown as in figure at point p is
_PHY_E05_288_Q01.png)
View SolutionWhat is potential at a distance r(<R) in a dielectric sphere of uniform charge density ρ, radius R and dielectric constant εr.
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View Solution
