An electric field given by pierces a Gussian cube of side 1 m placed at origin such that its three sides represents x,y and z axes. The net charge enclosed within the cube is , where is _____. (take )
The correct Answer is:A
To solve the problem, we need to find the net charge enclosed within a Gaussian cube placed at the origin in an electric field given by →E=4^i−(20y2+2)^j.
1. Identify the Electric Field Components:
The electric field is given as:
→E=4^i−(20y2+2)^j
Here, the x-component of the electric field is constant (Ex=4), and the y-component varies with y (Ey=−(20y2+2)).
2. Determine the Area Vectors for the Cube:
The cube has six faces, and we need to consider the area vectors for each face:
- For the face at y=0 (downward): ^A=−^j
- For the face at y=1 (upward): ^A=^j
- The faces at x=0 and x=1 will have area vectors in the ^i direction.
- The faces at z=0 and z=1 will have area vectors in the ^k direction.
3. Calculate the Electric Flux through Each Face:
- For the face at y=0:
Ey=−(20(0)2+2)=−2(downward)
Φy=0=E⋅A=(−2)(1⋅1)=−2Wb
- For the face at y=1:
Ey=−(20(1)2+2)=−22(upward)
Φy=1=E⋅A=(−22)(1⋅1)=−22Wb
- For the faces at x=0 and x=1:
The electric field in the ^i direction does not contribute to the net flux since the area vectors are perpendicular to the electric field.
Φx=0=0,Φx=1=0
- For the faces at z=0 and z=1:
Similarly, the electric field has no component in the ^k direction, so:
Φz=0=0,Φz=1=0
4. Calculate the Total Electric Flux:
The total electric flux through the cube is:
Φtotal=Φy=0+Φy=1+Φx=0+Φx=1+Φz=0+Φz=1=−2−22+0+0+0+0=−24Wb
5. Use Gauss's Law to Find the Enclosed Charge:
According to Gauss's law:
Φ=Qenclosedϵ0
Rearranging gives:
Qenclosed=Φ⋅ϵ0
Substituting the values:
Qenclosed=−24×(8.85×10−12)=−2.124×10−10C
6. Express the Charge in the Required Form:
The problem states that the net charge enclosed is x×10−10C. Thus:
x=−2.124
Final Answer:
The value of x is approximately −2.124.
The electric field is given as:
→E=4^i−(20y2+2)^j
Here, the x-component of the electric field is constant (Ex=4), and the y-component varies with y (Ey=−(20y2+2)).
The cube has six faces, and we need to consider the area vectors for each face:
- For the face at y=0 (downward): ^A=−^j
- For the face at y=1 (upward): ^A=^j
- The faces at x=0 and x=1 will have area vectors in the ^i direction.
- The faces at z=0 and z=1 will have area vectors in the ^k direction.
- For the face at y=0:
Ey=−(20(0)2+2)=−2(downward)
Φy=0=E⋅A=(−2)(1⋅1)=−2Wb
- For the face at y=1:
Ey=−(20(1)2+2)=−22(upward)
Φy=1=E⋅A=(−22)(1⋅1)=−22Wb
- For the faces at x=0 and x=1:
The electric field in the ^i direction does not contribute to the net flux since the area vectors are perpendicular to the electric field.
Φx=0=0,Φx=1=0
- For the faces at z=0 and z=1:
Similarly, the electric field has no component in the ^k direction, so:
Φz=0=0,Φz=1=0
The total electric flux through the cube is:
Φtotal=Φy=0+Φy=1+Φx=0+Φx=1+Φz=0+Φz=1=−2−22+0+0+0+0=−24Wb
According to Gauss's law:
Φ=Qenclosedϵ0
Rearranging gives:
Qenclosed=Φ⋅ϵ0
Substituting the values:
Qenclosed=−24×(8.85×10−12)=−2.124×10−10C
The problem states that the net charge enclosed is x×10−10C. Thus:
x=−2.124
The value of x is approximately −2.124.
Topper's Solved these Questions
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:LEVEL - 2
Explore 60 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE MAIN
Explore 65 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:LEVEL - 0 (LONG ANSWER TYPE )
Explore 8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:IMPECCABLE
Explore 52 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
Similar Questions
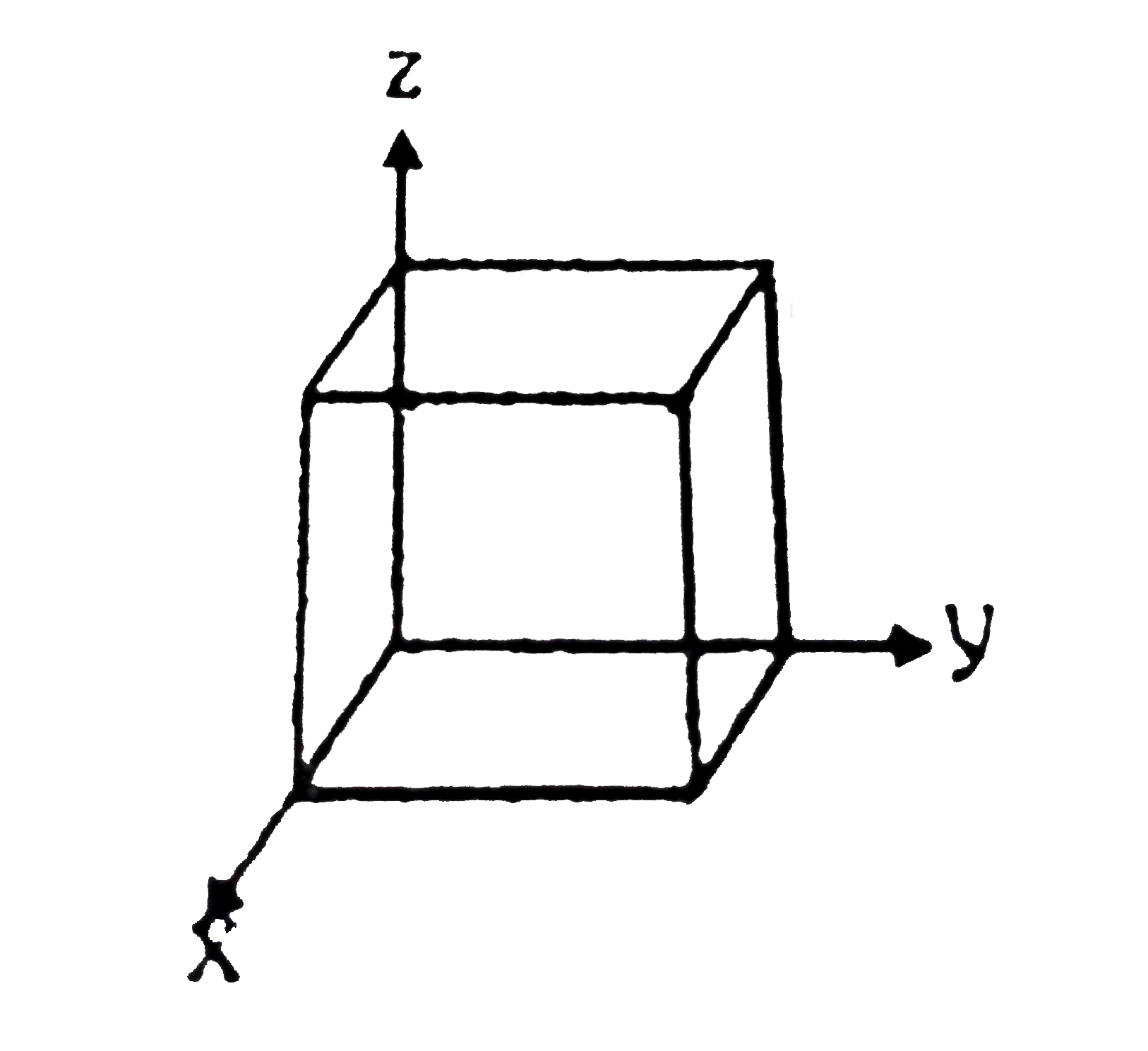
Electric field in a region is given by →E=−4xˆi+6yˆj. Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram
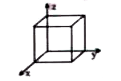
View SolutionElectric field in a region is given by →E=−4xˆi+6yˆj. The charge enclosed in the cube of side 1m oriented as shown in the diagram is given by α∈0. Find the value of α.
View SolutionAn electric dipole of moment rp=(ˆi+2ˆj)×10−28Cm is at origin. The electric field at point ( 2,4) due to the dipole is parallelto
View SolutionAn electric dipole of moment rp=(ˆi+2ˆj)×10−28Cm is at origin. The electric field at point ( 2,4) due to the dipole is parallelto
View SolutionThe electric field in a region of space is given by, →E=E0ˆi+2E0ˆj where E0=100N/C. The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly.
View SolutionAn electric dipole moment →P=(2.0ˆI+3.0ˆj)μCm is placed in a uniform electric field
→E=(3ˆI+2.0ˆk)×105NC−1.
View SolutionAn electric field is given by →E=(yˆi+xˆj)NC. Find the work done (in J) in moving a 1C charge from →rA=(2ˆi+2ˆj) m to →rB=(4ˆi+ˆj)m.
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionIn Region of Electric field Given by →E=(Ax−B)ˆI. Where A=20 unit and B=10 unit. If Electric potential at x=1m is v1 and at x=−5m is v2. Then v1−v2 is equal to
View SolutionA cube has a side length 1.2×10−2m.Calculate its volume
View Solution