The electric potential V is given as a function of distance x (metre) by V=(6x2+10x−9) volt. Find magnitude of electric field (in V/m) at x= 4.
To find the magnitude of the electric field at x=4 for the given electric potential function V=6x2+10x−9, we will follow these steps:
Step 1: Differentiate the Electric Potential Function
The electric field E is related to the electric potential V by the equation:
E=−dVdx
First, we need to differentiate the given potential function V with respect to x.
Given:
V=6x2+10x−9
Differentiating V:
dVdx=ddx(6x2)+ddx(10x)+ddx(−9)
Using the power rule for differentiation:
dVdx=12x+10+0=12x+10
Step 2: Calculate the Electric Field
Now, we can find the electric field E by substituting the derivative we just calculated into the equation for E:
E=−dVdx=−(12x+10)
Step 3: Substitute x=4 into the Electric Field Equation
Now, we will substitute x=4 into the expression for the electric field:
E=−(12(4)+10)
Calculating this:
E=−(48+10)=−58V/m
Step 4: Find the Magnitude of the Electric Field
The magnitude of the electric field is the absolute value of E:
|E|=58V/m
Final Answer
The magnitude of the electric field at x=4 is 58V/m.
---
The electric field E is related to the electric potential V by the equation:
E=−dVdx
First, we need to differentiate the given potential function V with respect to x.
V=6x2+10x−9
dVdx=ddx(6x2)+ddx(10x)+ddx(−9)
Using the power rule for differentiation:
dVdx=12x+10+0=12x+10
Now, we can find the electric field E by substituting the derivative we just calculated into the equation for E:
E=−dVdx=−(12x+10)
Now, we will substitute x=4 into the expression for the electric field:
E=−(12(4)+10)
Calculating this:
E=−(48+10)=−58V/m
The magnitude of the electric field is the absolute value of E:
|E|=58V/m
The magnitude of the electric field at x=4 is 58V/m.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
Similar Questions
The electric potential V is givne as a function of distance x (metre) by V=(5x2+10x−9) volt. Value of electric field at x=1is
View SolutionThe electric potential V is givne as a function of distance x (metre) by V=(5x2+10x−9) volt. Value of electric field at x=1is
View SolutionThe variation of potential with distance x from a fixed point is shown in figure. Find the magnitude of the electric field (in V/m) at x=13m.

View SolutionThe electrostatic potential V at any point (x, y, z) in space is given by V=4x2
View SolutionIf the potential function is define as V=(−3x+4y+12z)V, then magnitude of electric field E(x,y,z) is
View SolutionElectric potential V in space as a function of cartesian co-ordinates is given by V=1x+1y+1z. Then find electric field intensity at (1, 1, 1)
View SolutionThe figure gives the electric potential V as a function of distance through five regions on x-axis. Which of the following is true for the electric E in these regions ?
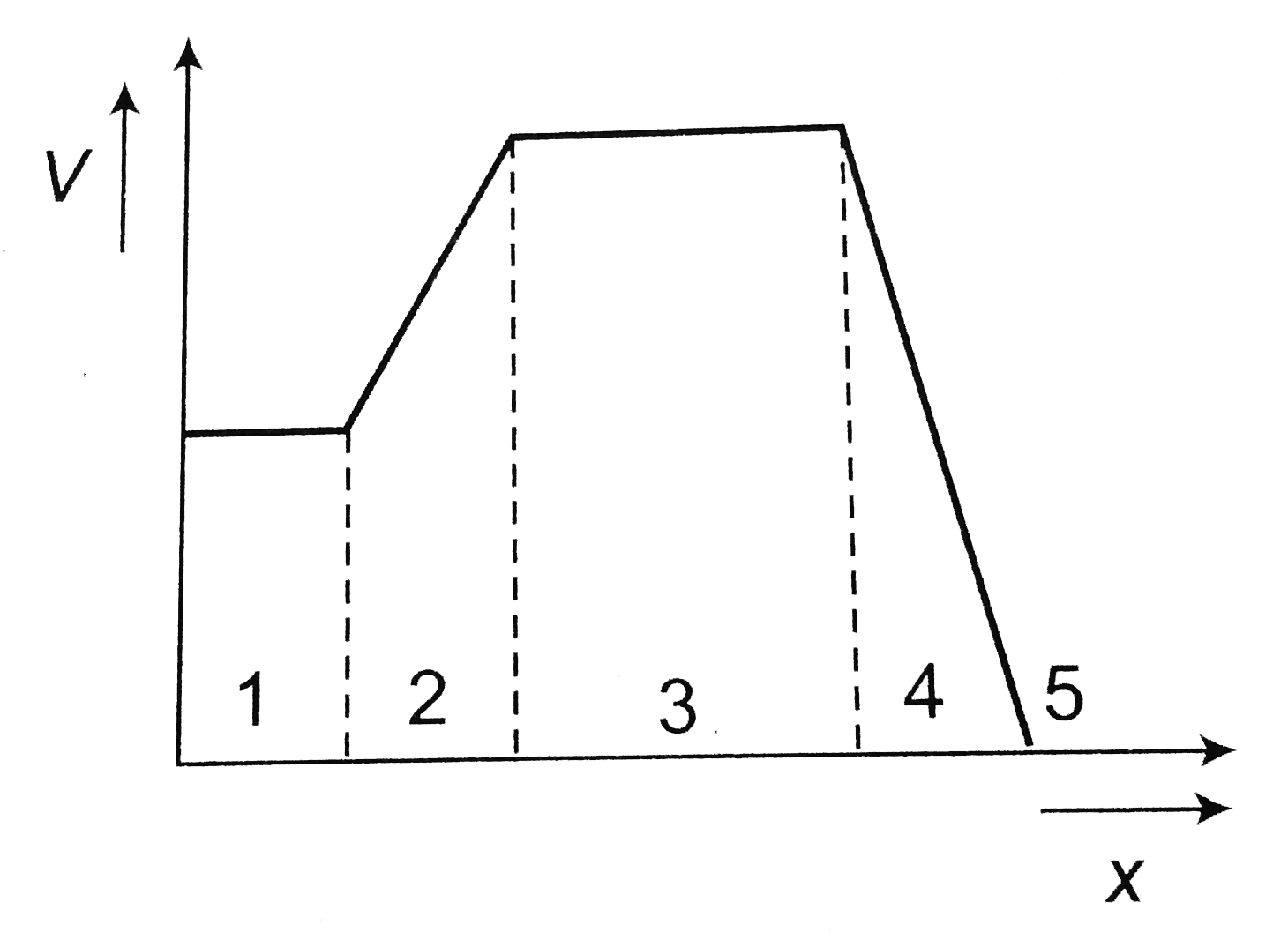
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by V=4x2 volt. The electric field at the point (1m,0,2m) is ……………Vm.
View SolutionThe electric potential V at any point (x,y,z), all in meters in space is given by V=4x2 volt. The electric field at the point (1,0,2) in volt//meter is
View SolutionIf on the x - axis electric potential decreases uniform from 60 V to 20 V between x = -2 m to x = +2 m then the magnitude of electric field at the origin
View Solution
