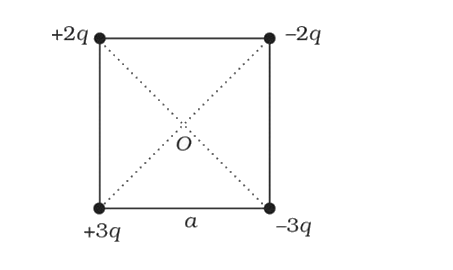
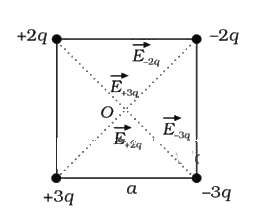
Four charge +2q,−2q,−3q and +3q are kept in the comers of a square of side . The total field at the centre of k(nqa2, find n.(K=14πε0,take√2=1.414).
The correct Answer is:A, D
→E=→E+2q+→E−3q+→E+3q
E=√2(E+3q+E−2q)
e=√25q4πe0(a√2)2,E=10√2q4πe0a2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )
8 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
Similar Questions
Four charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the souare will be (where k = 14πε0 )
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionFour equal charges are kept fixed on the vertices of a square of side 'a'. A charge q1 is kept at the centre of the square as shown in the figure . Then
View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View SolutionFour electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is

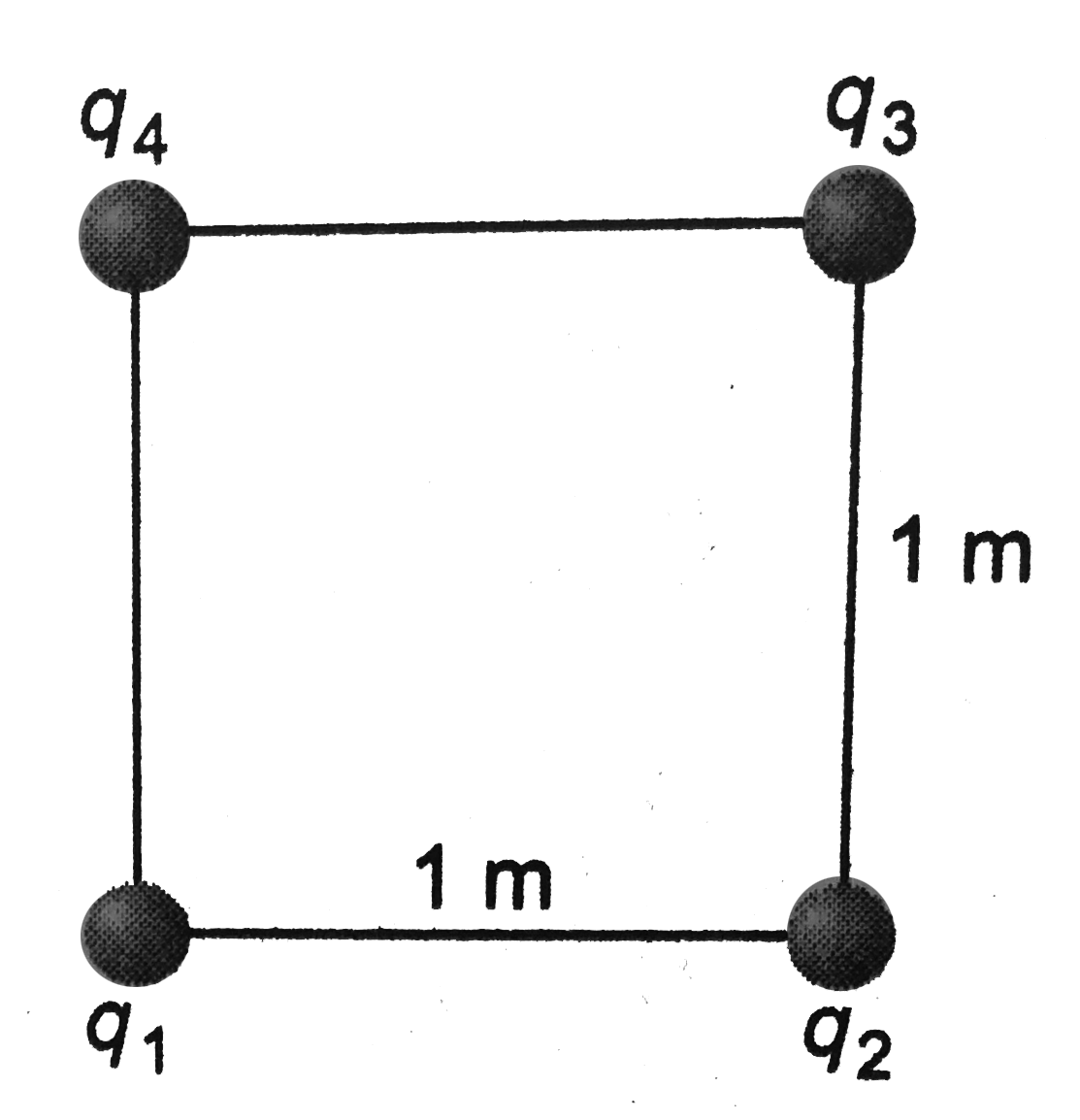
View SolutionFor charges q1=1μC,q2=2μC,q3=−3μC and q4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
View SolutionIf charges q/2 and 2q are placed at the centre of face and at the corner of a cube, then the total flux through the cube will be
View SolutionFour point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
View SolutionFour point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
View Solution
