A solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
q3 is
Q(a+b)a−b
Qa2b
Q(a−b)b
−Qba
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving a solid metallic sphere and a conducting spherical shell, and how the charges and potentials change throughout the process.
1. Initial Setup:
- We have a solid metallic sphere of radius a with charge Q.
- Surrounding it is a conducting spherical shell of radius b (where b>a).
- The potential at the surface of the solid sphere is V and at the surface of the spherical shell is Vb.
2. Charge on the Shell:
- The student puts a charge of −4Q on the conducting shell.
- The total charge on the shell is now −4Q.
3. Potential Difference:
- The potential difference between the solid sphere and the shell is measured as ΔV=V−Vb.
4. Earthing the Shell:
- The outer shell is connected to the earth. When this happens, the potential of the shell becomes zero, and the charge on the shell redistributes.
- The charge on the outer shell becomes 0 (since it is earthed).
5. Charge Redistribution:
- Since the shell is earthed, it will have no net charge. The charge −4Q will flow to the earth, leaving the shell with 0 charge.
- The charge on the inner solid sphere remains Q.
6. Earthing the Inner Sphere:
- The student then decides to earth the inner solid sphere. When the solid sphere is earthed, it will also have a potential of 0.
- The charge on the inner sphere will also become 0 as it loses its charge to the earth.
7. Connecting the Two:
- After earthing both the shell and the sphere, the student connects the two with a conducting wire.
- When the two conductors are connected, they will share charge until they reach the same potential.
8. Final Charge Distribution:
- The total charge in the system before connecting the two is Q+(−4Q)=−3Q.
- When the two conductors are connected, they will form a single conducting body, and the total charge −3Q will distribute over the outer surface of the shell.
9. Charge on the Outer Shell:
- Since the shell is the outer conductor, all the charge will reside on its outer surface.
- Therefore, the charge on the outer shell after the connection is q3=−3Q.
Final Answer:
The charge on the outer shell after connecting the inner sphere and the outer shell is:
q3=−3Q
- We have a solid metallic sphere of radius a with charge Q.
- Surrounding it is a conducting spherical shell of radius b (where b>a).
- The potential at the surface of the solid sphere is V and at the surface of the spherical shell is Vb.
- The student puts a charge of −4Q on the conducting shell.
- The total charge on the shell is now −4Q.
- The potential difference between the solid sphere and the shell is measured as ΔV=V−Vb.
- The outer shell is connected to the earth. When this happens, the potential of the shell becomes zero, and the charge on the shell redistributes.
- The charge on the outer shell becomes 0 (since it is earthed).
- Since the shell is earthed, it will have no net charge. The charge −4Q will flow to the earth, leaving the shell with 0 charge.
- The charge on the inner solid sphere remains Q.
- The student then decides to earth the inner solid sphere. When the solid sphere is earthed, it will also have a potential of 0.
- The charge on the inner sphere will also become 0 as it loses its charge to the earth.
- After earthing both the shell and the sphere, the student connects the two with a conducting wire.
- When the two conductors are connected, they will share charge until they reach the same potential.
- The total charge in the system before connecting the two is Q+(−4Q)=−3Q.
- When the two conductors are connected, they will form a single conducting body, and the total charge −3Q will distribute over the outer surface of the shell.
- Since the shell is the outer conductor, all the charge will reside on its outer surface.
- Therefore, the charge on the outer shell after the connection is q3=−3Q.
The charge on the outer shell after connecting the inner sphere and the outer shell is:
q3=−3Q
Topper's Solved these Questions
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Exercise 24.1
Explore 4 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Exercise 24.2
Explore 9 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Example Type 8
Explore 3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:All Questions
Explore 135 Videos
Similar Questions
A solid metallic sphere of radius a is surrounded by a conducting spherical shell of radius b(b>a). The solid sphere is given a charge Q. A student measures the potential at the surface of the solid sphere as V and the potential at the surface of spherical shell as Vb. After taking these readings, he decides . to put charge of −4Q on the shell. He then noted the readings of the potential of solid sphere and the shell and found that the potential difference is △V .
He then connected the outer spherical shell to the earth by a conducting wire and found that the charge on the outer surface of the shell as He then decides to remove the earthing connection from the shell and earthed the inner solid sphere. Connecting the inner sphere with the earth he observes the charge on the solid sphere as q2. He then wanted to check what happens if the two are connected by the conducting wire. So he removed the earthing connection and connected a conducting wire between the solid sphere and the spherical shelll. After the connections were made he found the charge on the outer shell as q3.
Potential difference (△CV) measured by the student between the inner solid shere and outer shell after putting a charge −4Q is
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
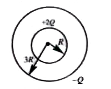
What would be the final distribution of charges if the sphres are joined by a conducting wire
View SolutionA hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere?
View SolutionA hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere?
View SolutionA uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionA uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
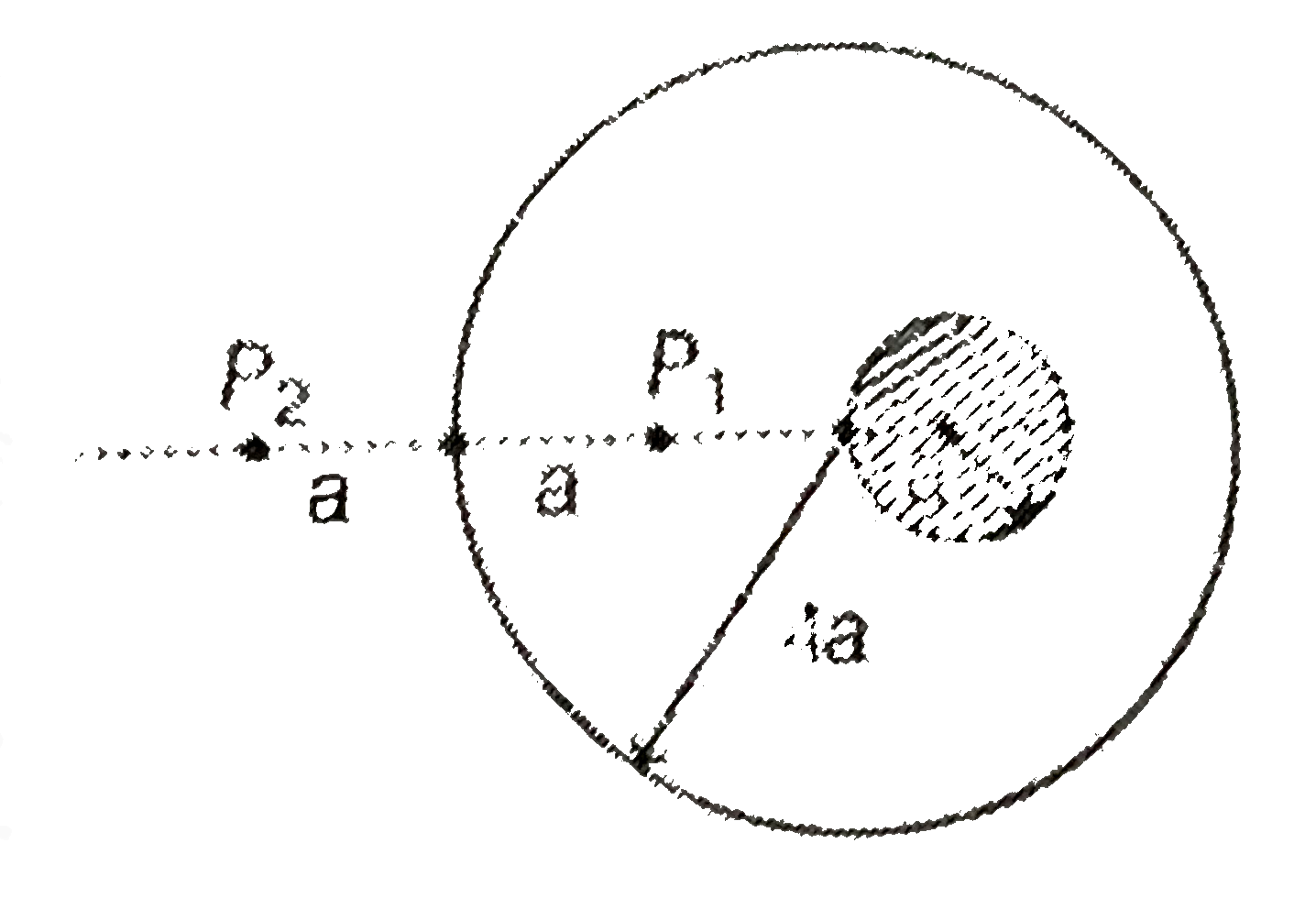
View SolutionA hollow metal sphere of radius 6 cm is charged such that the potential on its surface is 12 V.What is the potential at the centre of the sphere?
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
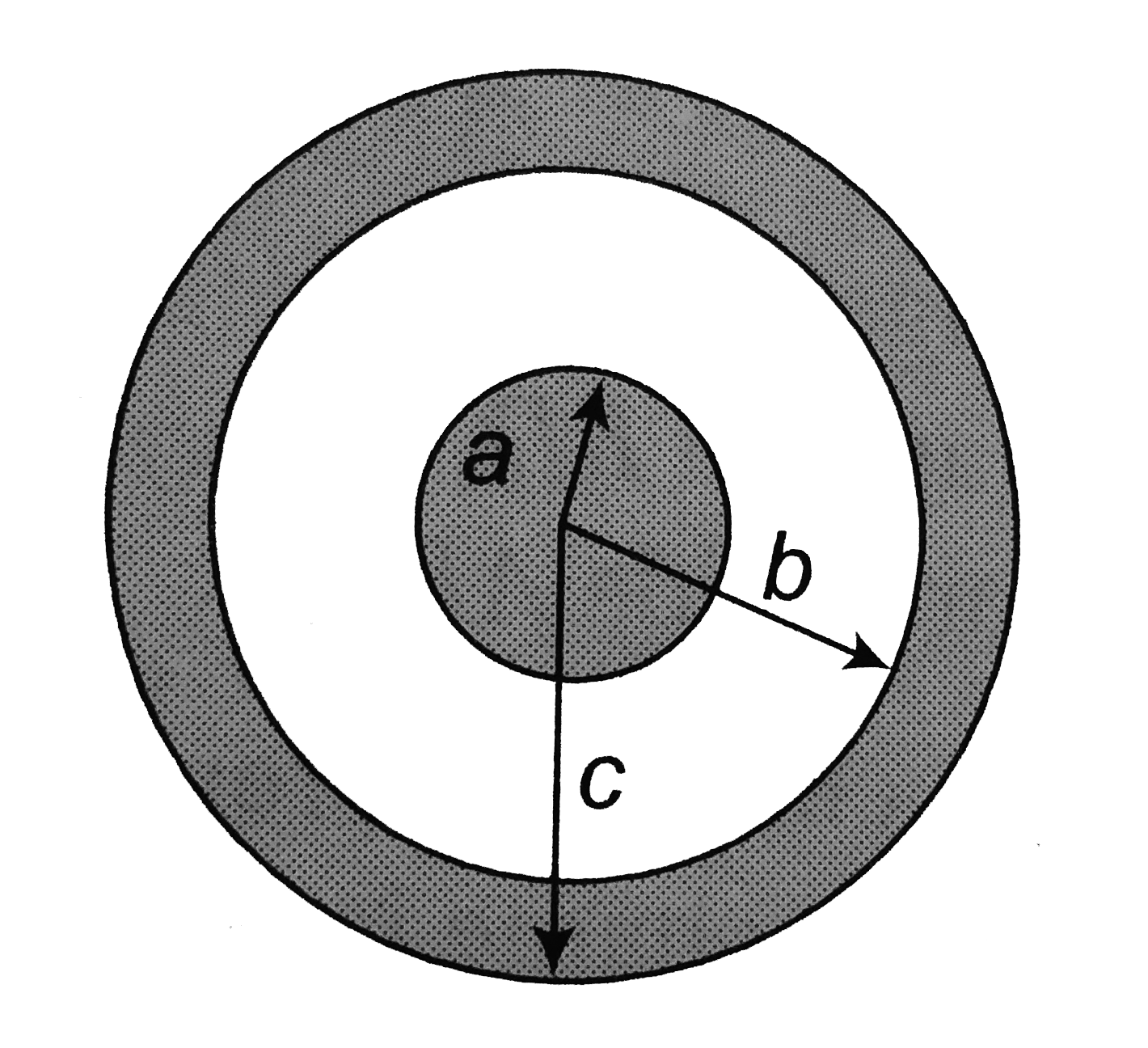
View SolutionA solid conducting sphere of radius a has a net positive charge 2Q. A conducting spherical shell of inner radius b and outer radius c is concentric with the solid sphere and has a net charge −Q. The surface charge density on the inner and outer surfaces of the spherical shell will be
View SolutionA metal sphere of radius 'a' is having charge +Q. Now it is connected by a conducting wire concentric spherical shell of radius '2a'. Then the potential at the surface of outer shell is

Here, K=14πε0
View Solution

