A conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?
The correct Answer is:B
Capacities of conducting spheres are in the ratio of their radii. Let C1 and C2 be the capacities of S1 and S2 ten
C2C1=Rr
a. Charges are disturbed in the ratio of their capacities. Let in the first contact, charge acquired by S2 is q1. Therefore, charge on S1 will be Q−q1. Say it is q1
∴q1q2=q1Q−q1=C2C1=Rr
It implies that Q charge is to be distributed in S2 and S1 in the ratio of R/r.
∴q1=Q(RR+r)......i
In the second contact S1 again acquires the same charge Q.
Therefore, total charge in S1 and S2 will be Q+q1=Q(1+RR+r)
this charge is again distributed in the same ratio. Therefore, charge on S2 in second contact.
q2=Q(1+RR+2)(RR+r)
=Q[RR+r+(RR+r)2]
Similarly, q3==Q[RR+r+(RR+r)2+(RR+r)3]
and
qn=Q[RR+r+(R(R+r)2+...+(RR+r)n]
or qn=QRr[1−(RR+r)n] ........ii
[Sn=a(1−rn)(1−r)]
Therefore, electrostatic energy of S2 after n such contacts
Un=a2n2C=(Qn)2R+r[1+RR+r+...+...+(R(R+r)n−1]
as n→∞
q∞=QRR+r⎛⎜⎝11−RR+r⎞⎟⎠
=QRR+r(R+rr)=QRr[S∞=a1−r]
∴U∞=q2∞2C=Q2R2/r28πε0R
or U∞=Q2R8πε0r2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.2
9 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 8
3 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Match the refining methods (Column I) with (Column II).
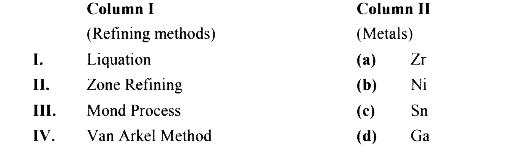
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionSelf energy of conducting sphere of radius .r. carrying charge .Q. is ______
View SolutionA sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ratio of electric flux through S1andS2,
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :
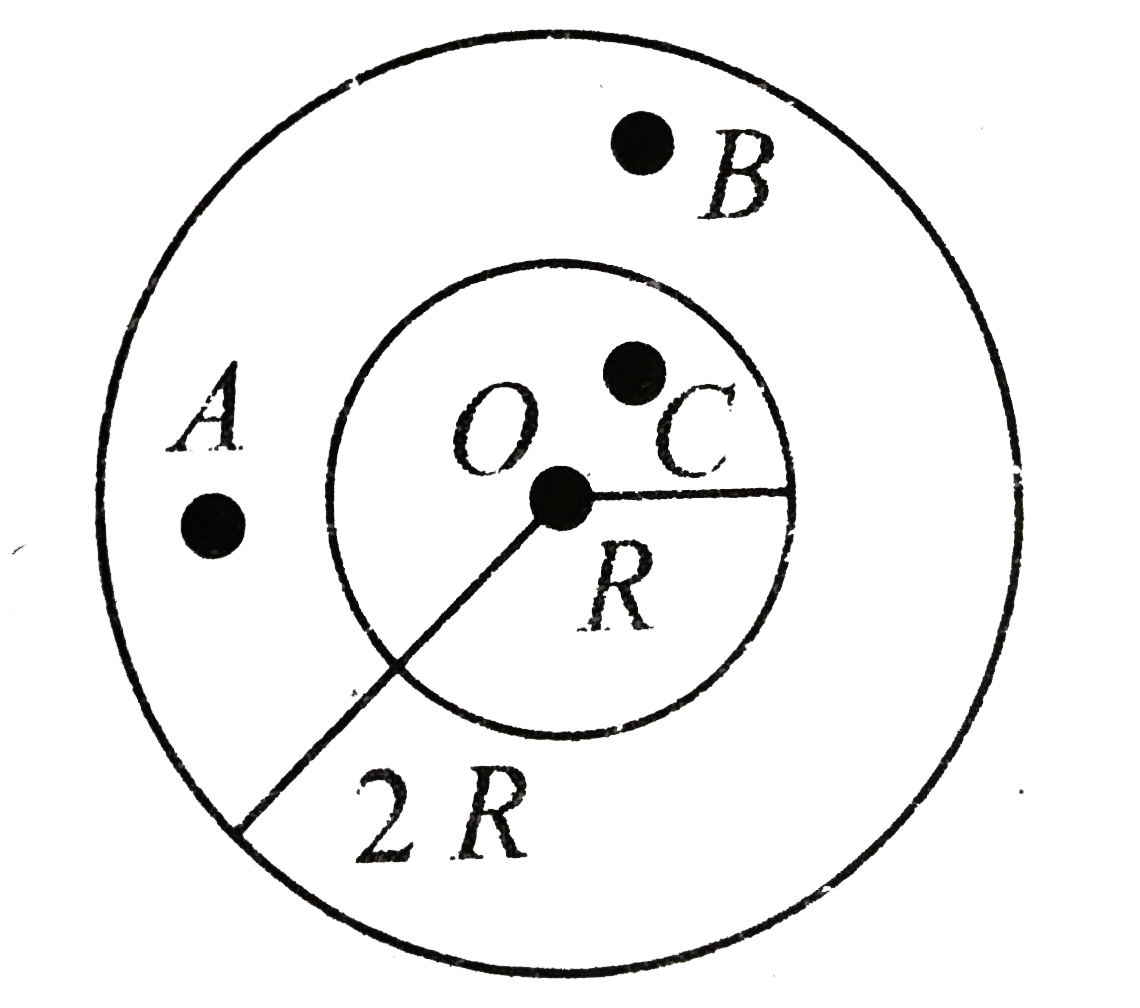
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
View SolutionA solid insulating sphere of radius R is given a charge Q. If at a point inside the sphere the potential is 1.5 times the potential at the surface, this point will be
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionTwo metal spheres, one fo radius R and the other of radius 2R, both have same surface charge density s. They are brought in contact and seprated. What will be new surface charge densitites on them ?
View Solution
