A sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ratio of electric flux through S1andS2,
To solve the problem, we need to find the ratio of electric flux through two concentric spheres, S1 and S2, where S1 encloses a charge Q and S2 is larger than S1 with no additional charges in between.
1. Understanding Electric Flux:
Electric flux (Φ) through a closed surface is given by Gauss's law, which states:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
2. Calculating Electric Flux through Sphere S1:
- Sphere S1 encloses the charge Q.
- Therefore, the electric flux through S1 is:
Φ1=Qϵ0
3. Calculating Electric Flux through Sphere S2:
- Sphere S2 is concentric with S1 and also encloses the same charge Q since there are no additional charges between S1 and S2.
- Thus, the electric flux through S2 is:
Φ2=Qϵ0
4. Finding the Ratio of Electric Fluxes:
- Now, we need to find the ratio of the electric flux through S1 and S2:
Φ1Φ2=Qϵ0Qϵ0=1
5. Conclusion:
- The ratio of electric flux through S1 and S2 is:
Φ1Φ2=1
Final Answer:
The ratio of electric flux through spheres S1 and S2 is 1:1.
Electric flux (Φ) through a closed surface is given by Gauss's law, which states:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
- Sphere S1 encloses the charge Q.
- Therefore, the electric flux through S1 is:
Φ1=Qϵ0
- Sphere S2 is concentric with S1 and also encloses the same charge Q since there are no additional charges between S1 and S2.
- Thus, the electric flux through S2 is:
Φ2=Qϵ0
- Now, we need to find the ratio of the electric flux through S1 and S2:
Φ1Φ2=Qϵ0Qϵ0=1
- The ratio of electric flux through S1 and S2 is:
Φ1Φ2=1
The ratio of electric flux through spheres S1 and S2 is 1:1.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET II
8 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET III
7 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - B
7 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A sphere of radius r, encloses a net charge Q. If there is another concentric sphere S2 of radius r2(r2>r1) enclosing charge 20, find the ratio of the electric flux through S1 and S2. How will the electric flux through sphere S1 change, if a medium of dielectric constant k is introduced in the space inside S2 in place of air?
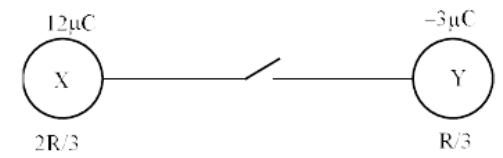
View SolutionFind ratio of charges S1 and S2 of they are connected by wire.
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionS1andS2 are two hollow concentric spheres enclosing charge Q and 2Q, respectively, as shown in figure. What is the ratio of the electric flux leaving through the surface of S1andS2?

View SolutionS1,S2,S3 are three concentric spherical shells, as shown in figure. S1 and S2 have charge 4Q and 8Q respectively, whereas S3 is uncharged. Find the ratio of the flux passing through S1 to that through S3
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View SolutionA conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?
View SolutionTwo metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
View Solution
