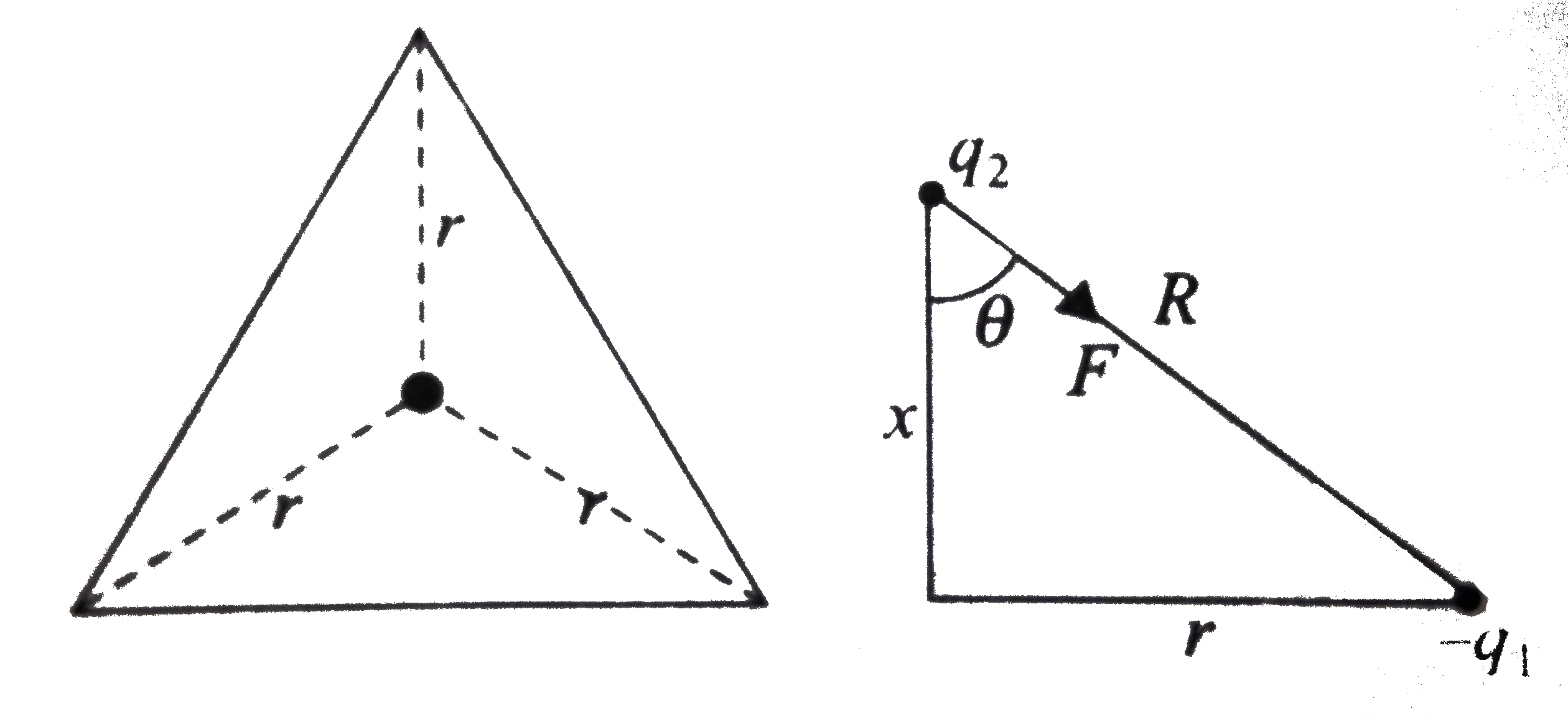
Three equal negative charges, −q1 each form the vertices of and equilateral triangle . A particle of mass m and a positive charge q2 is constrained to move along a line perpendicular to the plane of triangle and through its center, which at a distance r from each of the negative charges as shown in fig. The whole systen is kept in gravity-free space, Find the time period of vibration of the particle for small displacement from the equilibrium position.

The correct Answer is:2π√4πε0mr33q1q2
(Fnet)=3Fcosθ=3kq1q2R2xR=ma
or, a=[3kq1q24πε0mr3]x (as for small x, R=r)
T=2π√4πε0mr33kq1q2
 ,
,
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct47videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct8videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type15videos
COULOMB LAW AND ELECTRIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
Similar Questions
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View SolutionConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionThree poistive charges of equal value q are placed at the vertices of an equilateral triangle. The resulting lines of force should be sketched as in
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x is very less than R, find the time period of oscillation of the particle if it is released from there.
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
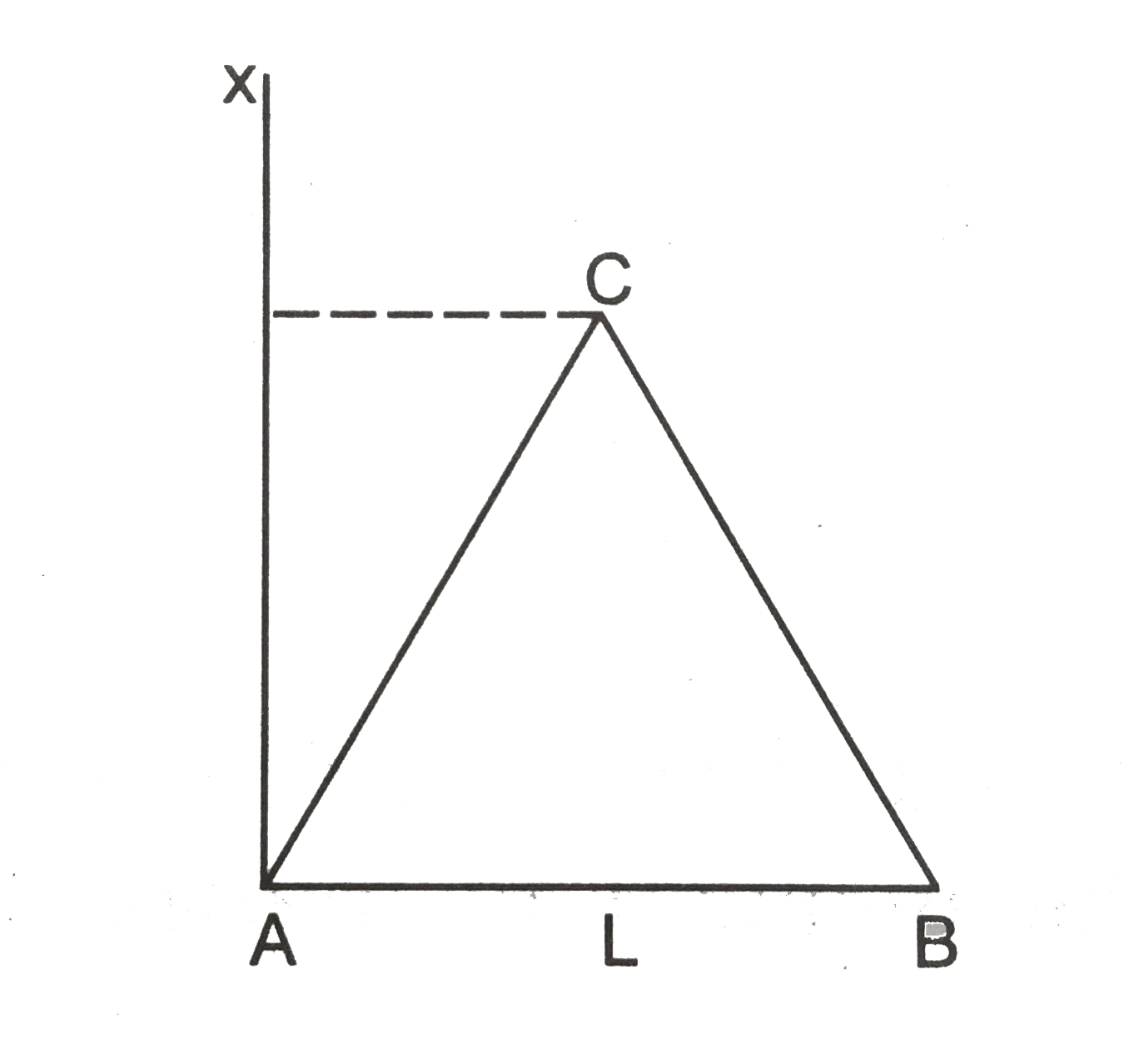
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC
 View Solution
View SolutionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View Solution


