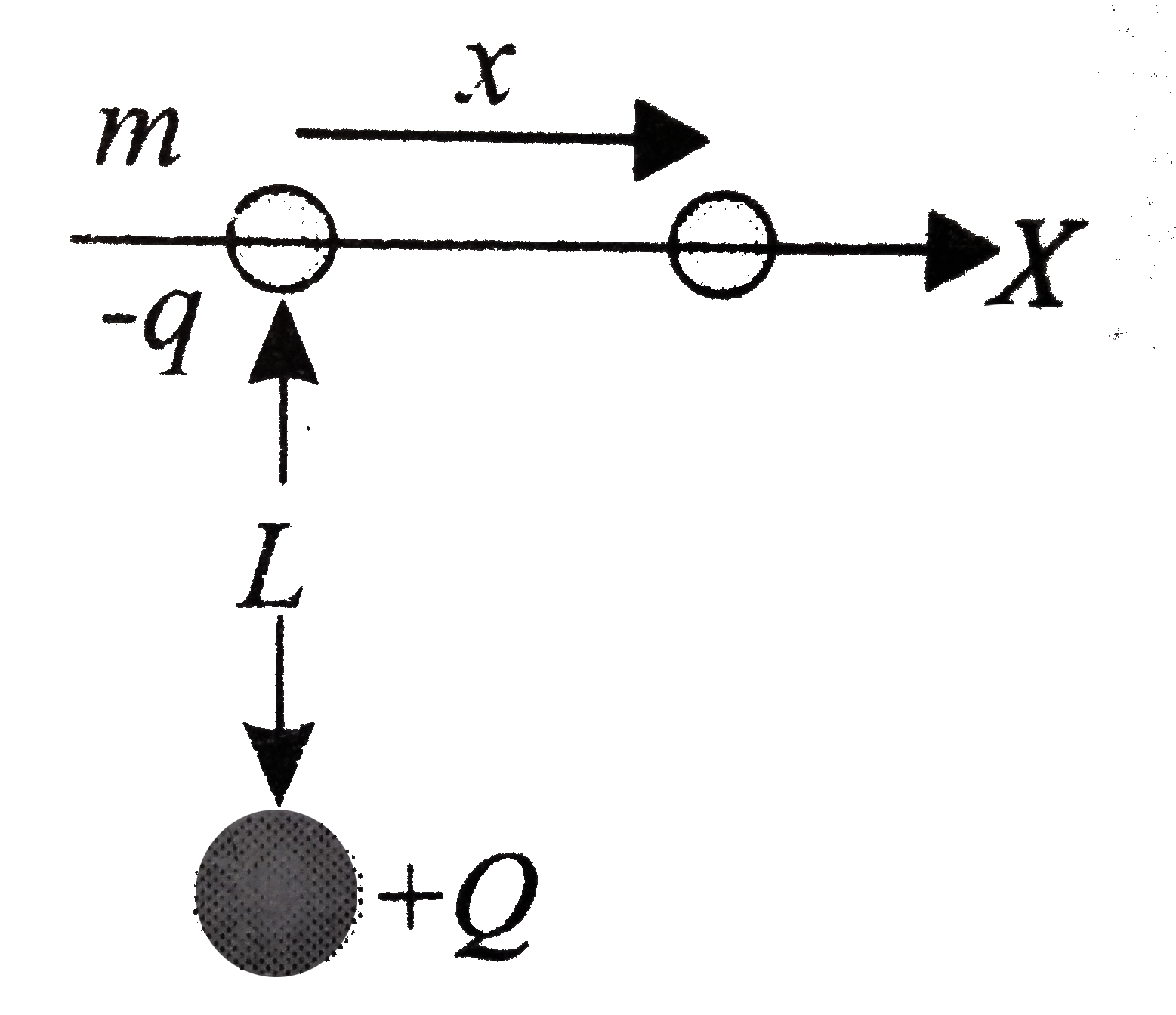
A small beads of mass ma having charge -q is constrained to move along a froctionless wire. A positive charges Q lies at a distance L from the wire. Initiallym the bead is just above charge +Q. Show that if the bead is displaced a distance x, where x<<L, and released, it will exhibit simple harmonic motion. obtain an expression for the tive period of simple harnonic motion.
The correct Answer is:2π√4πε0mL3Qq.
Components F cos θ of attractive coulomb's force restores the charge q to its mean positon O.
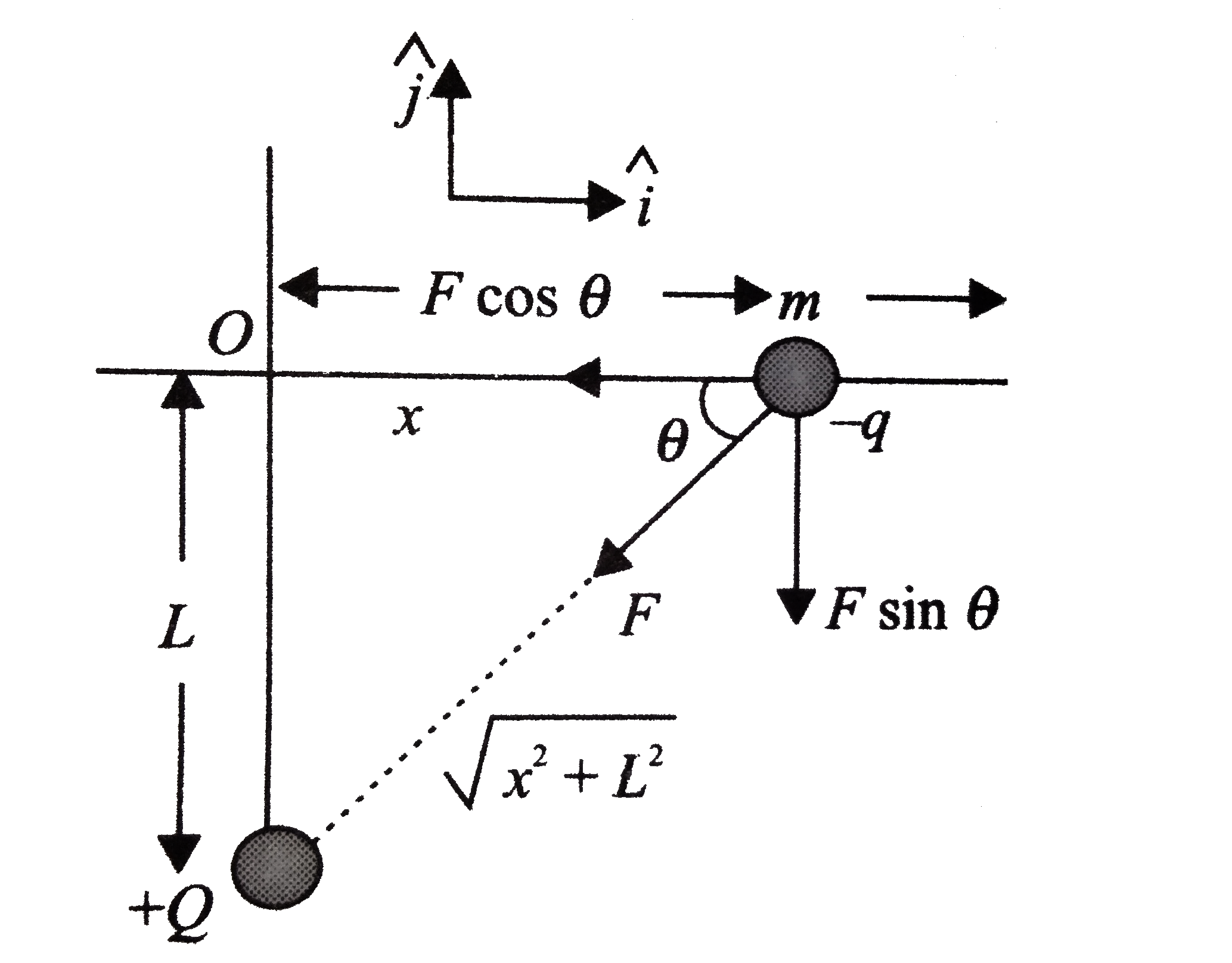
From Newton's second law,
−Fcosθ=ma
or, Qq4πε0(x2+L2)x√x2+L2=ma
or, a=Qq4πε0mx(x2+L2)3/2
For a small linear displacement , x<<L, we can ignore x2 in conparison to L2.
a≅−Qq4πε0mL3x
which is equation of SHM with ω=√Qq4πε0mL3
T=2πω=2π√4πε0mL3Qq.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
A small point mass m has a charge q, which is constrained to move inside a narrow frictionless cylinder, At the bae of the cylinder is point mass of charge Q having the same sign as q. If the mass m is displaced by a small amount from its equilibrium position and released. it will exhibit simple harmonic motion. Find the angular frequency of the mass?

View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View SolutionThree equal negative charges, −q1 each form the vertices of and equilateral triangle . A particle of mass m and a positive charge q2 is constrained to move along a line perpendicular to the plane of triangle and through its center, which at a distance r from each of the negative charges as shown in fig. The whole systen is kept in gravity-free space, Find the time period of vibration of the particle for small displacement from the equilibrium position.

View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionTwo indentical point charges having magnitude q each are placed as shown if fig. If we place a negative cahrge (of magnitude -q and mass m)at the midpoint of charges and displaced along the x-axis, examine whether it will perform simpe harmonic motion. If yes then find the time period of oscillation of the particle.

View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
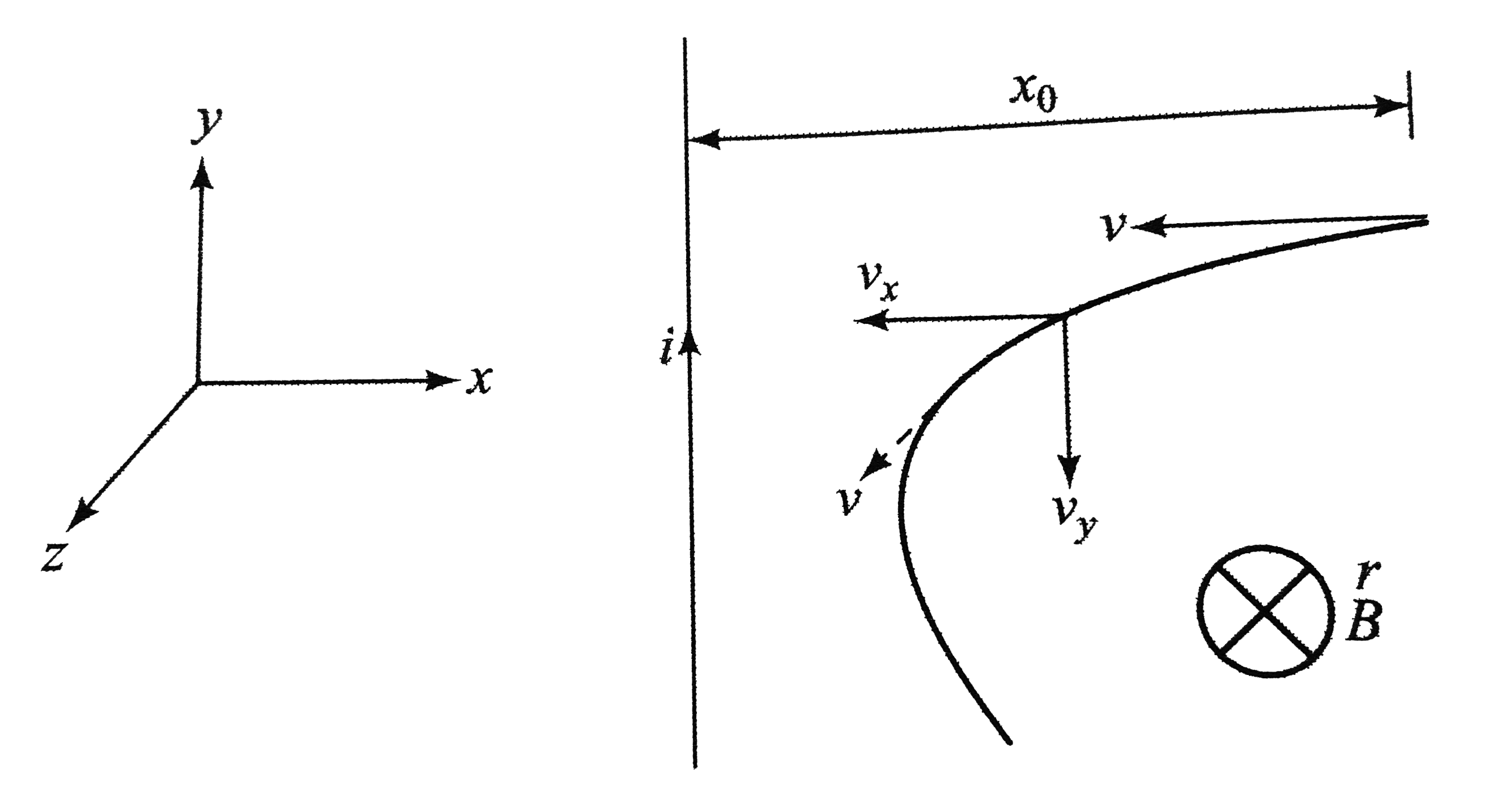

View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
View SolutionA particle of mass m and charge −Q is constrained to move along the axis of a ring of radius a. The ring carries a uniform charge density +λ along its length. Initially, the particle is in the centre of the ring where the force on it is zero. Show that the period of oscillation of the particle when it is displaced slightly from its equilibrium position is given by
T=2πsq√2ε0ma2λQ
View SolutionThree infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d
i find the locus of the points for which the magnetic field B is zero.
ii If the central wire is displaced along the z-direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is λ, find the frequency of oscillation.
View SolutionA thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.

View Solution
