A plate moves normally with the speed v1 towads a horizontal jet of uniform area of cross-section. The jet discharge water at the rate of volume V per second at a speed of v2. The density of water is ρ. Assume that water splashes along the surface of the plate ar right angles to the original motion. The magnitude of the force action on the plate due to the jet of water is
ρVv1
ρVv2(v1+v2)2
pVv1_v2(v1)2
pV(v1+v2)
The correct Answer is:D
To solve the problem, we need to determine the magnitude of the force acting on the plate due to the water jet. We can approach this step by step.
Step 1: Understand the scenario
The plate is moving towards a horizontal jet of water with speed v1. The jet discharges water at a speed v2 and at a rate of volume V per second. The water splashes off the plate at right angles to its original motion.
Step 2: Identify the relevant physics concepts
The force exerted by the water jet on the plate can be calculated using the principle of momentum. The force is equal to the rate of change of momentum of the water hitting the plate.
Step 3: Write the formula for force
The force F can be expressed as:
F=dPdt
where P is the momentum.
Step 4: Define momentum
Momentum P is defined as:
P=m⋅v
where m is the mass and v is the velocity.
Step 5: Determine the change in momentum
The change in momentum ΔP for the water hitting the plate can be calculated. Since the water is moving towards the plate with speed v2 and the plate is moving towards the water with speed v1, the effective change in velocity when the water splashes off the plate is:
Δv=v1+v2
Step 6: Calculate the mass flow rate
The mass flow rate of water can be expressed in terms of density ρ and the volume flow rate V:
Mass flow rate=ρ⋅V
Step 7: Substitute into the force equation
Substituting the mass flow rate and the change in velocity into the force equation gives:
F=mass flow rate⋅Δv=ρV(v1+v2)
Step 8: Final expression for force
Thus, the magnitude of the force acting on the plate due to the jet of water is:
F=ρV(v1+v2)
Conclusion
The force acting on the plate due to the jet of water is given by the formula:
F=ρV(v1+v2)
The plate is moving towards a horizontal jet of water with speed v1. The jet discharges water at a speed v2 and at a rate of volume V per second. The water splashes off the plate at right angles to its original motion.
The force exerted by the water jet on the plate can be calculated using the principle of momentum. The force is equal to the rate of change of momentum of the water hitting the plate.
The force F can be expressed as:
F=dPdt
where P is the momentum.
Momentum P is defined as:
P=m⋅v
where m is the mass and v is the velocity.
The change in momentum ΔP for the water hitting the plate can be calculated. Since the water is moving towards the plate with speed v2 and the plate is moving towards the water with speed v1, the effective change in velocity when the water splashes off the plate is:
Δv=v1+v2
The mass flow rate of water can be expressed in terms of density ρ and the volume flow rate V:
Mass flow rate=ρ⋅V
Substituting the mass flow rate and the change in velocity into the force equation gives:
F=mass flow rate⋅Δv=ρV(v1+v2)
Thus, the magnitude of the force acting on the plate due to the jet of water is:
F=ρV(v1+v2)
The force acting on the plate due to the jet of water is given by the formula:
F=ρV(v1+v2)
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A flat plate moves normally towards a discharging jet of water at the rate of 3m/s. The jet discharges the water at the rate of 0.1m3/s and at the speed of 18m/s. The force exerted on the plate due to the jet is
View SolutionThe horizontal speed of a jet of water is 100 cm/sec and 50cm3 of water hits the plate each second. Assume that the water moves parallel to the plate after striking it. The force exerted on the stationary plate if it is held perpendicular to the jet of water is :
View SolutionThe fire fighters attach brass jets at the end of water pipes. Why?
View SolutionA horizontal jet of water coming out of a pipe of area of cross - section 20 cm2 hits a vertical wall with a velocity of 10 ms−1 and rebounds with the same speed. The force exerted by water on the wall is,
View SolutionWater flows steadily through a horizontal pipe of a variable cross-section. If the pressure of the water is p at a point , where the speed of the flow is v. What is the pressure at another point , where the speed of the flow is 2 v ? Let the density of water be 1gcm−3.
View SolutionWhich one emits jet of water when disturbed
View SolutionPerforated surface plate of water vascular system is
View Solution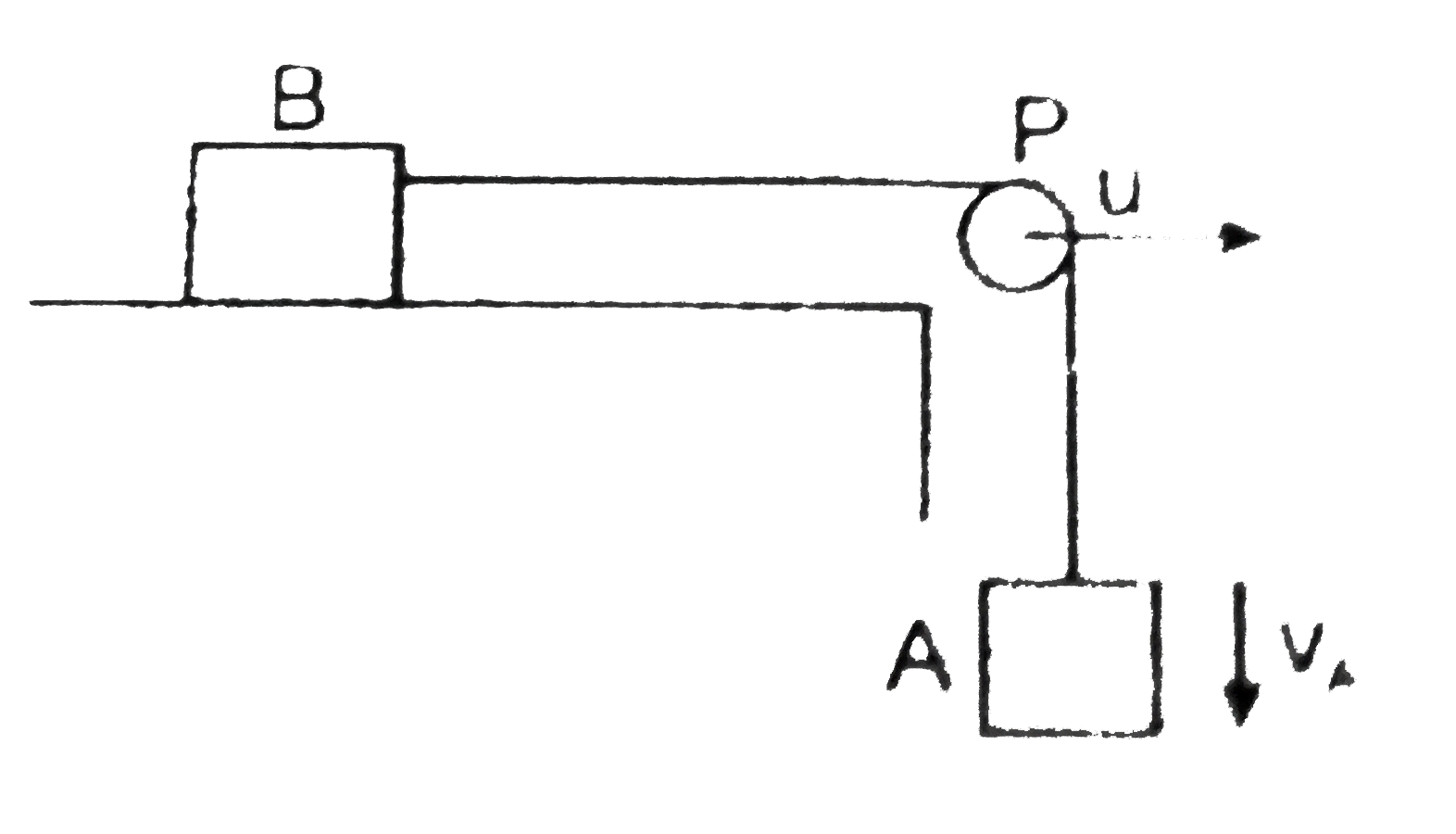
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.
View SolutionA parallel plate capacitors of plate area A has a total surface charge density +σ on one plate and a total surface charge density −σ on the other plate. The force one plate due to the other plate is given by :
View SolutionIn a certain gravity free space, the piston of an injection is being pushed so that the water jet comes out with a speed v. The area of the piston is much greater than the orifice of the injection.
View Solution
