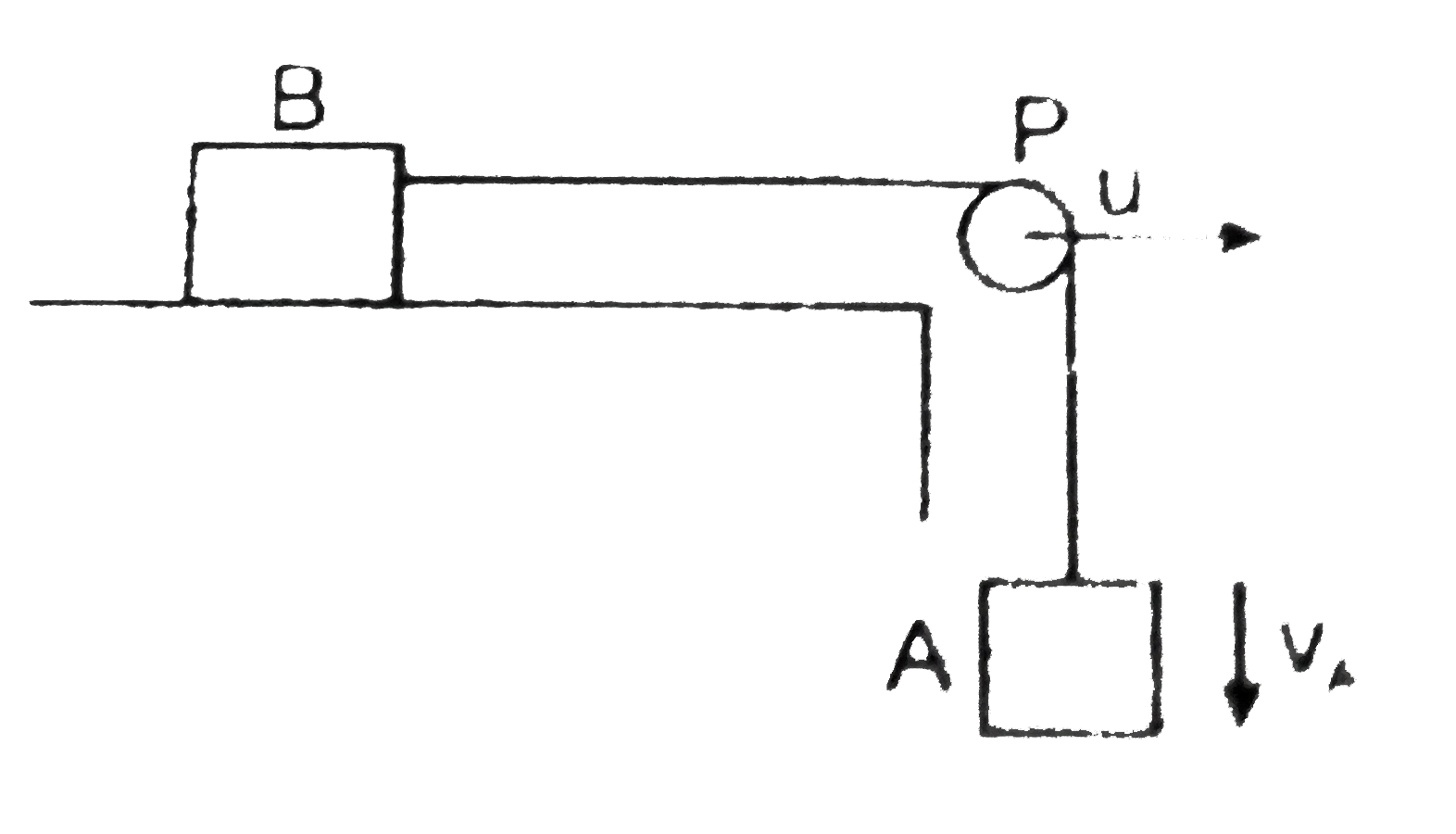
In the figure the pulley P moves to the right with a constant speed u. The downward speed of A is vA and the speed of B to the right VB.
VB=VA
VB=u+VA
VB+u=VA
the two blocks have acceleration of the same magnitude.
The correct Answer is:B, D
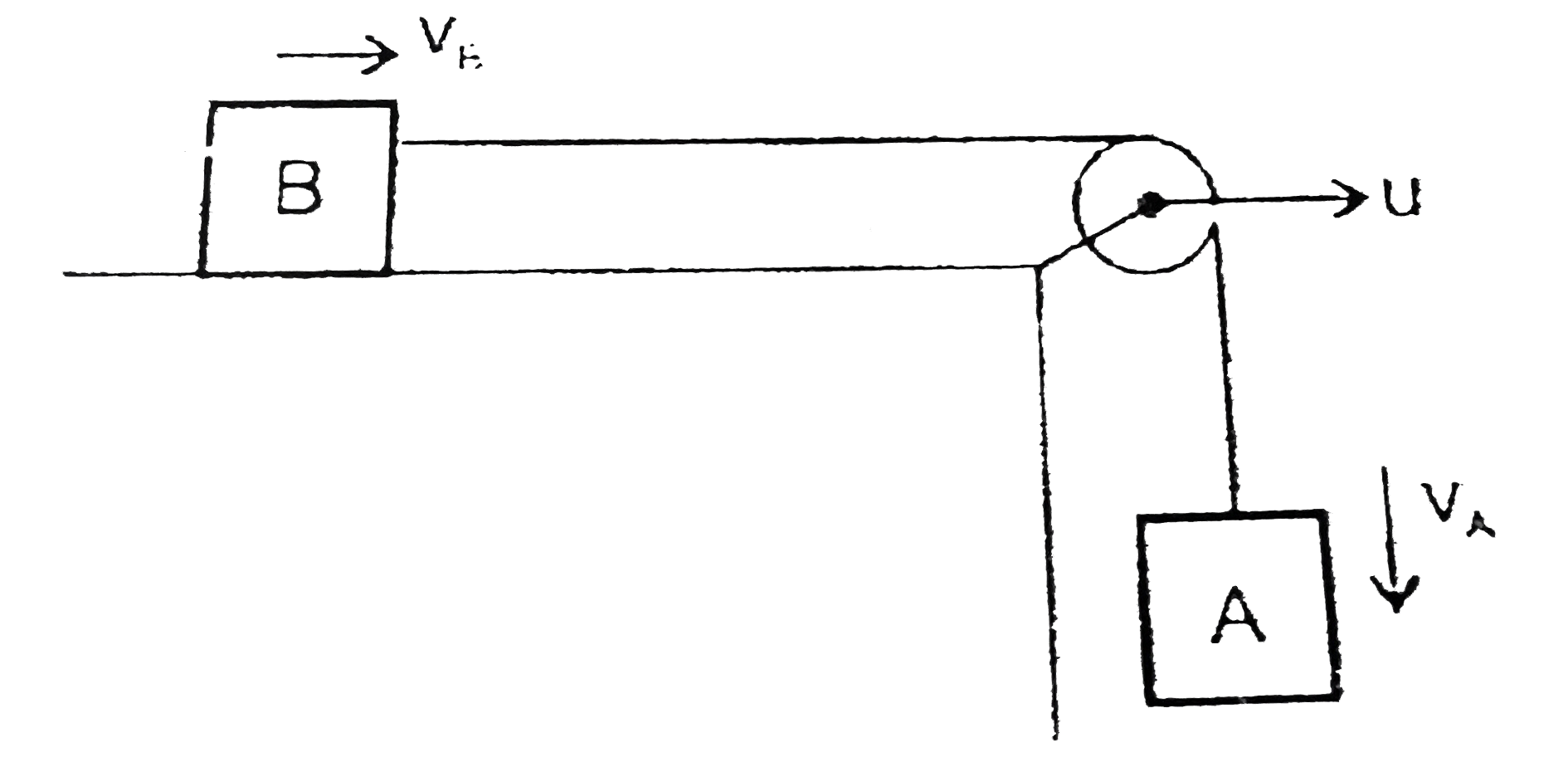
By string constrain
vA+u−VB=0
or vB=u+aB
differentiating both side
aB=0+aA
Similar Questions
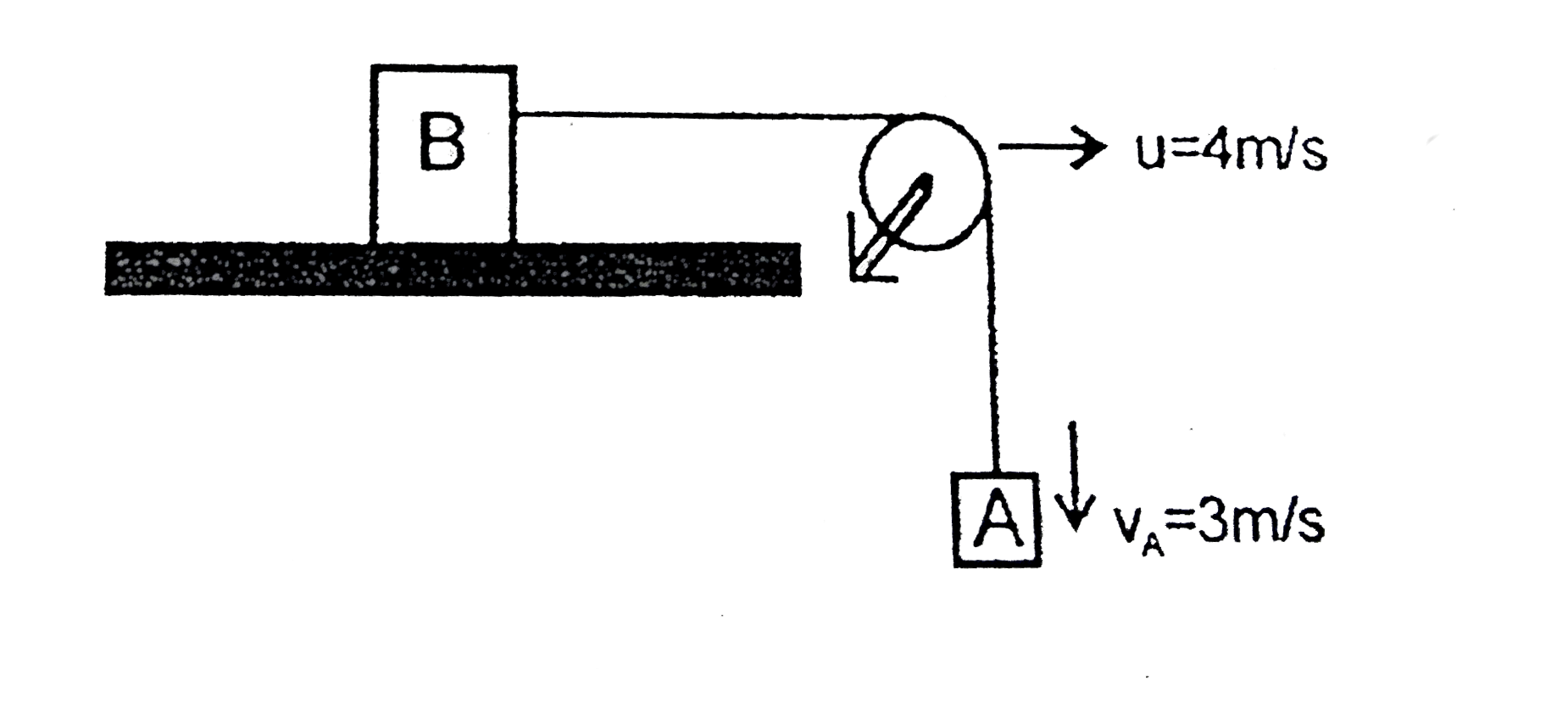
In the figure, the pulley P moves to the right with a constant speed of 4m/s. The downward speed of A is vA=3m/s. Then find the speed of B of the right (in m/s).
 View Solution
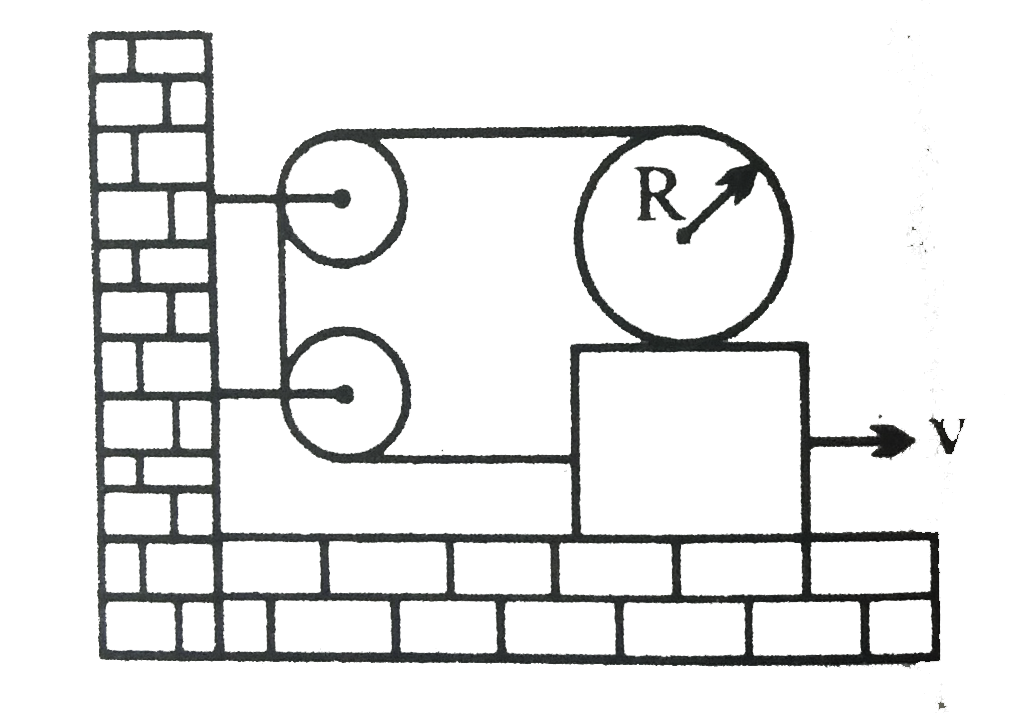
View SolutionIn the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then:
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Two particles A and B, initially at rest, moves towards each other under a mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2 v, the speed of centre of mass is
AzeroBvC1.5 vD3 v - Question 2 - Select One
Two particles A and B intiallly at rest, move towards each other under a mutual force of attraction. AT the instant when the speed of A is v and the speed of B is 2 v, the speed of the centre of mass of the system is
AzeroBvC1.5 vD3 v - Question 3 - Select One
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
Block B moves to the right with a constant velocity v0. The velocity of body a relative to b is
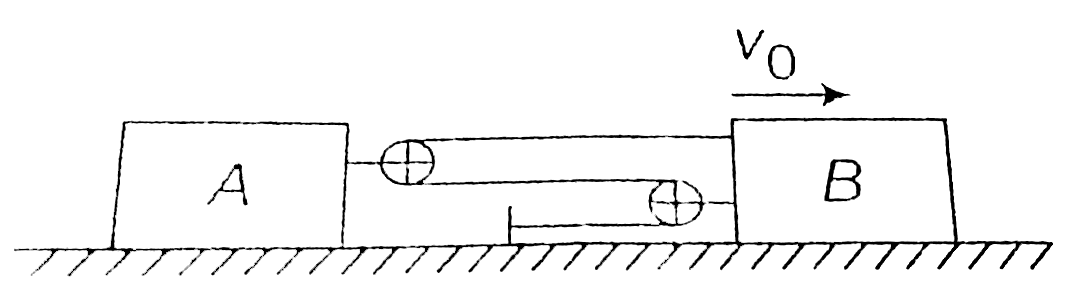 View Solution
View Solution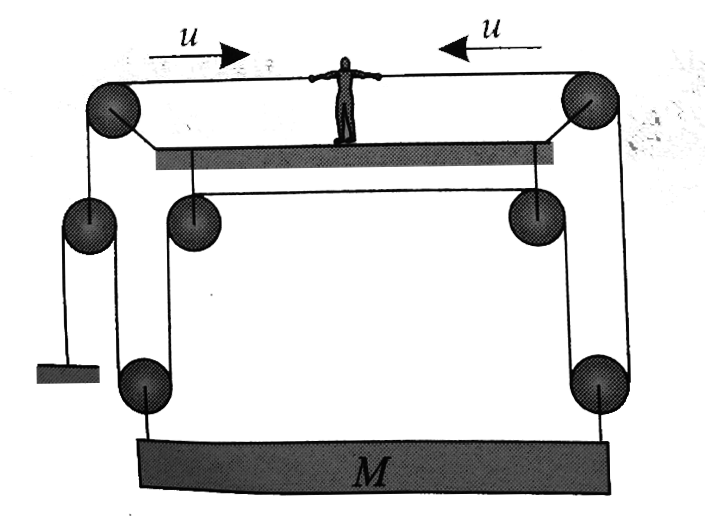
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.View Solution
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.View SolutionA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
View Solution
A lift is moving upwards with a constant speed of 5ms. The speed of one of the pulleys is 5ms as shown. Then the speed of second pulley is:View Solution
