A thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to

√3−12−√3
√3+12+√3
√3−1√3+1
√3+1√3−1
The correct Answer is:D
tanθ=ρ1−ρ2ρ1+ρ2=tan30∘=1√3
Solving this equation we get,
ρ1ρ2=√3+1√3−1
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
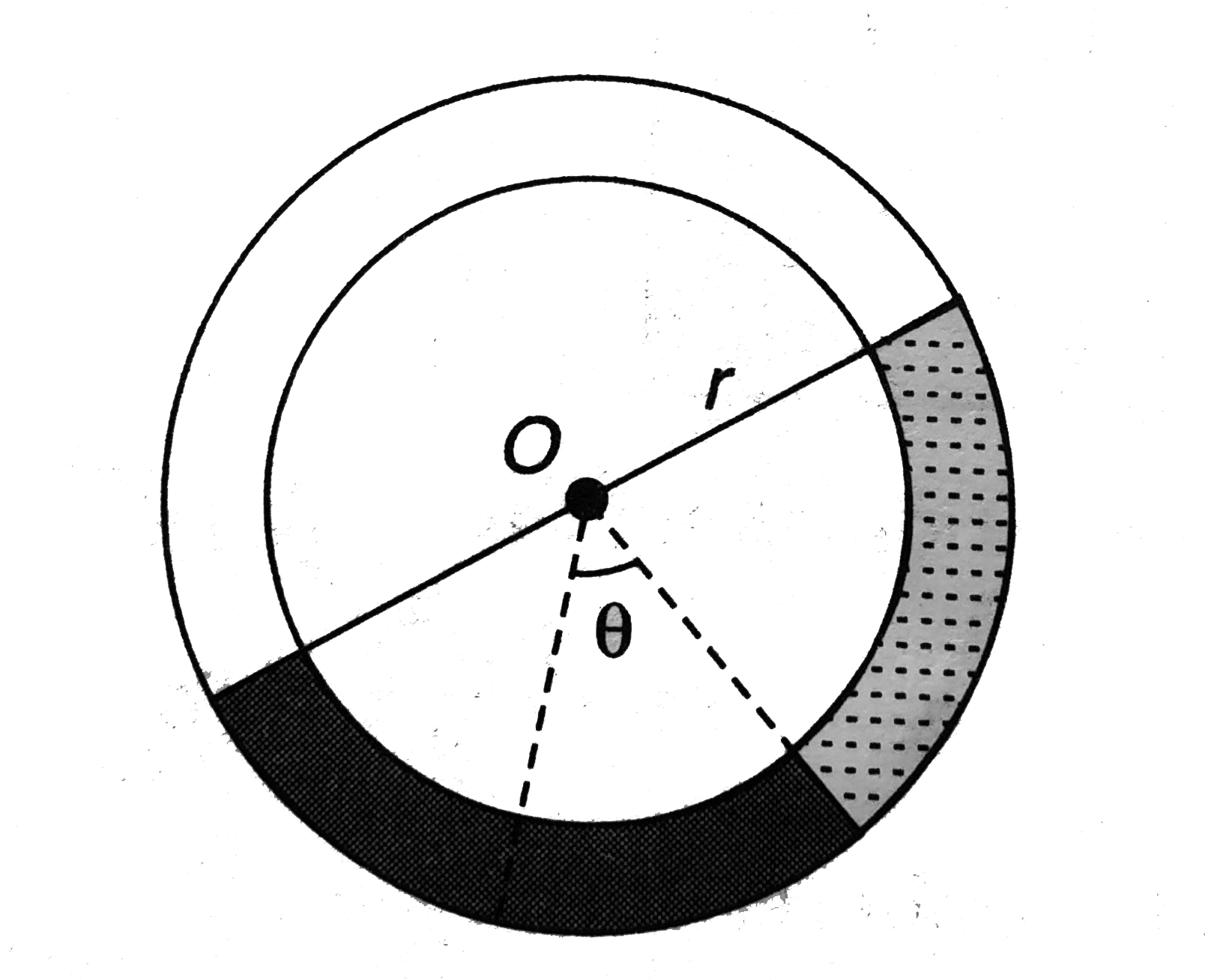
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
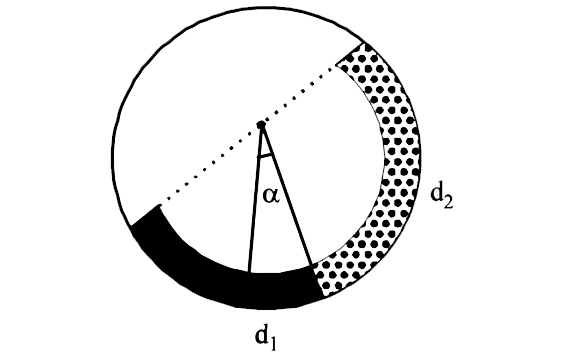
View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1andd2 are filled in the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface make an angle α with vertical. Ratio d1d2 is :
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
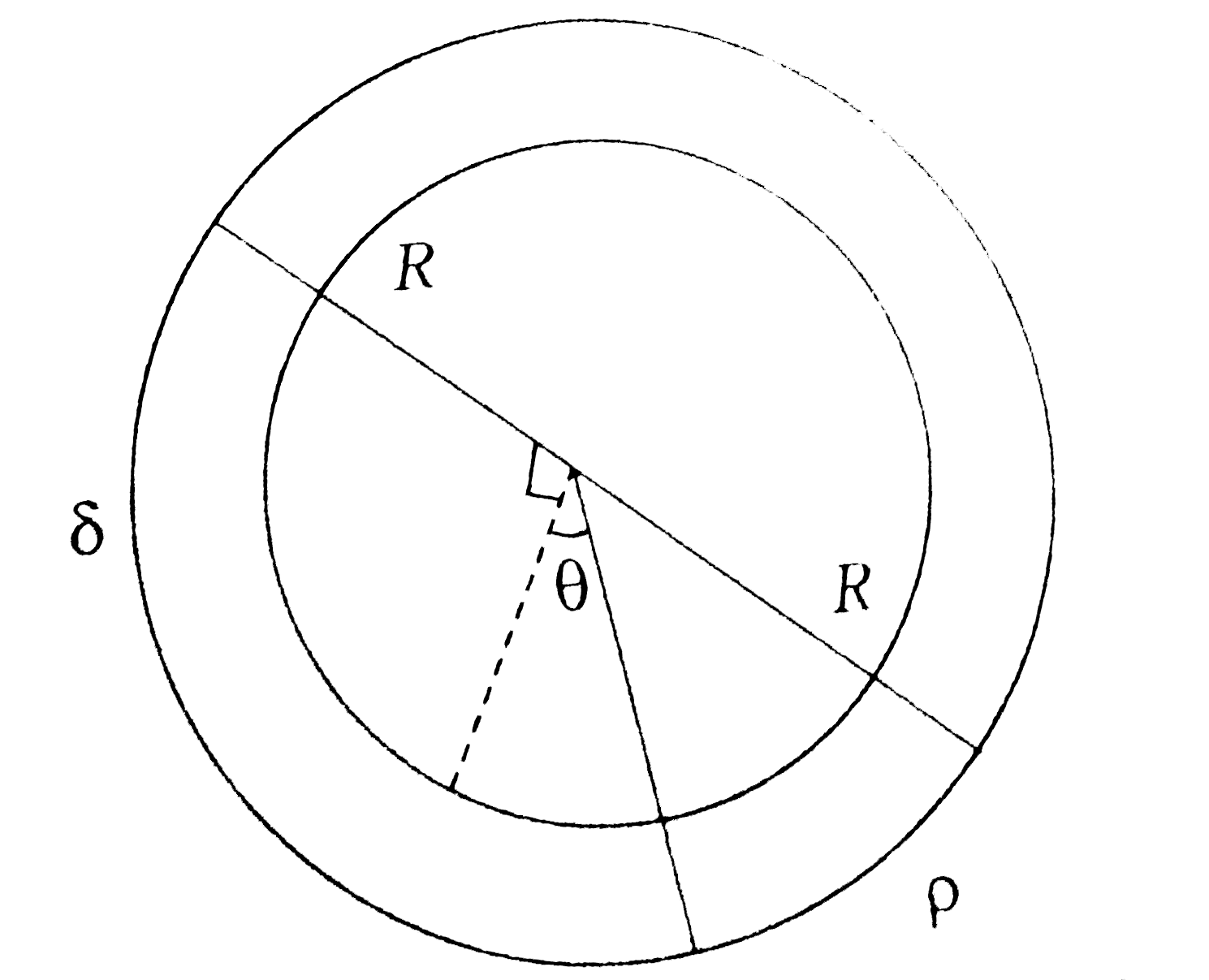
View SolutionA uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
View SolutionEqual volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
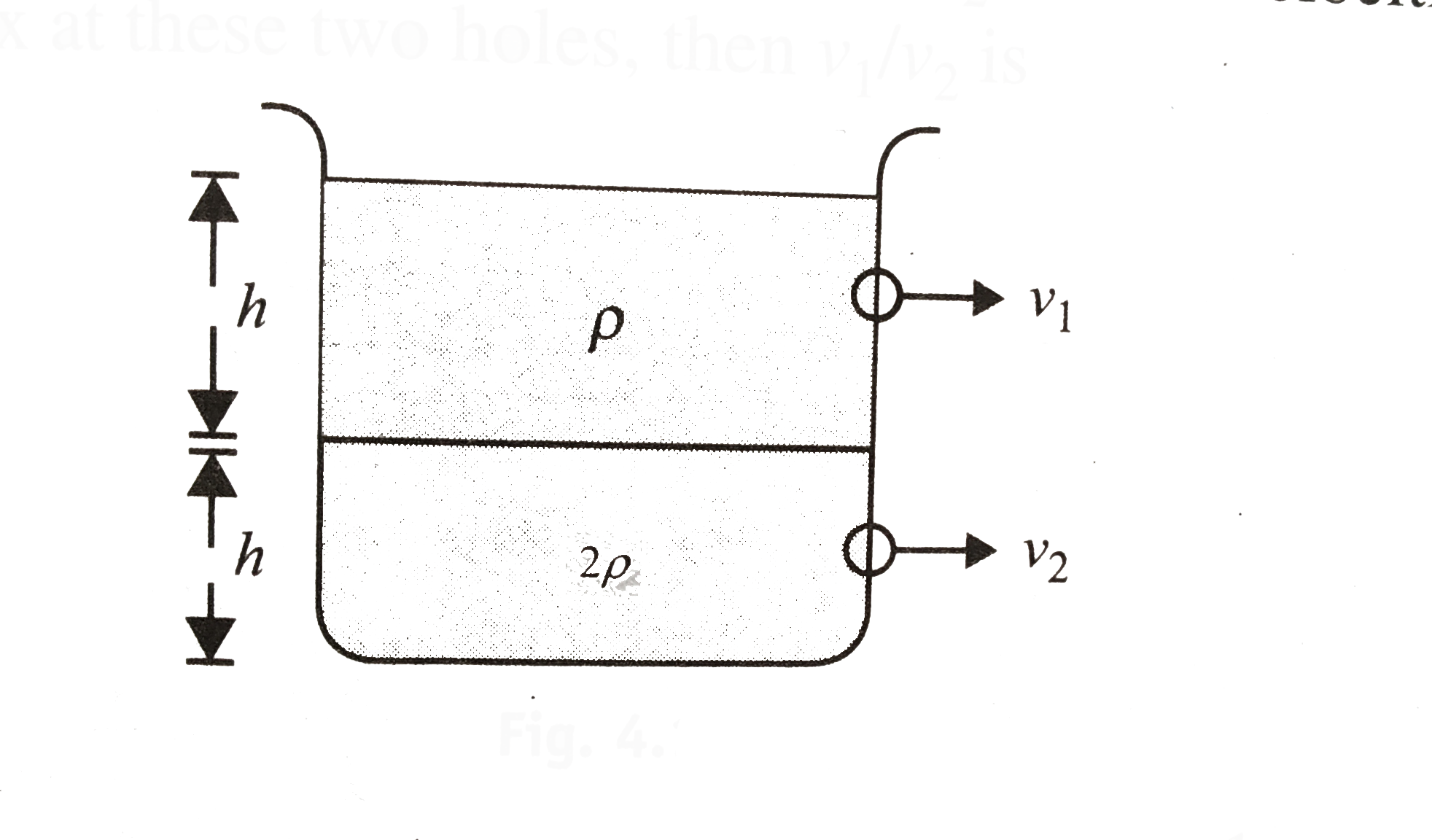
View SolutionEqual volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
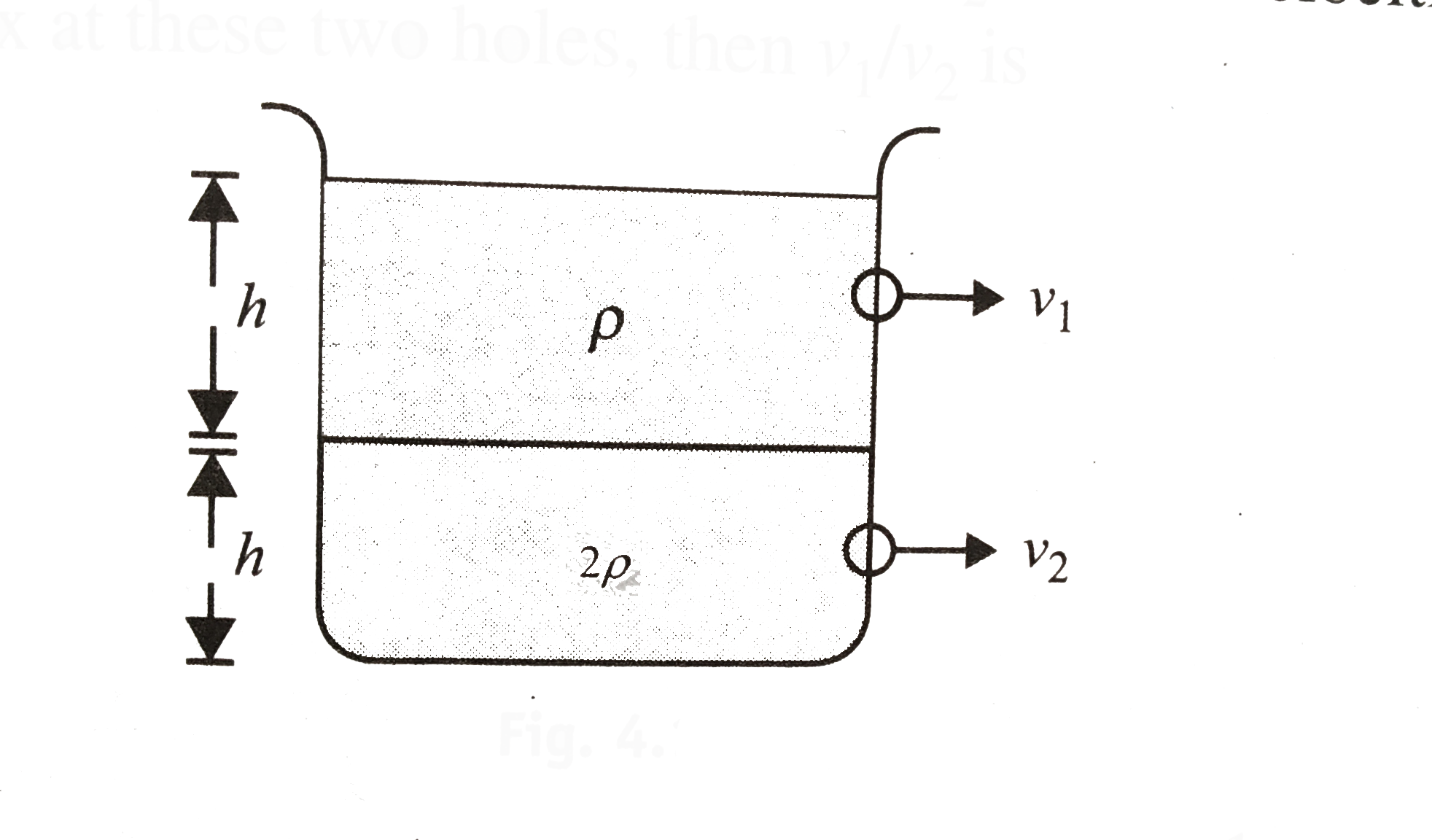
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

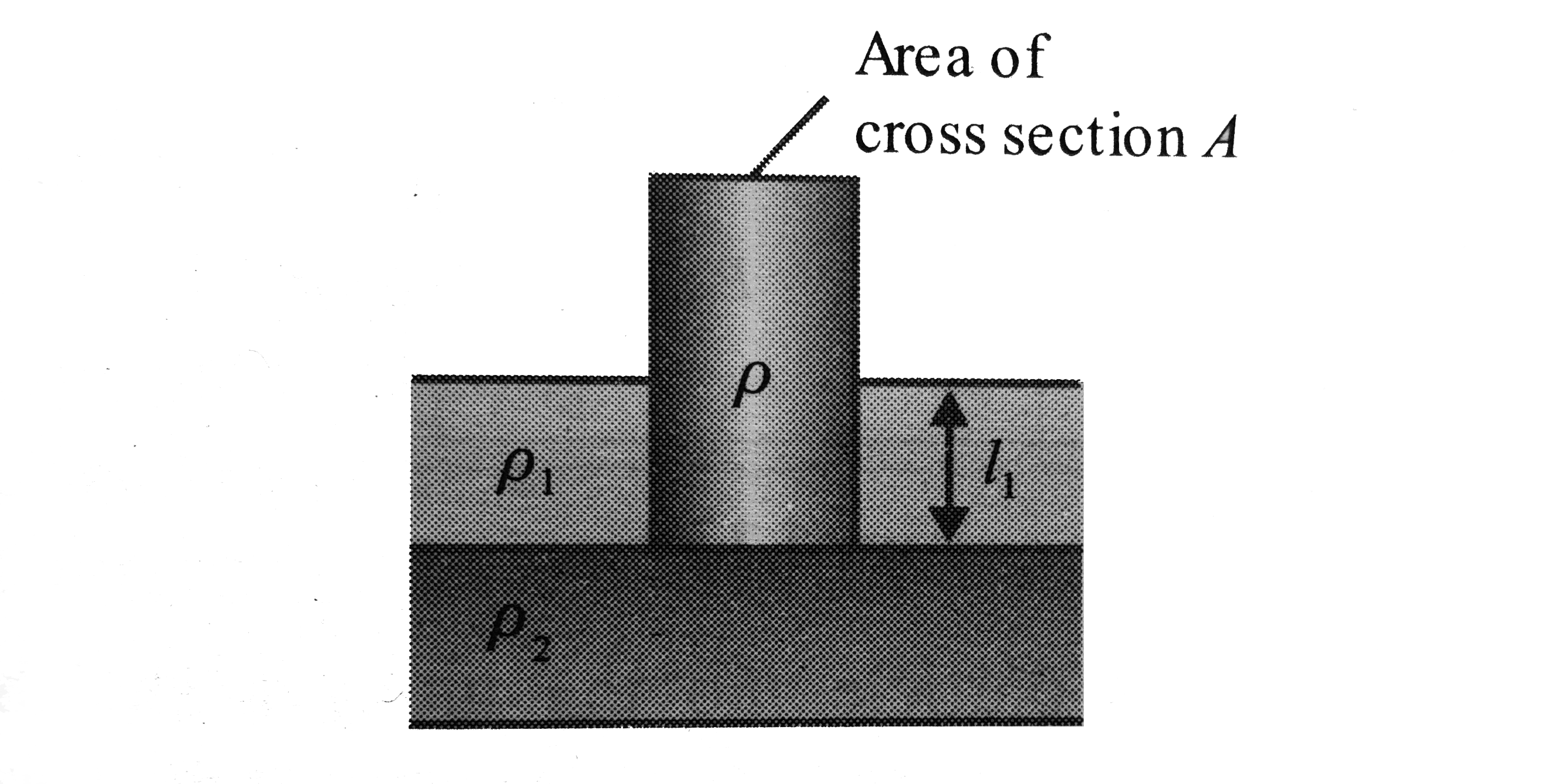
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
View SolutionEqual volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is
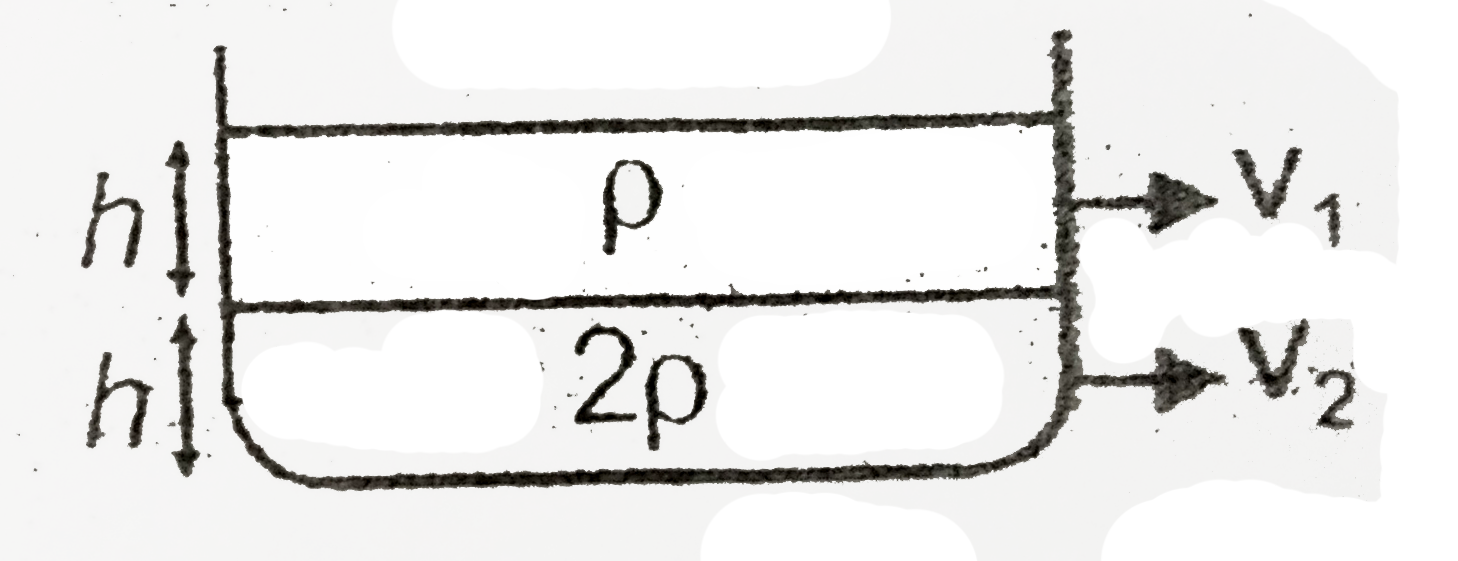
View Solution
