A spring balance reads 10kg when a bucket of water is suspened from it . What will be the reading of the balance when an iron piece of mass 7.2kg suspended by a string is immersed with half its volume inside the water in the bucket? Relative density of iron is 7.2 a) 10 kg b) 10.5 kg c) 13.6 kg d) 17.2 kg
10kg
10.5kg
13.6kg
17.2kg
The correct Answer is:B
To solve the problem, we need to determine the reading of the spring balance when a bucket of water is suspended from it, and an iron piece is immersed in the water. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
The spring balance reads 10kg when the bucket of water is suspended. This means the weight of the bucket of water is equivalent to 10kg under the influence of gravity.
Step 2: Calculate the Weight of the Iron Piece
The mass of the iron piece is 7.2kg. The weight (W) of the iron piece can be calculated using the formula:
\( W = m \cdot g \)
Where:
- \( m = 7.2 \, \text{kg} \)
- \( g \approx 9.8 \, \text{m/s}^2 \) (acceleration due to gravity)
Thus, the weight of the iron piece is:
\( W = 7.2 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 = 70.56 \, \text{N} \)
Step 3: Calculate the Buoyant Force on the Iron Piece
The relative density of iron is given as 7.2, which means the density of iron is 7.2 times the density of water. The density of water (\( \rho_w \)) is approximately \( 1000 \, \text{kg/m}^3 \), so:
\( \text{Density of iron} = 7.2 \cdot 1000 \, \text{kg/m}^3 = 7200 \, \text{kg/m}^3 \)
The volume (V) of the iron piece can be calculated using its mass and density:
\( V = \frac{m}{\text{Density}} = \frac{7.2 \, \text{kg}}{7200 \, \text{kg/m}^3} = 0.001 \, \text{m}^3 \)
Since half of the iron piece is immersed in water, the volume of the submerged part is:
\( V_{\text{submerged}} = \frac{1}{2} \cdot 0.001 \, \text{m}^3 = 0.0005 \, \text{m}^3 \)
The buoyant force (F_b) can be calculated using Archimedes' principle:
\( F_b = V_{\text{submerged}} \cdot \rho_w \cdot g \)
Substituting the values:
\( F_b = 0.0005 \, \text{m}^3 \cdot 1000 \, \text{kg/m}^3 \cdot 9.8 \, \text{m/s}^2 = 4.9 \, \text{N} \)
Step 4: Calculate the Effective Weight of the Iron Piece
The effective weight of the iron piece when it is submerged is given by:
\( \text{Effective Weight} = \text{Weight of Iron} - \text{Buoyant Force} \)
\( \text{Effective Weight} = 70.56 \, \text{N} - 4.9 \, \text{N} = 65.66 \, \text{N} \)
Step 5: Calculate the Total Weight on the Spring Balance
The total weight on the spring balance is the weight of the bucket of water plus the effective weight of the iron piece:
\( \text{Total Weight} = \text{Weight of Bucket} + \text{Effective Weight} \)
Converting the weight of the bucket from kg to N (using \( g \)):
\( \text{Weight of Bucket} = 10 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 = 98 \, \text{N} \)
Thus:
\( \text{Total Weight} = 98 \, \text{N} + 65.66 \, \text{N} = 163.66 \, \text{N} \)
Step 6: Convert Total Weight Back to kg
To convert the total weight back to kg, we divide by \( g \):
\( \text{Total Weight in kg} = \frac{163.66 \, \text{N}}{9.8 \, \text{m/s}^2} \approx 16.67 \, \text{kg} \)
Conclusion
The reading of the balance will be approximately 16.67kg, which is closest to option (d) 17.2kg.
The spring balance reads 10kg when the bucket of water is suspended. This means the weight of the bucket of water is equivalent to 10kg under the influence of gravity.
The mass of the iron piece is 7.2kg. The weight (W) of the iron piece can be calculated using the formula:
\( W = m \cdot g \)
Where:
- \( m = 7.2 \, \text{kg} \)
- \( g \approx 9.8 \, \text{m/s}^2 \) (acceleration due to gravity)
\( W = 7.2 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 = 70.56 \, \text{N} \)
The relative density of iron is given as 7.2, which means the density of iron is 7.2 times the density of water. The density of water (\( \rho_w \)) is approximately \( 1000 \, \text{kg/m}^3 \), so:
\( \text{Density of iron} = 7.2 \cdot 1000 \, \text{kg/m}^3 = 7200 \, \text{kg/m}^3 \)
\( V = \frac{m}{\text{Density}} = \frac{7.2 \, \text{kg}}{7200 \, \text{kg/m}^3} = 0.001 \, \text{m}^3 \)
\( V_{\text{submerged}} = \frac{1}{2} \cdot 0.001 \, \text{m}^3 = 0.0005 \, \text{m}^3 \)
\( F_b = V_{\text{submerged}} \cdot \rho_w \cdot g \)
Substituting the values:
\( F_b = 0.0005 \, \text{m}^3 \cdot 1000 \, \text{kg/m}^3 \cdot 9.8 \, \text{m/s}^2 = 4.9 \, \text{N} \)
The effective weight of the iron piece when it is submerged is given by:
\( \text{Effective Weight} = \text{Weight of Iron} - \text{Buoyant Force} \)
\( \text{Effective Weight} = 70.56 \, \text{N} - 4.9 \, \text{N} = 65.66 \, \text{N} \)
The total weight on the spring balance is the weight of the bucket of water plus the effective weight of the iron piece:
\( \text{Total Weight} = \text{Weight of Bucket} + \text{Effective Weight} \)
Converting the weight of the bucket from kg to N (using \( g \)):
\( \text{Weight of Bucket} = 10 \, \text{kg} \cdot 9.8 \, \text{m/s}^2 = 98 \, \text{N} \)
\( \text{Total Weight} = 98 \, \text{N} + 65.66 \, \text{N} = 163.66 \, \text{N} \)
To convert the total weight back to kg, we divide by \( g \):
\( \text{Total Weight in kg} = \frac{163.66 \, \text{N}}{9.8 \, \text{m/s}^2} \approx 16.67 \, \text{kg} \)
The reading of the balance will be approximately 16.67kg, which is closest to option (d) 17.2kg.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 More Than One Correct
Explore 10 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Level 2 Comprehension Based
Explore 7 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Subjective Question
Explore 2 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
Knowledge Check
The spring balance A read 2 kg with a block m suspended from it. A balance B reads 5 kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging is inside the liquid in the beaker as shown in Fig. 15.5.3. In this situation
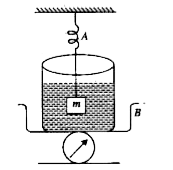 Athe balance A will read more than 2 kgBthe balance B will read more than 5 kgCthe balance A will read less than 2 kg and B will more than 5 kgDthe balance A and B will read 2 kg and 5 kg respectively.
Athe balance A will read more than 2 kgBthe balance B will read more than 5 kgCthe balance A will read less than 2 kg and B will more than 5 kgDthe balance A and B will read 2 kg and 5 kg respectively.
Two 10 kg bodies are attached to a spring balance as shown in figure. The reading of the balance will be:
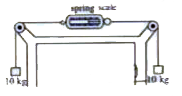
View SolutionA block of mass 10 kg is suspended throug two light spring balances as shown in figure

View SolutionA wire gets elongated by 4 mm when a block of mass 2 kg is suspended from it. Now, the block is immersed in water, the wire contracts by 1 mm. Find the density of block when the density of water is 1000kg/m3.
View SolutionFind the mass of 555cm3 of iron in kg when density of iron is 7.6g/cm3.
View SolutionA spring balance is found to have a period of oscillation of 3.14 s, when a 12 kg weight is suspended from it. How much does the spring elongate when a 2 kg weight is suspended from it ?
View SolutionThe spring balance A reads 2 kg with a block m suspended from it. A balance B reads 5kg when a beaker with liquid is put on the pan of the balance. The two balances are now so arranged that the hanging mass in inside the liquid in the beaker as shown in the figure. In this situation:
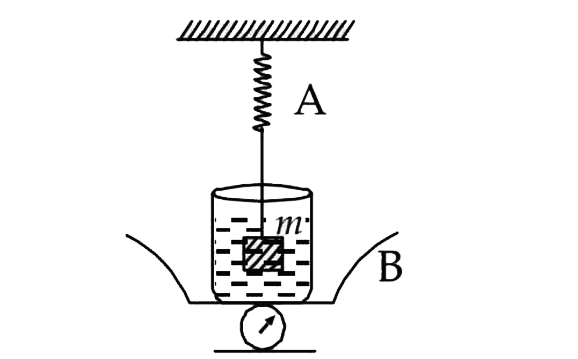
View SolutionA block of silver of mass 4kg hanging from a string is immersed in a liquid of relative density 0.72. If relative density of silver is 10, then tension in the string will be
View Solution
