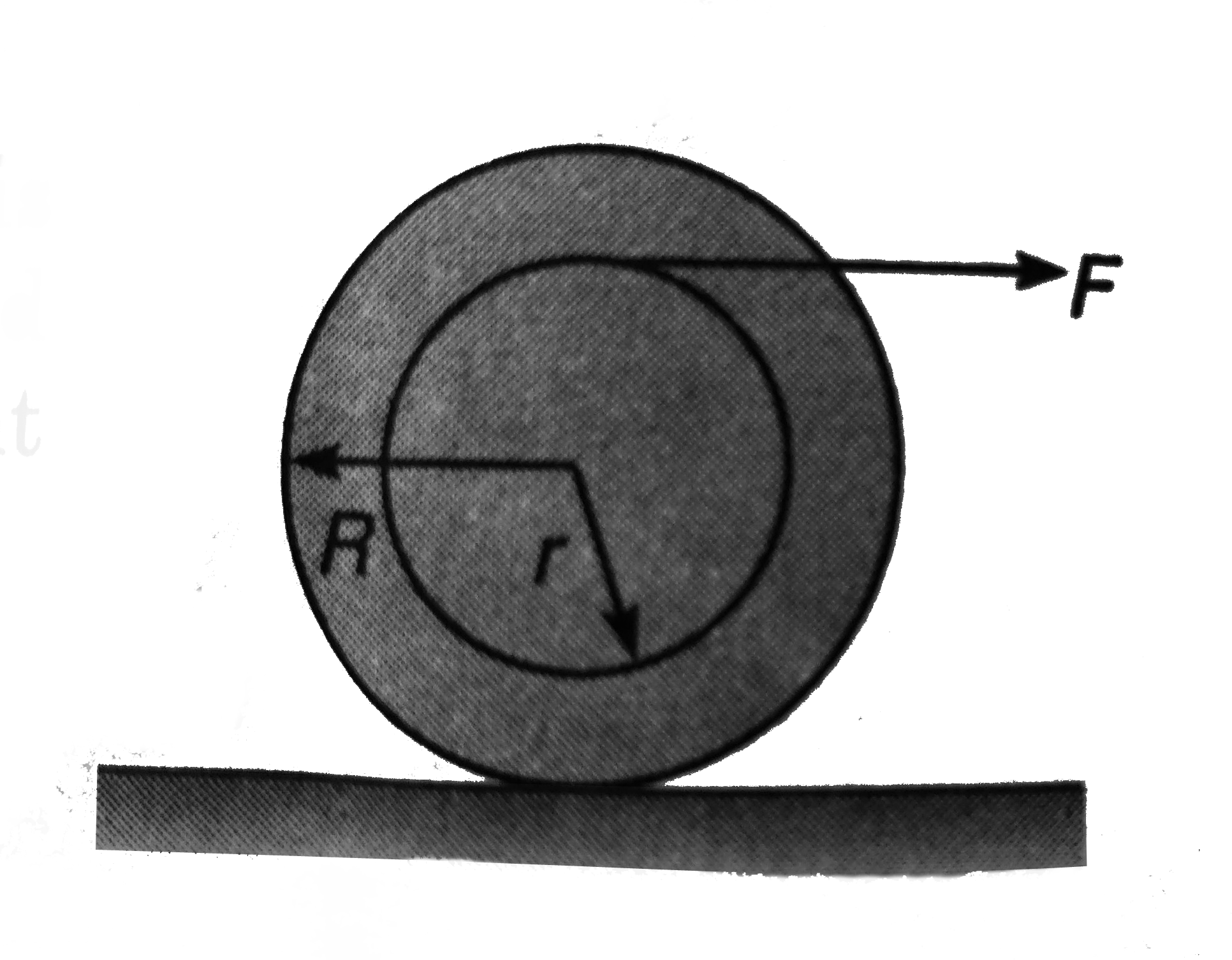
A heavy homogeneous cyliner has mass m and radius R. It is accelerated by a force F which is applied through a rope wound around a light drum of radius r attached to the cylinder (figure) the coefficient of static friction is sufficient for the cylinder to roll without slipping.
Find the friction force.
Find the acceleration a of the centre of the cylinder
it is possible to choose r, so that a is greater than Fm ? How ?
What is the direction of the friction in the circumstances of part(C)?

(a). For pure rolling to take place,
a=Rα or F−fm+R⎡⎣Fr+fR12mR2⎤⎦
Solving this equation we get
f=23(12−rR)
(b). Acceleration a=F−fm
substituting value of f from part (a), we get
a=2F3mR(R+r)
(c). a>Fm if 23R(R+r)>1 or r>R2
(d). In this case force of friction is in forward direction.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions

A uniform solid cylinder having mass M and radius R is pulled by a horiozntal force F acting through the center as shown. The cylinder rolls to the right without slipping. What is the magnitude of the force of friction between the cylinder and the ground?
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
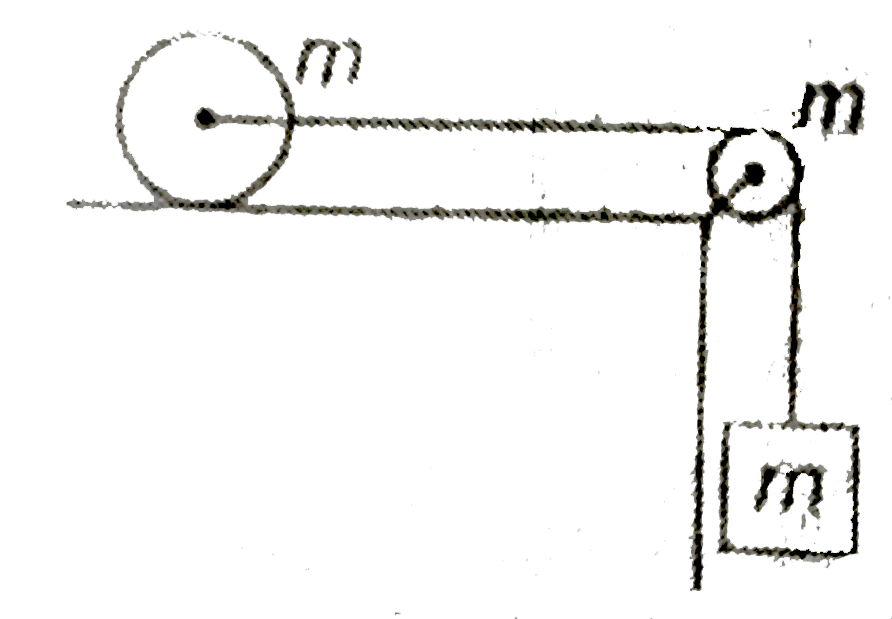
Force of friction acting on the cylinder is
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
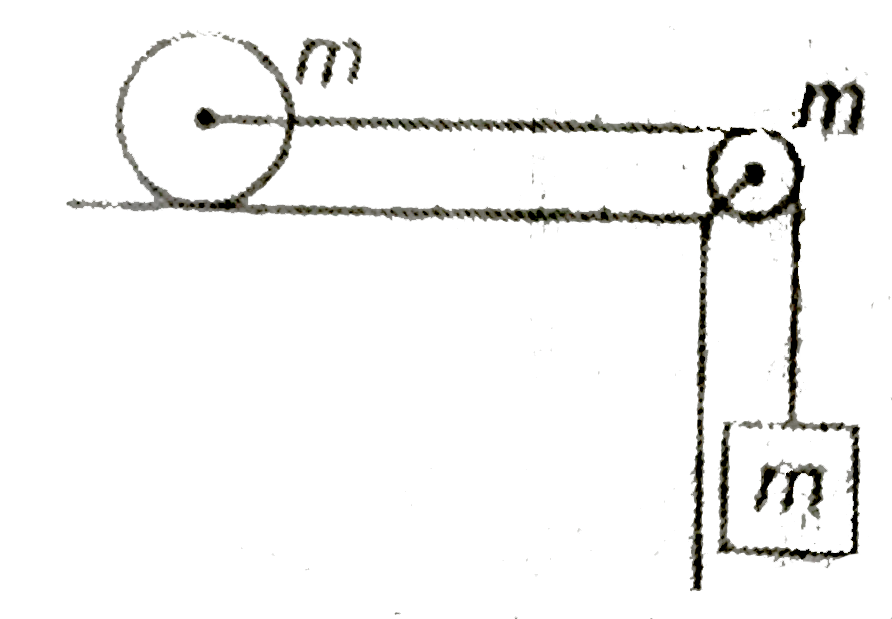
Angular acceleration of the cylinder is
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
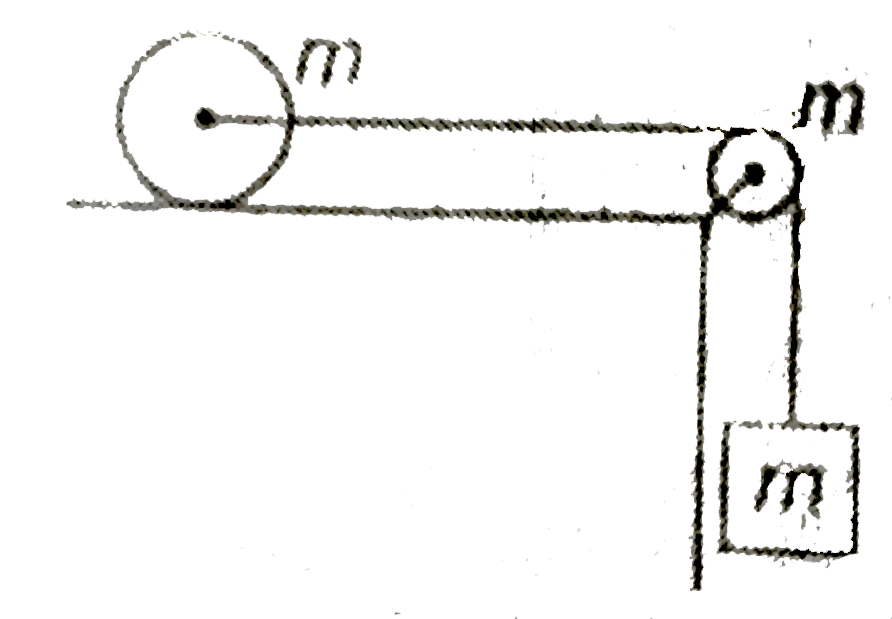
Acceleration of the block is
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA load of mass m is attached to the end of a string wound on a cylinder of mass M and radius R. The string passes round a pulley.
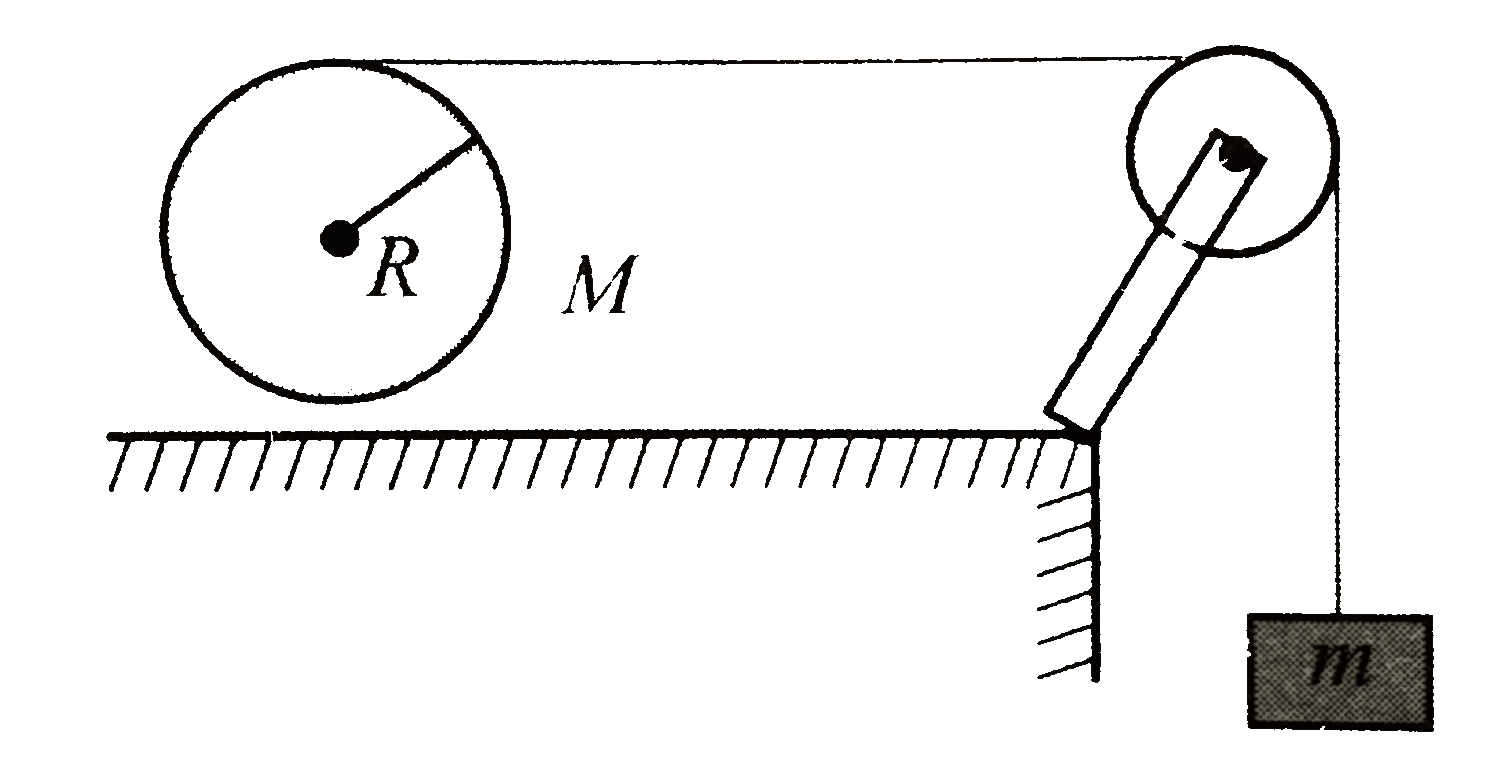
a. Find the acceleration of the cylinder M when it rolls.
b. If the coefficient of friction is μ. Find the accelerative of the cylinder when it slips and rolls.
c. Find the minimum value of coefficient of friction for which the cylinder rolls always
View Solution
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
View Solution
