A cylinder of mass is kept on the edge of a plank of mass and length , which in turn is kept on smooth ground. Coefficient of friction between the plank and the cylinder is . The cylinder is given an impulse, which imparts it a velocity but no angular velocity. Find the time after which the cylinder falls off the plank.

Initially the cylinder will slip on the plank, therefore kinetic energy friction will act between the cylinder and the plank.
For pure rolling
Also,
Hence the remaining distance is travelled in a time
total time
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
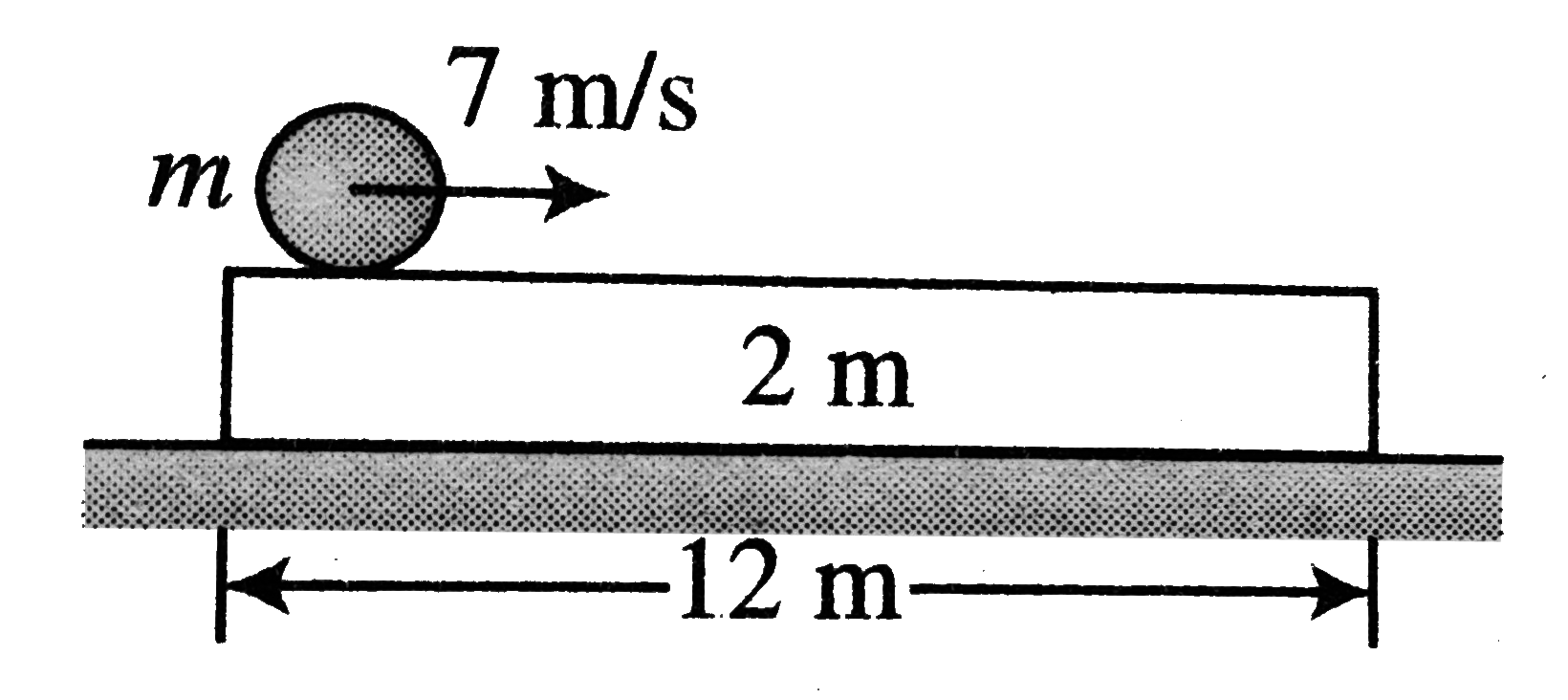
A solid cylinder is kept on one edge of a plank of same mass and length 25 m placed on a smooth surface as shown in the figure. The coefficient of friction between the cylinder and the plank is 0.5. The plank is given a velocity of 20ms−1 towards right. Find the time (in S) after which plank any cylinder will separate. [g=10ms−2]

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
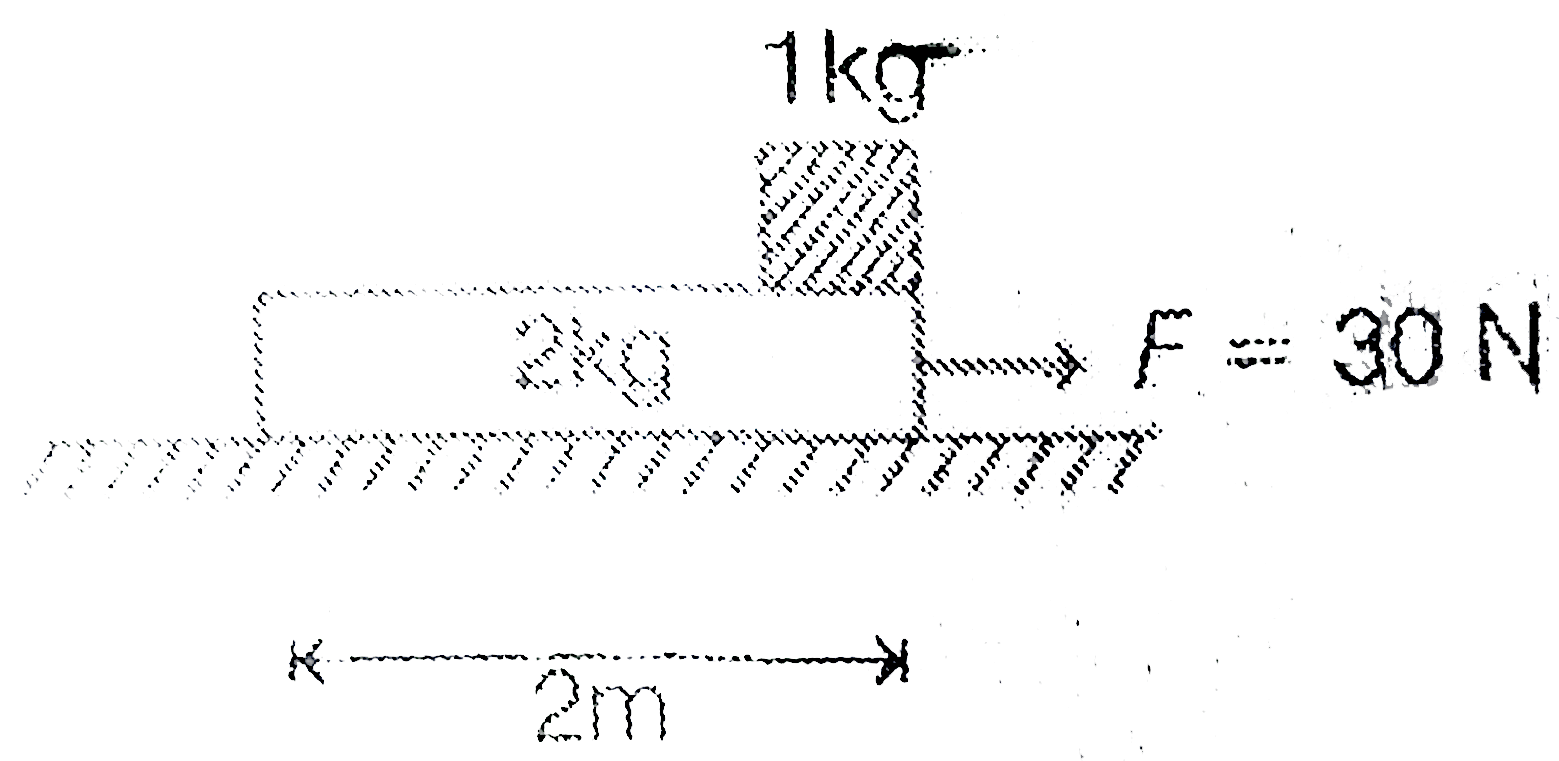
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
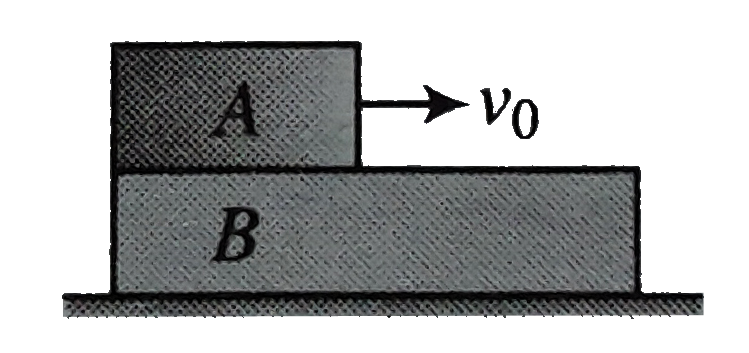
View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
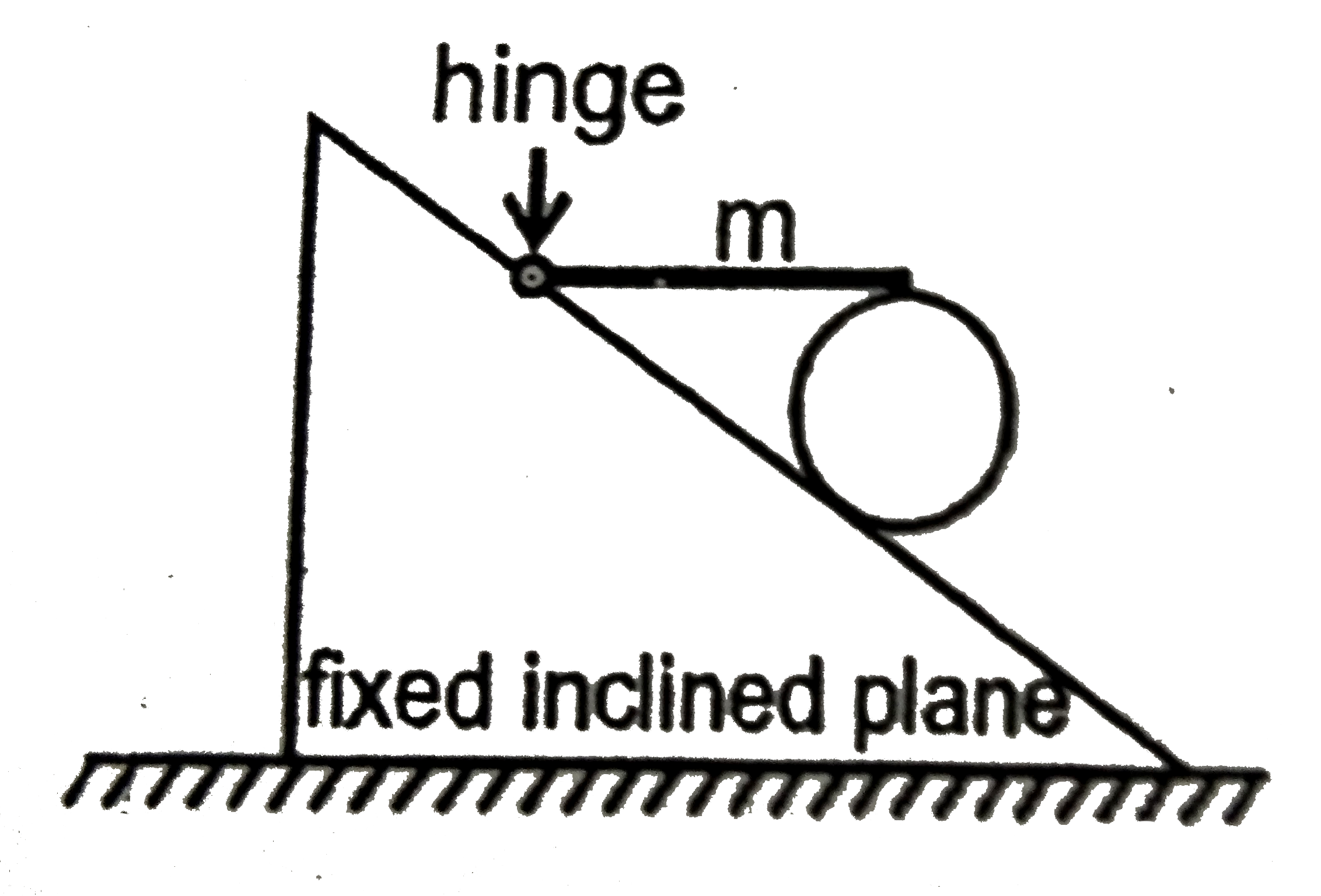
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View SolutionA cylinder of 10 kg is sliding in a plane with an initial velocity of 10 m / s . If the coefficient of friction between the surface and cylinder is 0.5 then before stopping, it will cover. (g=10m/s2)
View Solution