Two blocks A and B of masses mA and mB are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Show that the kinetic energies of the blocks are, at any instant inversely proportional to their masses.
The correct Answer is:A
To show that the kinetic energies of the blocks A and B are inversely proportional to their masses, we can follow these steps:
1. Identify the Masses: Let the mass of block A be mA and the mass of block B be mB.
2. Conservation of Momentum: Since there are no external forces acting on the system, the total momentum of the system must be conserved. If we denote the momentum of block A as pA and the momentum of block B as pB, we have:
pA+pB=0
This implies:
pA=−pB
3. Kinetic Energy Formula: The kinetic energy (KE) of an object is given by the formula:
KE=p22m
where p is the momentum and m is the mass of the object.
4. Kinetic Energy of Each Block:
- For block A:
KEA=p2A2mA
- For block B:
KEB=p2B2mB
5. Substituting Momentum: Since pA=−pB, we can denote the magnitude of the momentum as p:
|pA|=|pB|=p
Therefore, we can rewrite the kinetic energies as:
- For block A:
KEA=p22mA
- For block B:
KEB=p22mB
6. Ratio of Kinetic Energies: To show the relationship between the kinetic energies, we can take the ratio of KEA to KEB:
KEAKEB=p22mAp22mB=mBmA
7. Conclusion: This implies:
KEA∝1mAandKEB∝1mB
Thus, the kinetic energies of the blocks are inversely proportional to their masses.
pA+pB=0
This implies:
pA=−pB
KE=p22m
where p is the momentum and m is the mass of the object.
- For block A:
KEA=p2A2mA
- For block B:
KEB=p2B2mB
|pA|=|pB|=p
Therefore, we can rewrite the kinetic energies as:
- For block A:
KEA=p22mA
- For block B:
KEB=p22mB
KEAKEB=p22mAp22mB=mBmA
KEA∝1mAandKEB∝1mB
Thus, the kinetic energies of the blocks are inversely proportional to their masses.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
Two blocks A and B of masses 1kg and 2kg are connected together by means of a spring and are resting on a horizontal frictionless table. The blocks are then pulled apart so as to stretch the spring and then released. Find the ratio of their,
(a) speed
(b) magnitude of momentum and
(c) kinetic energy at any instant.
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionTwo blocks A and B of masses 3 kg and 6 kg are connected by a massless spring of force constant 1800 N m−1 and then they are placed on a smooth horizontal surface. The blocks are pulled apart to stretch the spring by 5 cm and then released. What is the relative velocity (in ms−1) of the blocks when the spring comes to its natural length?
View SolutionTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution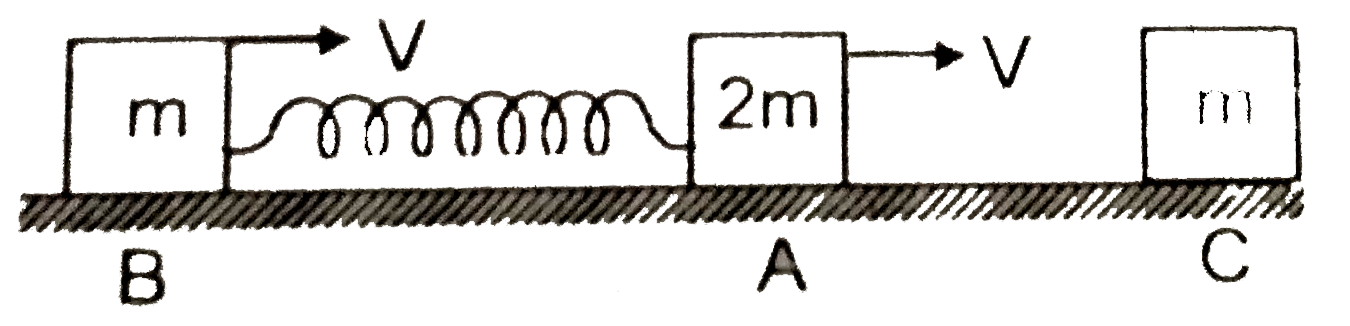
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be
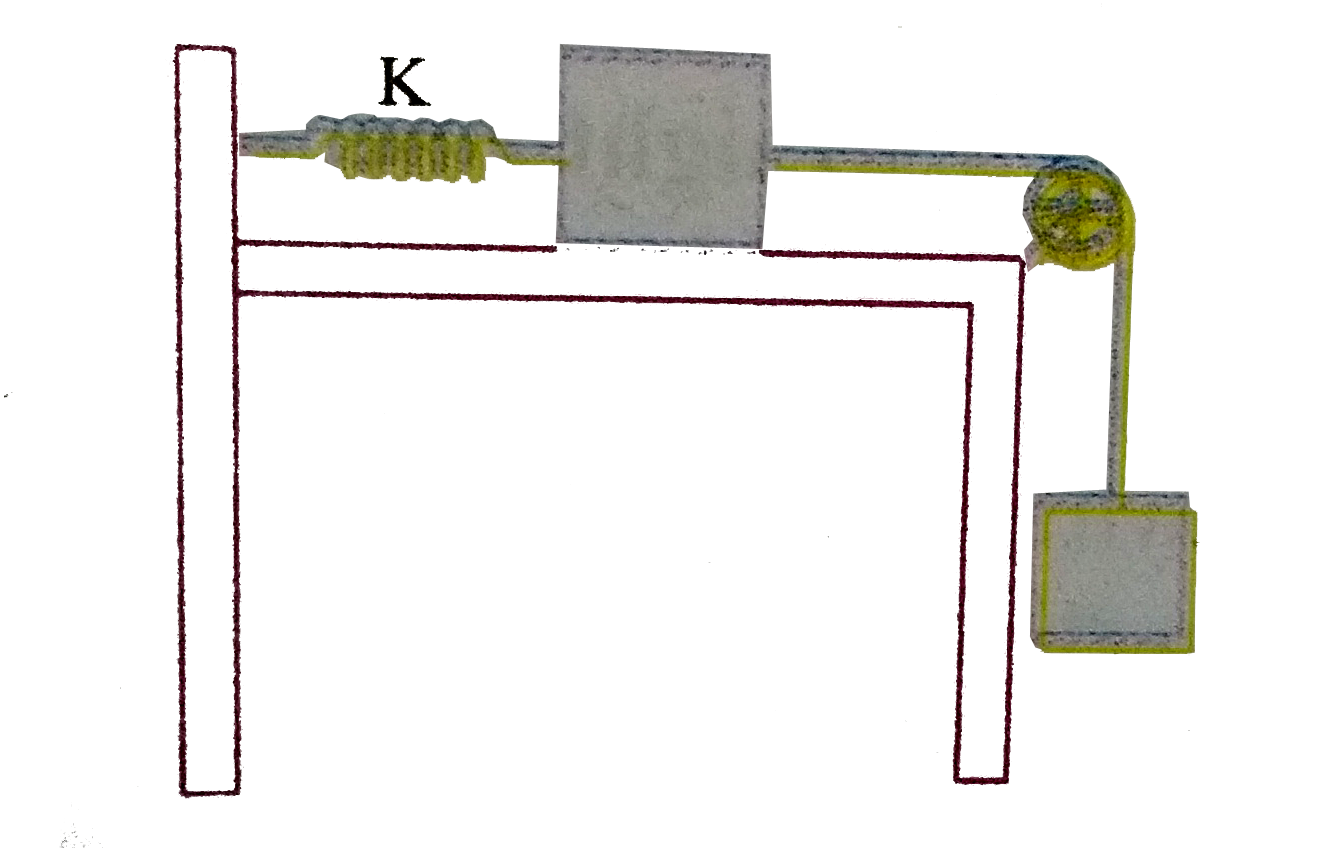
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution
