Two billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
The correct Answer is:B, C
To solve the problem, we will follow these steps:
Step 1: Understand the scenario
We have two billiard balls of the same mass m in contact on a table, and a third ball of the same mass m strikes them symmetrically. After the impact, the third ball remains at rest. We need to find the coefficient of restitution e between the balls.
Step 2: Define the initial conditions
Let:
- The initial velocity of the third ball (the one that strikes) be u.
- The two balls in contact are initially at rest.
Step 3: Analyze the collision
Since the third ball strikes the two balls symmetrically, we can conclude that the angle between the lines connecting the centers of the two balls is 60∘ (as they form an equilateral triangle).
Step 4: Apply conservation of momentum
Before the collision, the total momentum in the horizontal direction is:
pinitial=mu
After the collision, let V be the velocity of each of the two balls after the collision. The momentum of the two balls after the collision is:
pfinal=2mVcos(30∘)
Using the conservation of momentum:
mu=2mVcos(30∘)
Dividing through by m:
u=2V⋅√32
This simplifies to:
u=V√3
Thus, we find:
V=u√3
Step 5: Use the definition of the coefficient of restitution
The coefficient of restitution e is defined as:
e=Relative velocity after collisionRelative velocity before collision
The relative velocity before the collision (in the direction of the line of impact) is:
ubefore=u−0=u
The relative velocity after the collision for the two balls is:
uafter=V−0=V
Thus, we can write:
e=Vu
Step 6: Substitute the value of V
Substituting V=u√3 into the equation for e:
e=u√3u=1√3
Step 7: Final answer
The coefficient of restitution between the balls is:
e=1√3≈0.577
We have two billiard balls of the same mass m in contact on a table, and a third ball of the same mass m strikes them symmetrically. After the impact, the third ball remains at rest. We need to find the coefficient of restitution e between the balls.
Let:
- The initial velocity of the third ball (the one that strikes) be u.
- The two balls in contact are initially at rest.
Since the third ball strikes the two balls symmetrically, we can conclude that the angle between the lines connecting the centers of the two balls is 60∘ (as they form an equilateral triangle).
Before the collision, the total momentum in the horizontal direction is:
pinitial=mu
After the collision, let V be the velocity of each of the two balls after the collision. The momentum of the two balls after the collision is:
pfinal=2mVcos(30∘)
Using the conservation of momentum:
mu=2mVcos(30∘)
Dividing through by m:
u=2V⋅√32
This simplifies to:
u=V√3
Thus, we find:
V=u√3
The coefficient of restitution e is defined as:
e=Relative velocity after collisionRelative velocity before collision
The relative velocity before the collision (in the direction of the line of impact) is:
ubefore=u−0=u
The relative velocity after the collision for the two balls is:
uafter=V−0=V
Thus, we can write:
e=Vu
Substituting V=u√3 into the equation for e:
e=u√3u=1√3
The coefficient of restitution between the balls is:
e=1√3≈0.577
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Subjective Questions
Explore 1 Video
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Single Correct
Explore 23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 1 Objective
Explore 42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
Two identical billiard balls are in contact on a table. A third identical ball strikes them symmetrically and comes to rest after impact. The coefficient of restitution is :
View SolutionIf the collision of a ball of mass m is inelastic, then the relation between theta and alpha is (where theta is the coefficient of restitution)
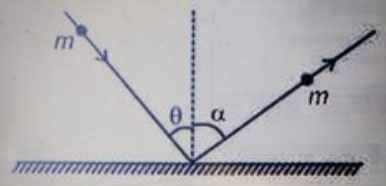
View SolutionTwo equal spheres B and C, each of mass m, are in contact on a smooth horizontal table. A third sphere A of same size as that of B or C but mass m/2 impinges symmetrically on them with a velocity u and is itself brought to rest.
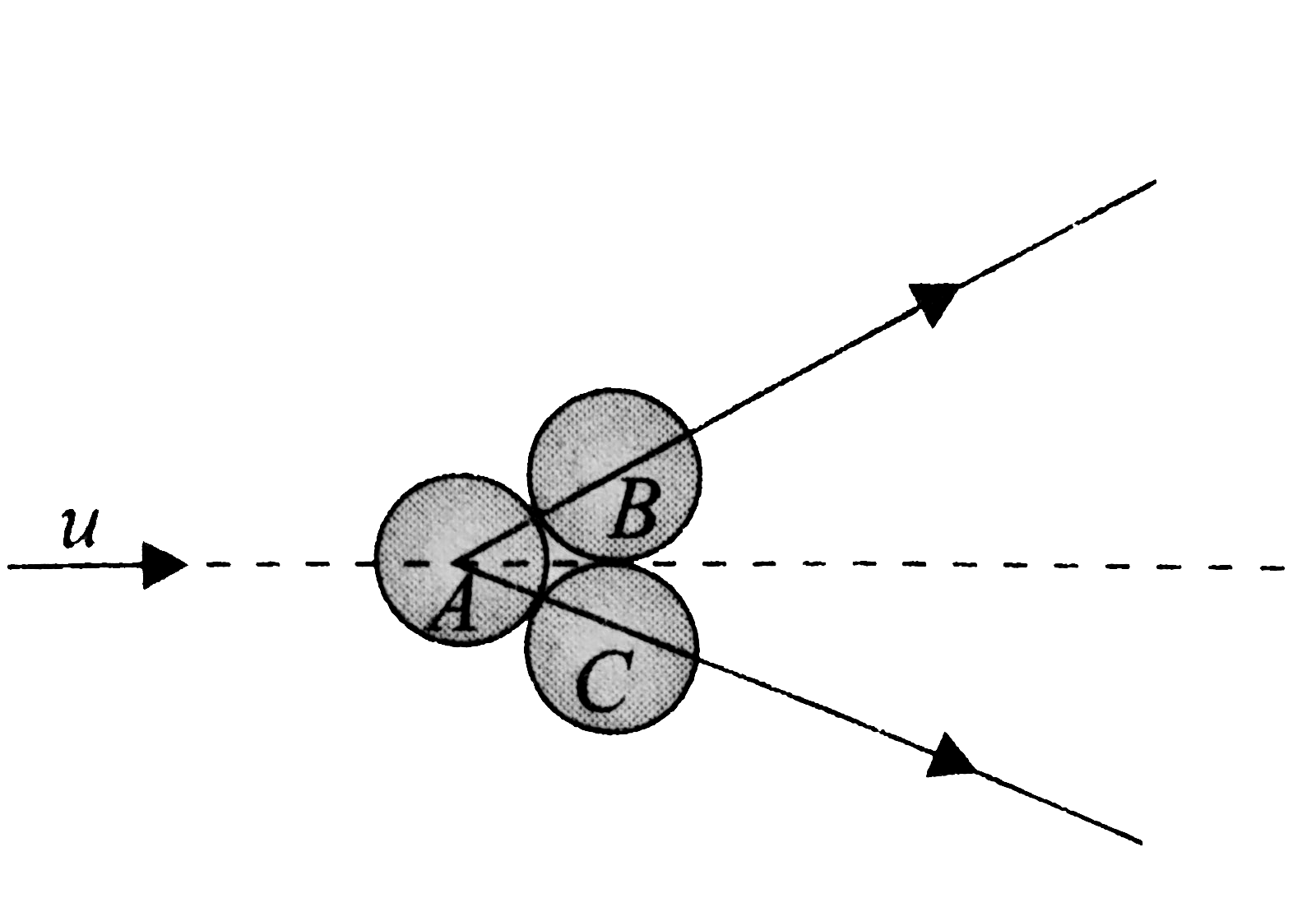
The coefficient of restitution between the two spheres A and B (or between A and C) is
View SolutionBall 1 collides directly with another identical ball 2 at rest. Velocity of second ball becomes two times that of 1 after collison. Find the coefficient of restitution between the two balls?
View SolutionBall 1 collides directly with another identical ball 2 at rest. Velocity of second ball becomes two times that of 1 after collison. Find the coefficient of restitution between the two balls?
View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
View SolutionA ball is dropped on a smooth inclined plane and is observed to move horizontally after the impact. The coefficient of restitution between the plane and ball is e. The inclination of the plane is
View SolutionA ball of negligible size and mass m is given a velocity v0 on the centre of the cart which has a mass M and is originally at rest. If the coefficient of restitution between the ball and walls A and B is e. Determine the velocity of the ball and the cart just after the ball strikes A. Also, determine the total time needed for the ball to strike A, rebound, then strike B, and rebound and then return to the centre of the cart. Neglect friction.

View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.


View Solution