A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
The correct Answer is:A, B
To solve the problem, we need to find the minimum and maximum initial speed u of a particle of mass 100 g (0.1 kg) that collides with another particle of the same mass initially at rest. After the collision, the total kinetic energy is given as 0.2 J.
1. Identify the mass of the particles:
- Mass of each particle, m=100g=0.1kg.
2. Write the expression for initial kinetic energy (KE):
- The initial kinetic energy of the moving particle is given by:
KEinitial=12mu2
- Substituting the mass:
KEinitial=12×0.1kg×u2=0.05u2
3. Set up the equation for final kinetic energy:
- The total kinetic energy after the collision is given as 0.2 J:
KEfinal=0.2J
4. Apply the conservation of kinetic energy:
- According to the conservation of kinetic energy, we have:
KEinitial=KEfinal
- Therefore, we can write:
0.05u2=0.2
5. Solve for u2:
- Rearranging the equation gives:
u2=0.20.05=4
6. Calculate the value of u:
- Taking the square root:
u=√4=2m/s
7. Determine the minimum and maximum values of u:
- Since the collision can be elastic or inelastic, the maximum value of u occurs in an elastic collision where both particles move after the collision, while the minimum value of u occurs in a perfectly inelastic collision where they stick together.
- In a perfectly inelastic collision, the final kinetic energy is less than the initial kinetic energy, but since we are given the final kinetic energy, we can conclude that the minimum and maximum value of u is:
- Minimum u=2m/s
- Maximum u=2m/s
Final Answer:
- The minimum and maximum value of u is 2m/s.
- Mass of each particle, m=100g=0.1kg.
- The initial kinetic energy of the moving particle is given by:
KEinitial=12mu2
- Substituting the mass:
KEinitial=12×0.1kg×u2=0.05u2
- The total kinetic energy after the collision is given as 0.2 J:
KEfinal=0.2J
- According to the conservation of kinetic energy, we have:
KEinitial=KEfinal
- Therefore, we can write:
0.05u2=0.2
- Rearranging the equation gives:
u2=0.20.05=4
- Taking the square root:
u=√4=2m/s
- Since the collision can be elastic or inelastic, the maximum value of u occurs in an elastic collision where both particles move after the collision, while the minimum value of u occurs in a perfectly inelastic collision where they stick together.
- In a perfectly inelastic collision, the final kinetic energy is less than the initial kinetic energy, but since we are given the final kinetic energy, we can conclude that the minimum and maximum value of u is:
- Minimum u=2m/s
- Maximum u=2m/s
- The minimum and maximum value of u is 2m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
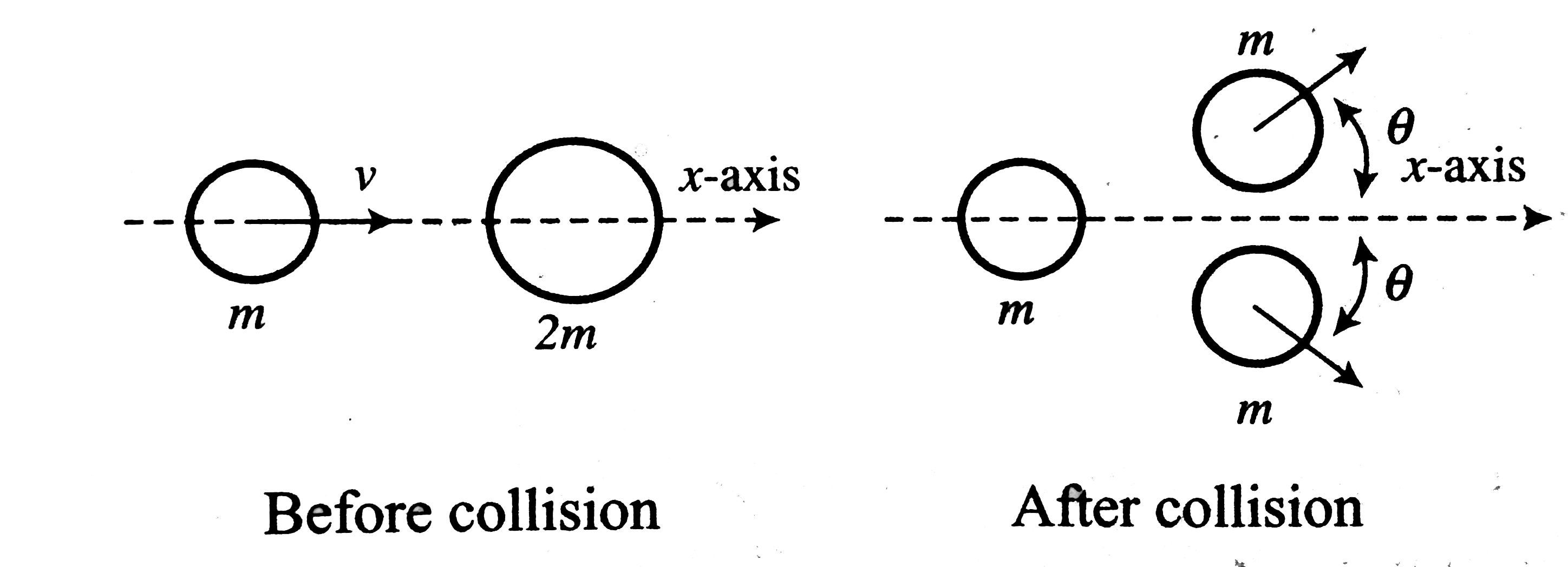
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View SolutionIf one sphere collides head - on with another sphere of the same mass at rest inelastically. The ratio of their speeds (v2v1) after collision shall be
View SolutionOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
View SolutionA body of mass 2 m moving with velocity v makes a head - on elastic collision with another body of mass m which is initially at rest. Loss of kinetic energy of the colliding body (mass 2 m) is
View Solution
