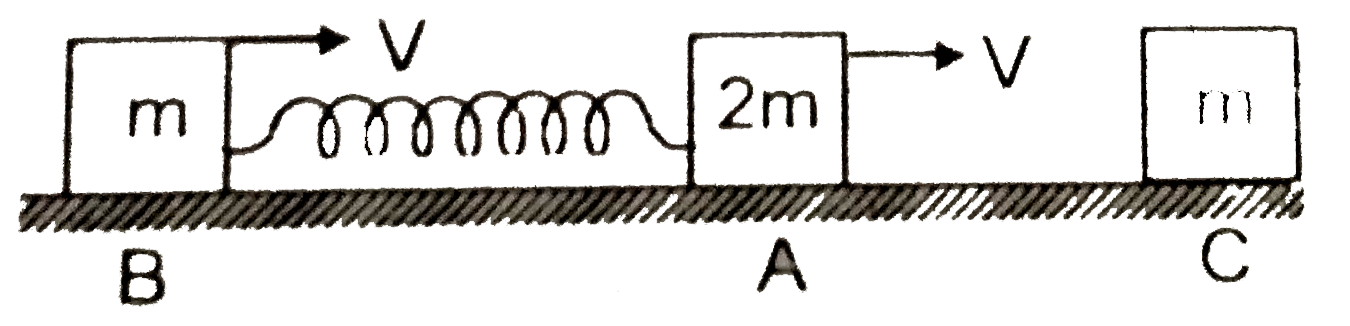
Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be

$\sqrt{\frac{3}{2} \frac{m}{k}} V$

$\sqrt{\frac{27 m}{8 K}} V$

$\sqrt{\frac{9 m}{8 K}} V$

$\sqrt{\frac{8 m}{27 K}} V$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Velocity of a after the collision withh $C, V_{1} = \frac{V}{3}$
$∴$ velocity of each block A and B at maximum compression
$V_{2} = \frac{5}{9} V$
$∴ \frac{1}{2} k x^{2} + \frac{1}{2} 3 m {(\frac{5}{9} V)}^{2}$
$= \frac{1}{2} m v^{2} + \frac{1}{2} 2 m {(\frac{V}{3})}^{2}$
$x = \sqrt{\frac{8 m}{27 K}} V$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

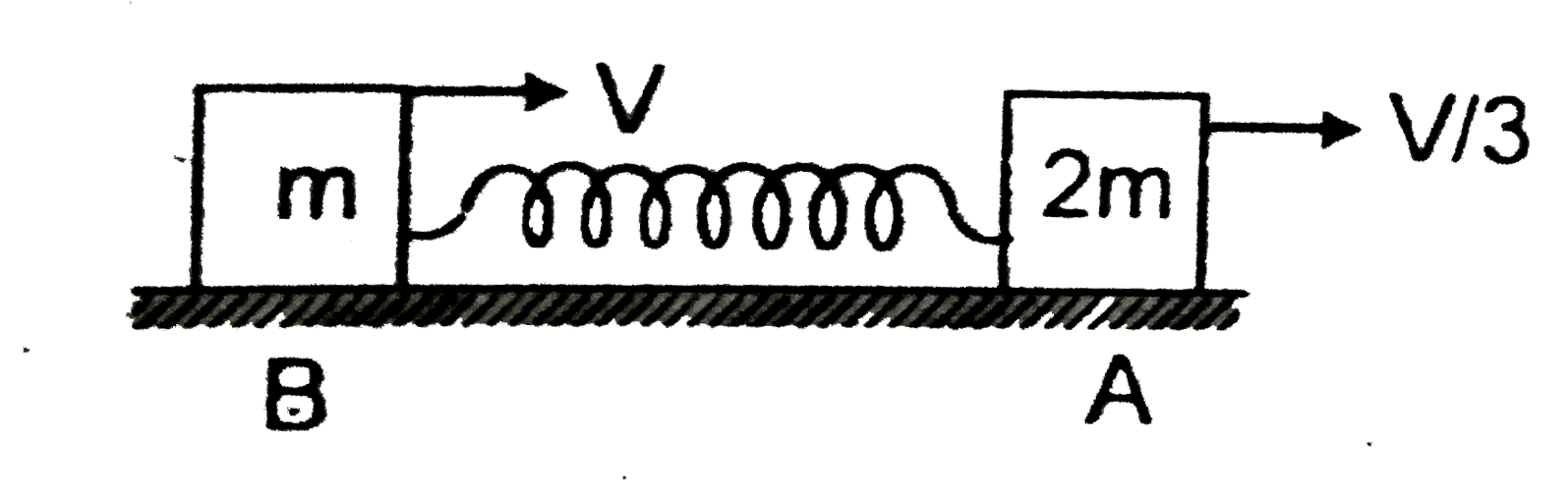
Similar Questions

Two blocks $A$ and $B$ of mass $2 m$ and $m$ respectively are connected to a massless spring of force constant $K$ as shown in figure $A$ and $B$ are moving on the horizontal frcitionless surface with velocity $v$ to right with underformed spring. If $B$ collides with $C$ elastically, then maximum compression of the spring will be

View Solution
Two blocks A and B of mass m and $2 m$ respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

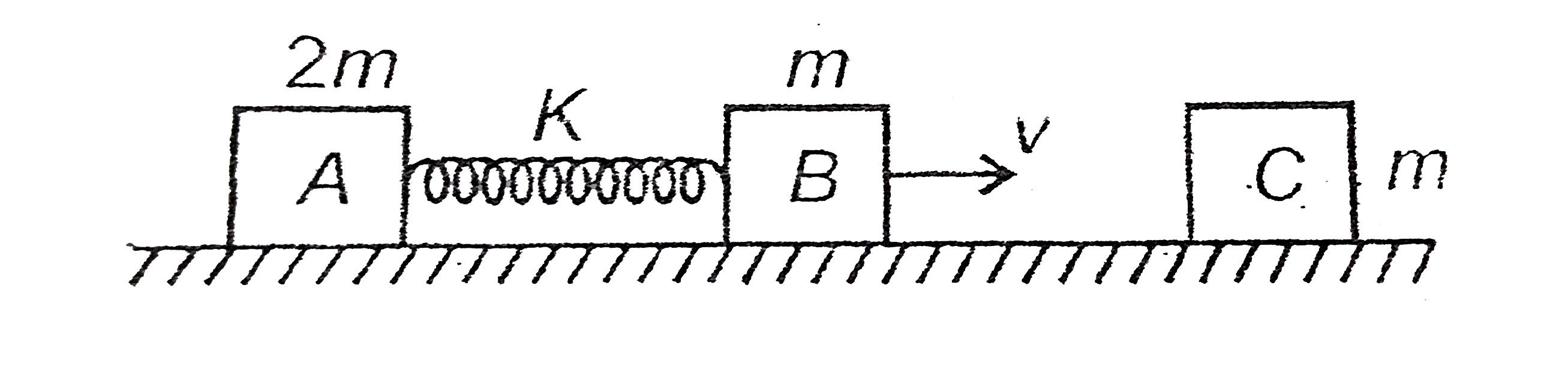
View Solution
Two block A and B of masses m and $2 m$ respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity $v_{0}$ each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass $2 m$ . at rest, the collision being completely inelastic.

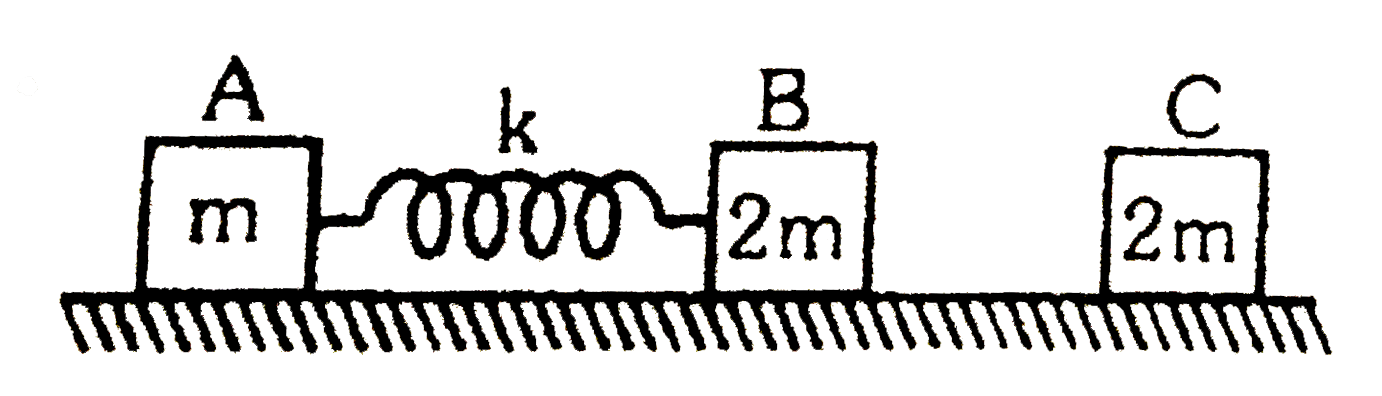
The velocity of block B just after collision is -
View Solution
Two blocks $A$ and $B$ of masses $m$ and $2 m$ , respectively are connected by a spring of force constant $k$ . The masses are moving to the right with uniform velocity $v$ each, the heavier mass leading the lighter one. The spring is in the natural length during this motion. Block $B$ collides head on with a third block $C$ of mass $m$ , at rest, the collision being completely inelastic. Calculate the maximum compression of the spring.

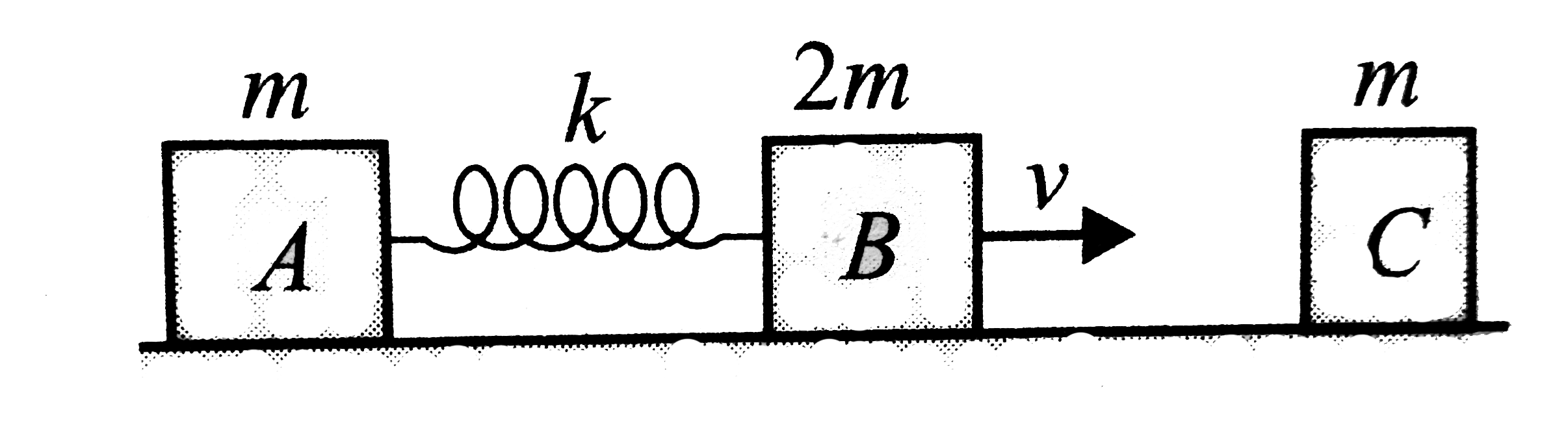View Solution
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
Two blocks of masses $m_{1} and m_{2}$ are connected by a spring of spring constant k figure. The block of mass $m_{2}$ is given a shape impulse so that it acquires a velocity $v_{0}$ towards right. Find a. the velocity of the centre of mass b. the maximum elongation that the spring will suffer.

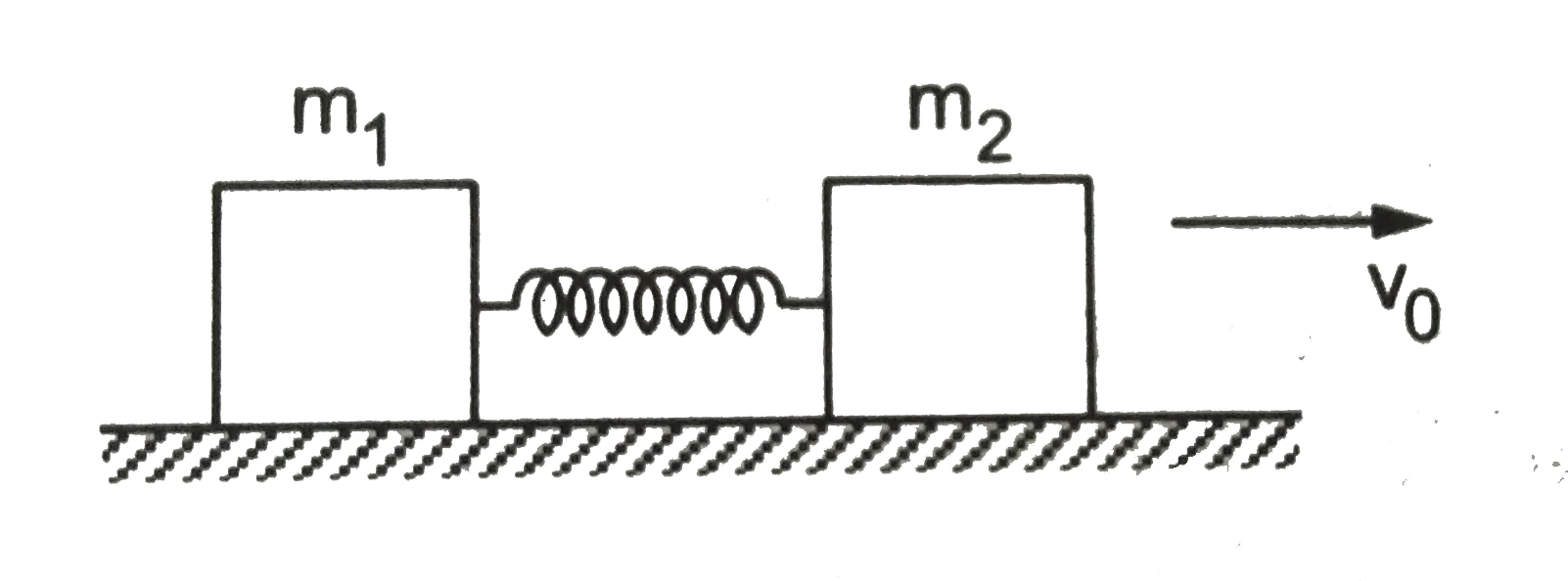View Solution
A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is $μ$ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution
Two blocks $A$ and $B$ of masses in and $2 m$ , respectively, are connected with the help of a spring having spring constant, $k$ as shown in Fig. Initially, both the blocks arc moving with same velocity $v$ on a smooth horizontal plane with the spring in its natural length. During their course of motion, block $B$ makes an inelastic collision with block $C$ of mass $m$ which is initially at rest. The coefficient of restitution for the collision is $1 / 2$ . The maximum compression in the spring is

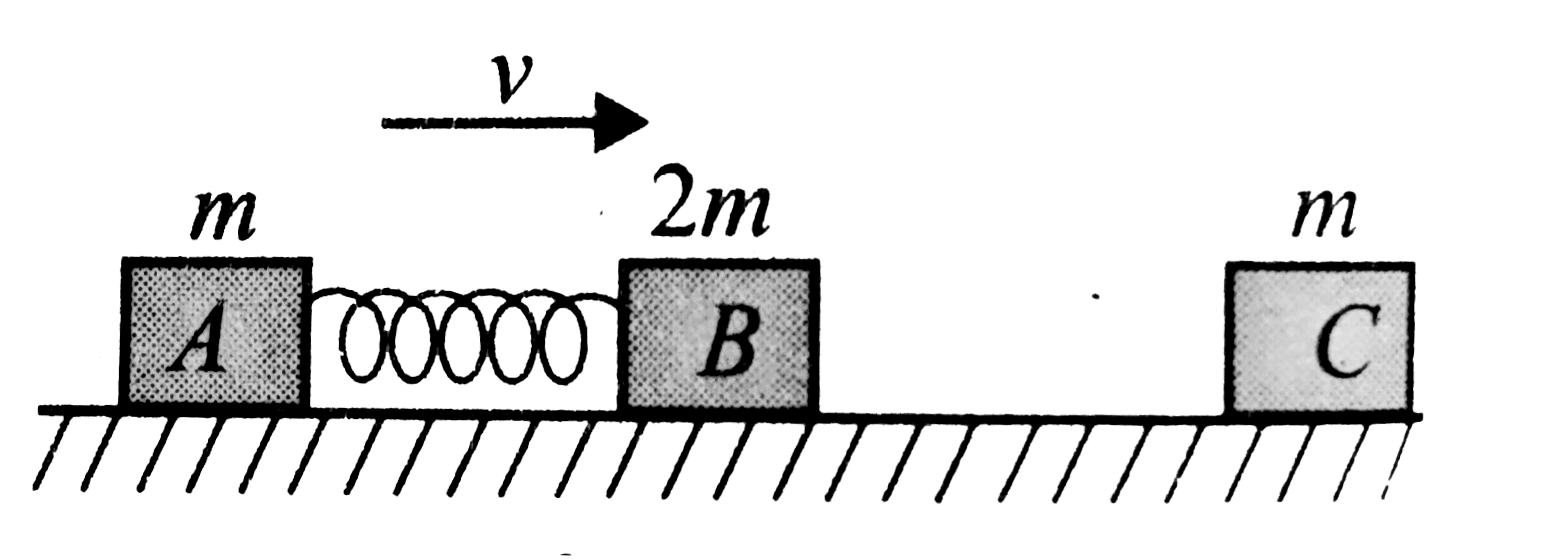View Solution
Two blocks of masses $m_{1}$ =1kg and $m_{2}$ = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block $m_{1}$ is imparted an initial velocity $v_{0}$ = 12cm/s to the right. The amplitude of oscillation is
View Solution
A body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View Solution

Two blocks A and B of mass 2 m and m respectively are connected to a massless spring of spring constant K. if A and B moving on the horizontal frictionless surface with velocity v to right. If A collides with C of mass m elastically and head on, then the maximum compressions of the spring will be

The correct Answer is:D

Velocity of a after the collision withh C,V1=V3 ∴ velocity of each block A and B at maximum compression V2=59V ∴12kx2+123m(59V)2 =12mv2+122m(V3)2 x=√8m27KV

Similar Questions

Recommended Questions