If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

μg
g(1+μ1−μ)
g(1−μ1+μ)
gμ
The correct Answer is:B
Let a= maximum acceleration of A.
Under no slip condition acceleration of B is also a
FBDofAw.r.t. ground
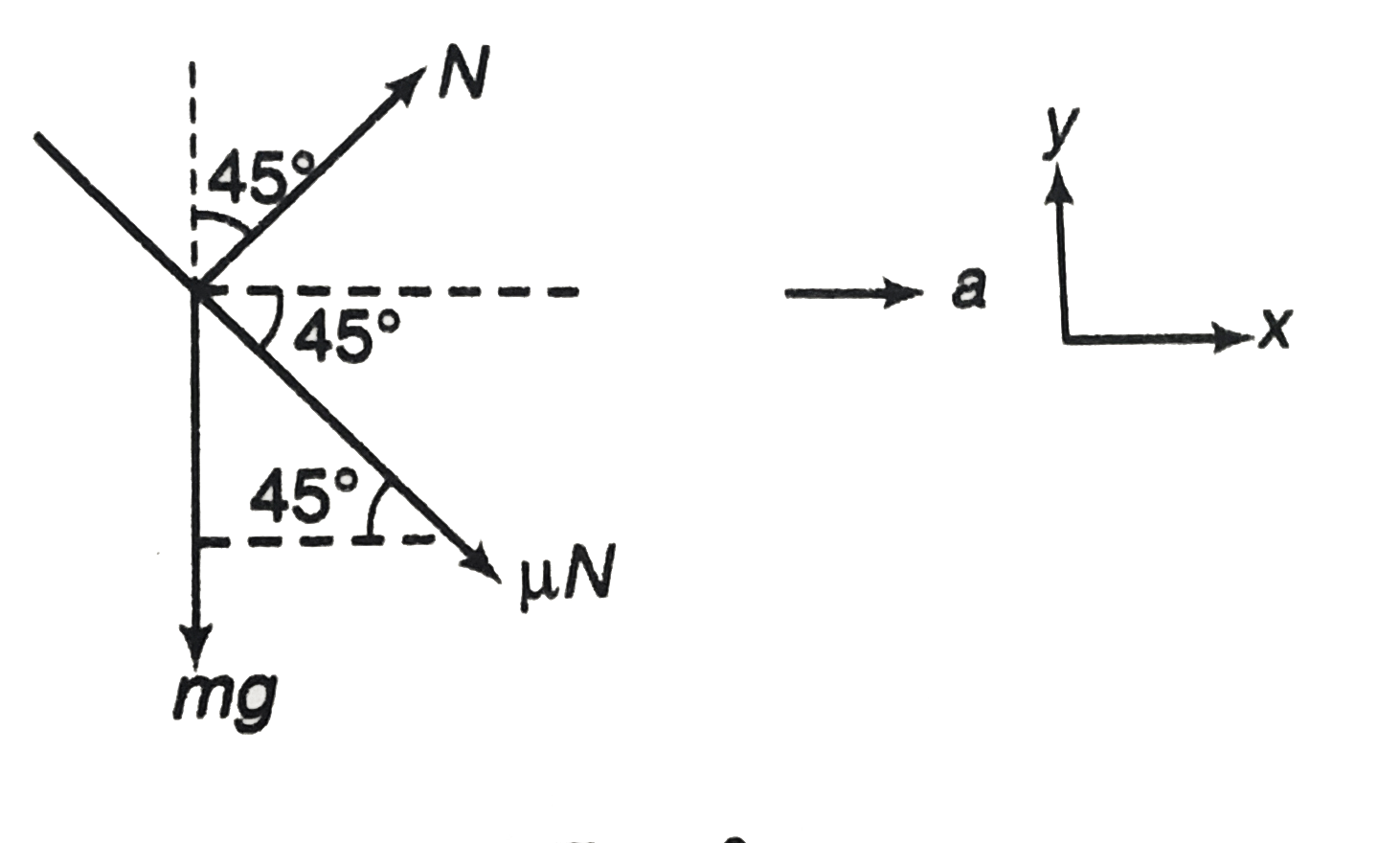
∑Fy=0
∴N√2=mg+μN√2 …(i)
∑Fx=ma
∴N√2+μN√2=ma ...(ii)
Solving these two equations, we get
a=g(1+μ1−μ)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
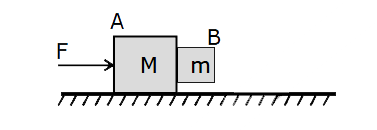
Coefficient of friction between A and B is μ . The minimum force F with which A will be pushed such that B will not slip down is -
View SolutionThe minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
View SolutionIf the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]

View Solution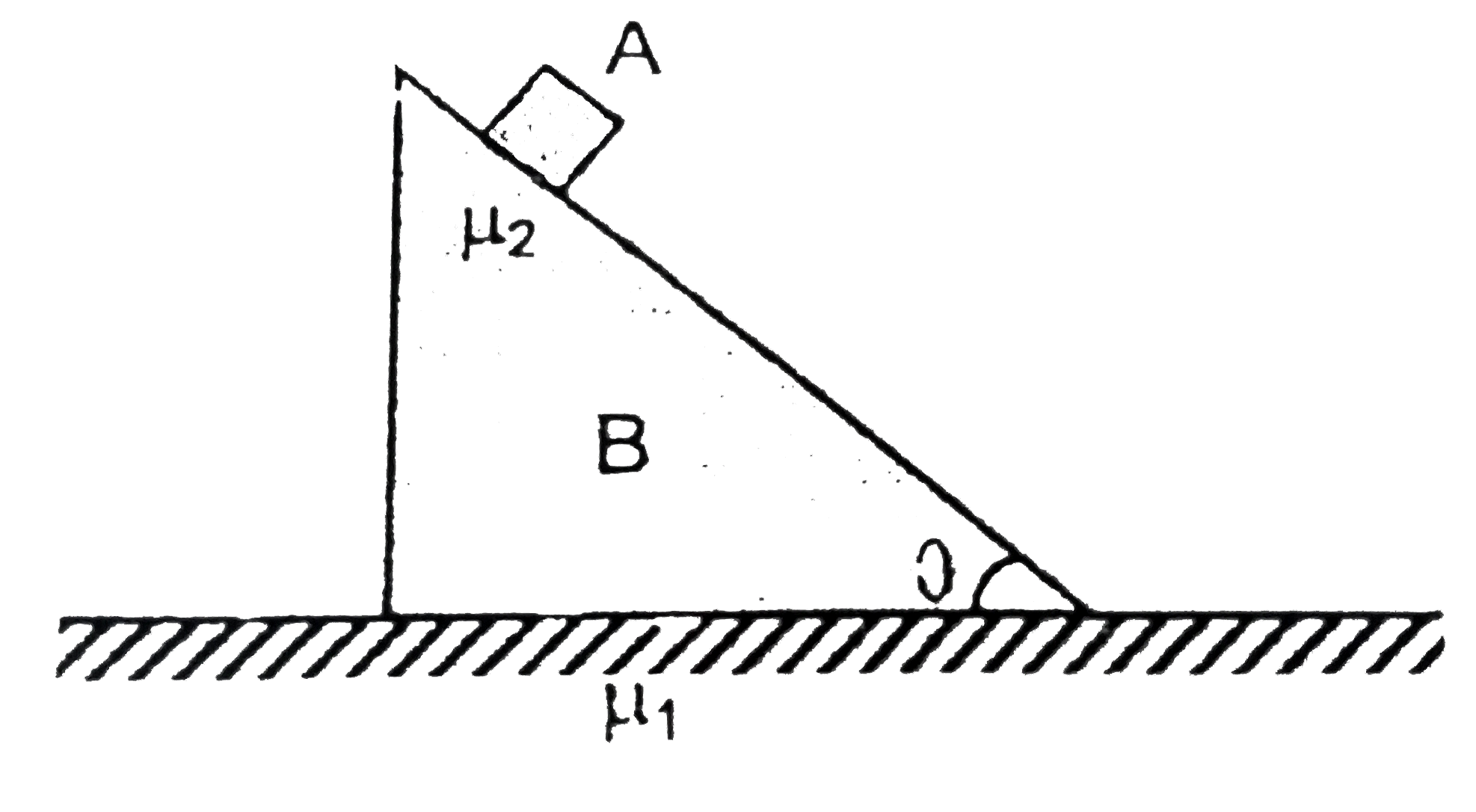
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View Solution
A wedge B of mass 2 m is placed on a rough horizontal suface. The coefficient of friction between wedge and the horizontal surface is μ1. A block of mass m is placed on wedge as shown in the figure. The coefficient of friction between block and wedge is μ2. The block and wedge are released from rest.
Q. Suppose the inclined surface of the wedge is at θ=37∘ from angle from horizontal and μ2=0 are wedge will remain in equilibrium if
View SolutionBlock B rests on surface . If the coefficient of static friction between A and B is μ=0.4. Determine the acceleration of each , if
(a) F=30N and
(b) F=250N(g=10m/s2)

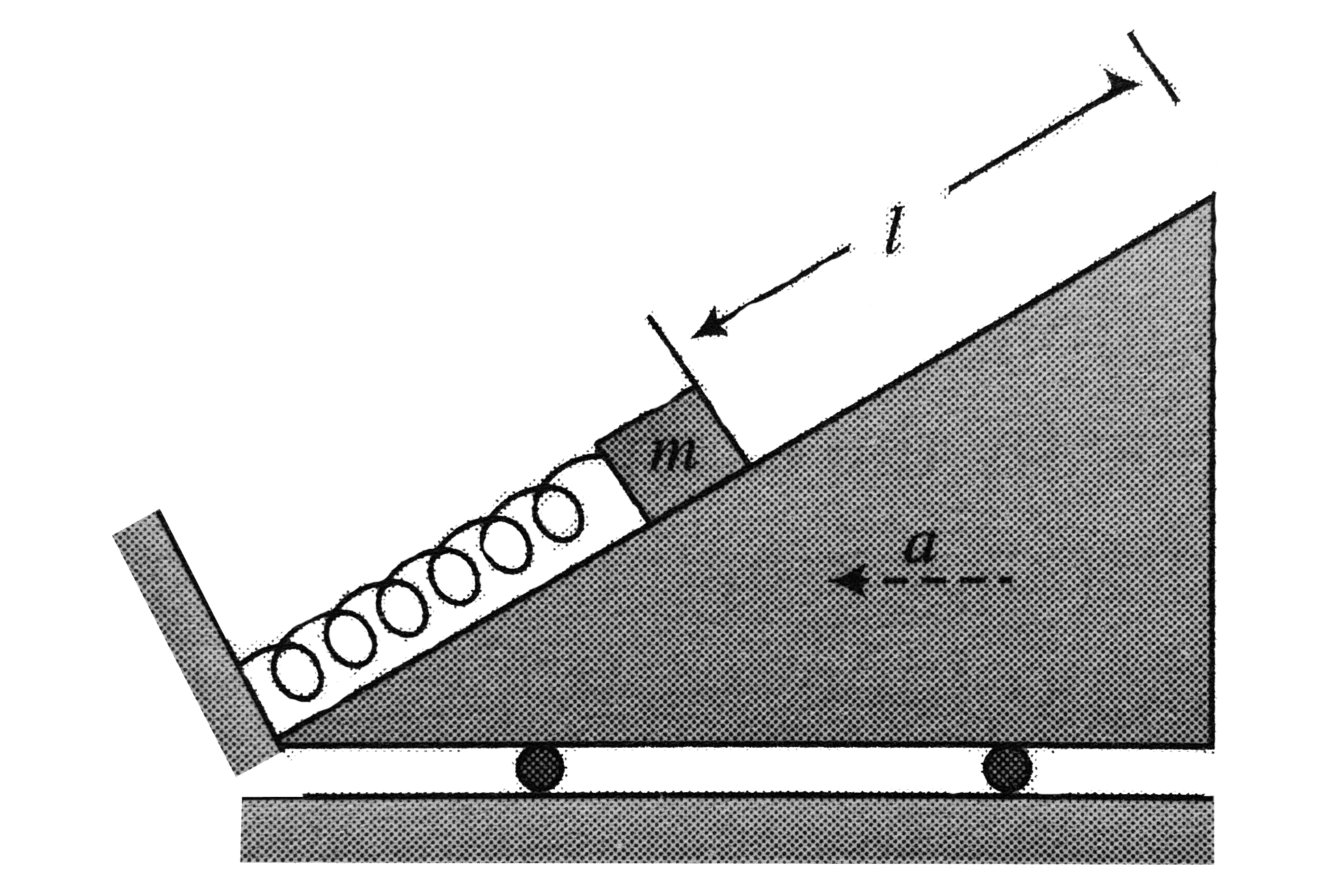
View SolutionA block of mass m is welded with a light spring of stiffness k. The spring is initially relaxed. When the wedge fitted moves with an acceleration a, as shown in figure. 8.60, the block slides through a maximum distance l relative to the wedge. If the coefficient of kinetic friction between the block and the wedges is μ, find the maximum deformation l of the spirng by using work-energy theorem.
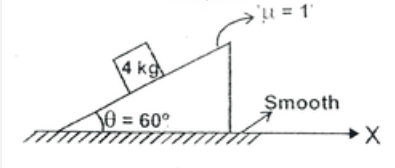
View SolutionIn the given figure the co- efficient of friction between the block and the incline plane is '1'. The acceleration with which the system should be accelerated so that the friction between the block and the wedge becomes zero ( g = 10m/s2) is
View SolutionA body B lies on a smooth horizontal table and another body A is placed on B. The coefficient of friction between A and B is μ. What acceleration given to B will cause slipping to occur between A and B
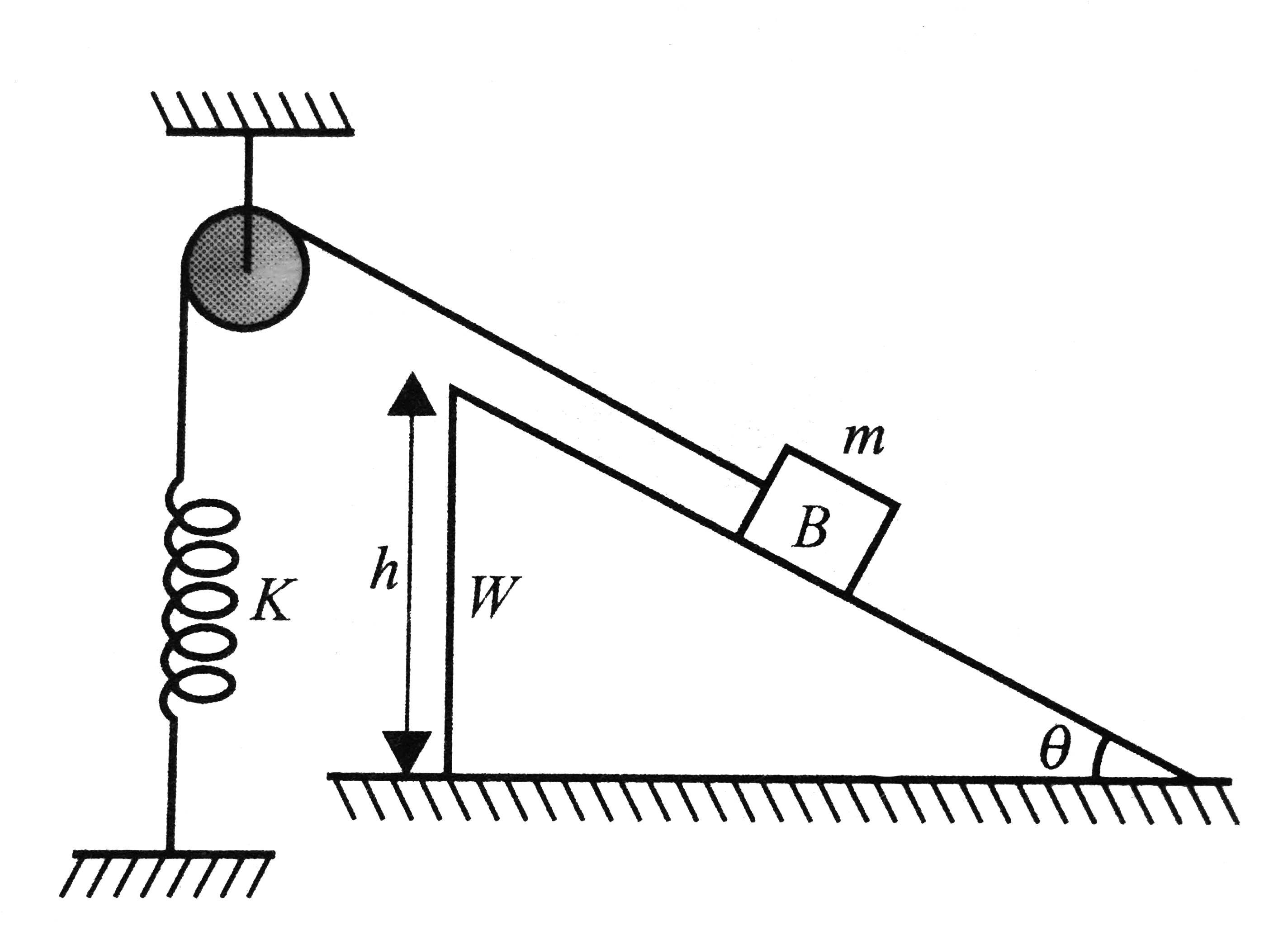
View SolutionIn figure, the pulley shown is smooth. The spring and the string are light. Block B slides down from the top along the fixed rough wedge of inclination θ. Assuming that the block reaches the end of the wedge, find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and that the spring was relaxed when the block was released from the top of the wedge.
View Solution
