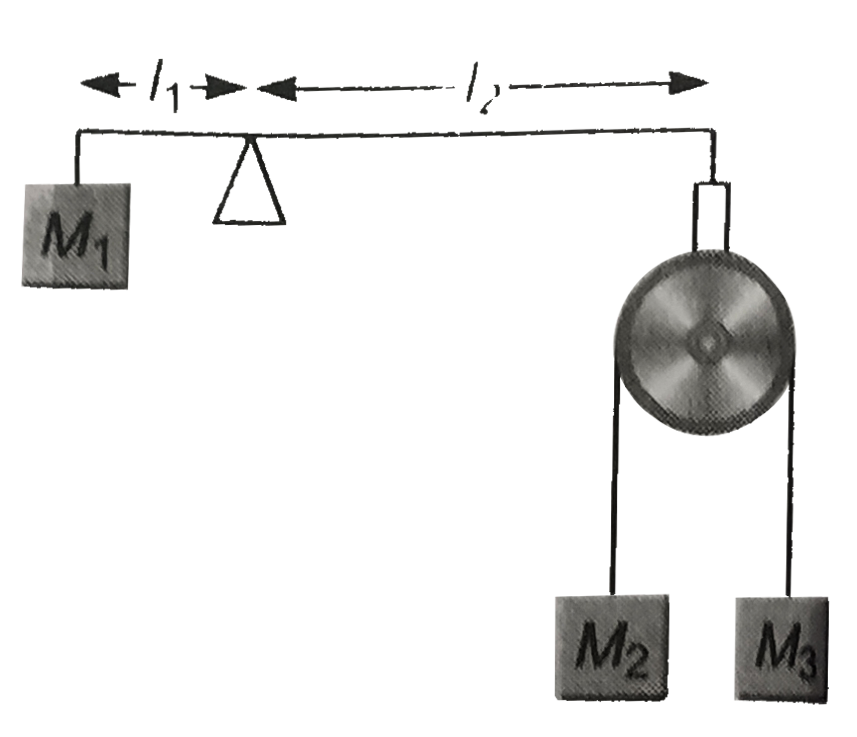
A livotad beam of negligible mass has mass suspended from one end and an Atwood's machine suspended from the other. The frictionless pulley has negligible mass and dimension. Gravity is directed downwards and , . Find the retio which will ensure that the beam has no tedency to rotate just after the masses are released.
None of these
The correct Answer is:B
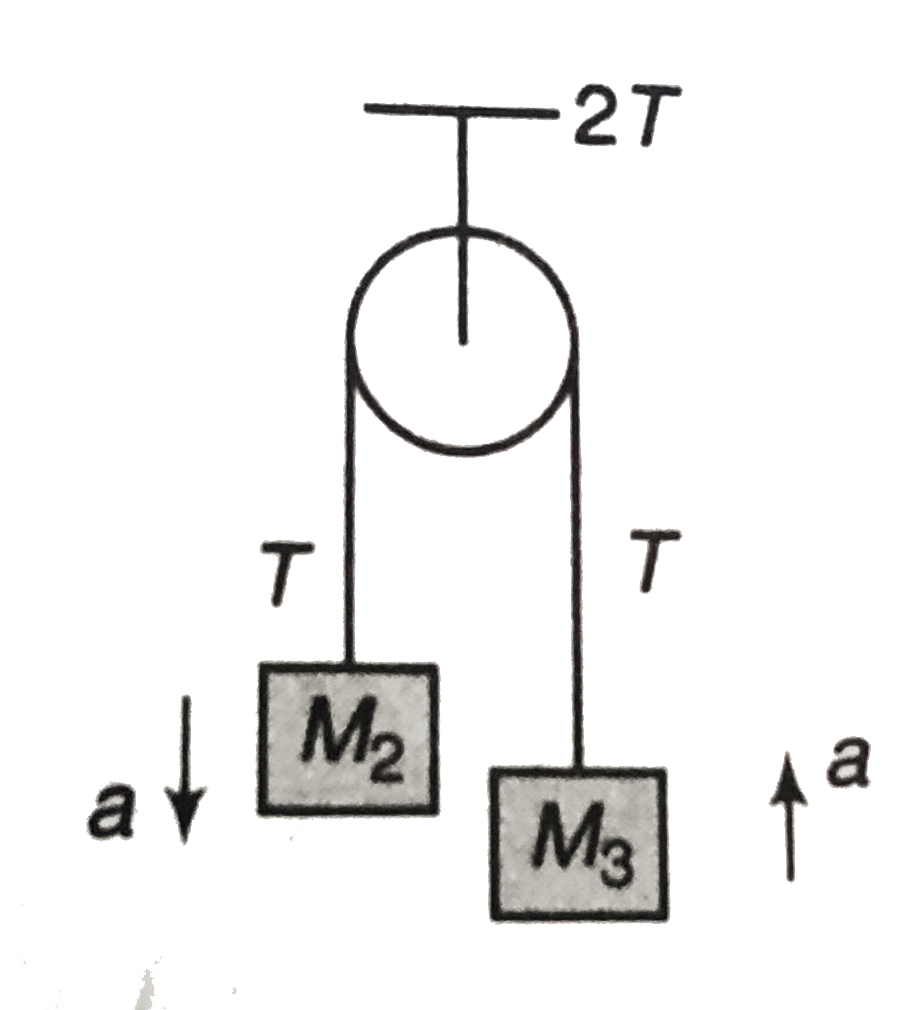
Now given the equation,
or
Now taking moment of forces about support point
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Subjective Question
Explore 27 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Single Correct
Explore 90 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
Two masses 5 kg and 3 kg are suspended from the ends of an unstretchable light string passing over a frictionless pulley. When the masses are released, the thrust on the pulley is (g = 10ms−2)
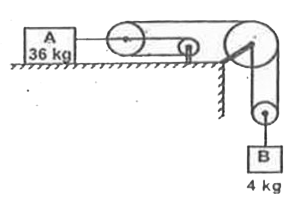
View SolutionIf the system is released from rest, determine the speeds of both masses after B has moved 1 m. Neglect friction, the masses of pulleys and inextensible string.
View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
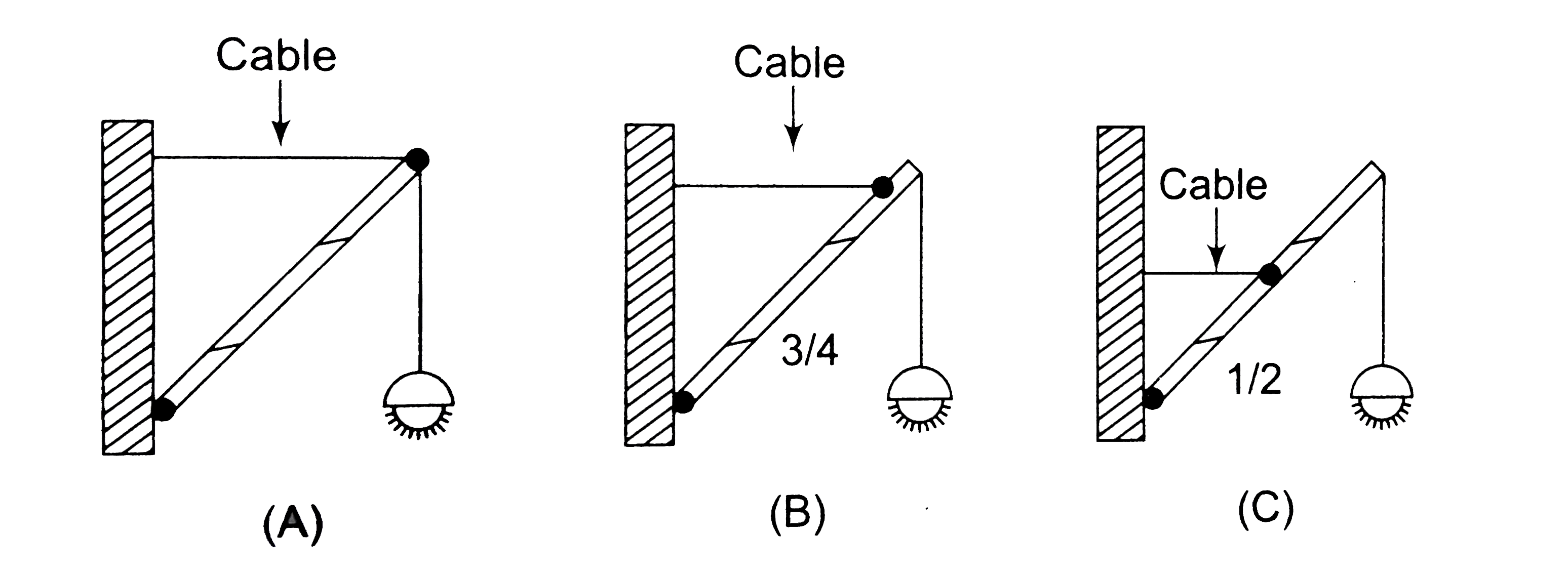
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionA light rod of length l is pivoted at distance l/4 from the left end and has two masses m0 and m attached to its ends such that rod is in equilibrium. Find m in terms of m0.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionThe period of oscillation of a mass m suspended by an ideal spring is 2s. If an additional mass of 2 kg be suspended, the time period is increased by 1s. Find the value of m.
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be
View Solution